Каким свойством обладает длина отрезка 5 класс
Инфоурок
›
Математика
›Презентации›Презентация по математике «Отрезок. Длина отрезка» 5 класс
Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
ОТРЕЗОК. ДЛИНА ОТРЕЗКА.
2 слайд

Описание слайда:
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ТОЧКА ЛИНИЯ ОТРЕЗОК ТОЧКА ОТРЕЗОК
3 слайд

Описание слайда:
Читают « Отрезок АВ» Точки А и В — концы отрезка Обозначают АВ или ВА
4 слайд

Описание слайда:
АВ = 1 см (длина отрезка АВ равна 1 см) На MN помещается три отрезка АВ MN = 3 см. На EF помещается четыре отрезка АВ EF= 4 см. РК = 17 мм Измерить отрезок означает подсчитать сколько единичных отрезков в нем помещается
5 слайд

Описание слайда:
Если на отрезке АВ отметить точку С, то длина отрезка равна сумме длин отрезков АС и СВ АВ = АС + СВ Два отрезка называют РАВНЫМИ, если они совпадают при наложении. Пишут: АВ = CD Равные отрезки имеют равные длины Длину отрезка АВ называют РАССТОЯНИЕМ между точками А и В.
6 слайд

Описание слайда:
Если конец первого отрезка совпадает с концом второго отрезка, конец второго отрезка совпадает с концом третьего отрезка и т.д., то отрезки образуют ЛОМАНУЮ Являются ли следующие фигуры ломаными? (Если нет , то почему?)
7 слайд

Описание слайда:
ЗАМКНУТЫЕ ЛОМАННЫЕ
8 слайд

Описание слайда:
Отрезок ВС на 3 см меньше отрезка АВ, длина которого равна 8 см. найдите длину отрезка АС. Задача
9 слайд

Описание слайда:
Имеем: ВС = 8 – 3 = 5 (см) АС = АВ + ВС. Отсюда АС = 8 + 5 = 13 (см) Ответ: 13 см. Решение:
10 слайд

Описание слайда:
Известно, что МК = 24 см, NP = 32 см, МР = 50 см. Найдите длину отрезка NK. Задача
11 слайд

Описание слайда:
MN = MP – NP MN = 50 – 32 = 18 (см) NK = MK – MN NK = 24 -18 = 6 (см) Ответ: 6 см. Решение:
12 слайд

Описание слайда:
Испокон веков люди пользовались такой естественной мерой длины, как шаг. Многие народы применяли меру длины дальность полета стрелы. Большие расстояния измеряли дневными переходами. Также использовали «измерительные приборы», которые были под рукой: дюйм, ладонь, пядь, локоть, фут, косая сажень и т.д. МЕРЫ ДЛИНЫ В СТАРИНУ
13 слайд

Описание слайда:
Практическая работа. Когда нет измерительного прибора, расстояние можно измерять «голыми руками». Для этого полезно знать: а) расстояние между концами большого и указательного пальцев, когда они раздвинуты; б) ширину своей ладони; в) расстояние между концами раздвинутых среднего и указательного пальцев; г) длину своего указательного пальца; д) расстояние между концами большого пальца и мизинца, когда они широко расставлены. Задание 1) Измерьте с помощью линейки размеры своей руки. 2) Измерьте рукой ширину парты. 3) Проверьте полученный результат с помощью линейки
14 слайд

Описание слайда:
? 1.Сколько существует отрезков, концами которых являются две данные точки? 2.Как обозначают отрезок? 3.Какие вы знаете единицы длины? 4.Объясните,что означает измерить длину отрезка? 5.Каким свойством обладает длина отрезка? 6.Какие отрезки называют равными? 7.Какой из двух неравных отрезков считают большим? 8.Что называют расстоянием между точками А и В? 9.Что называют длиной ломаной?
Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка — книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-806527
Вам будут интересны эти курсы:
Оставьте свой комментарий
Математика
5 класс
Урок №22
Измерение отрезков
Перечень рассматриваемых вопросов:
— понятие длины отрезка;
— равные отрезки на чертежах;
— определение длины отрезков.
Тезаурус
Длина отрезка – число, которое показывает, сколько раз в отрезке содержится единичный отрезок.
Единичный отрезок – это отрезок, длина которого принята за единицу измерения.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.
Теоретический материал для самостоятельного изучения
Каждому человеку неоднократно приходилось что-то измерять: свой рост, длину прыжка, высоту потолка и многое другое. Все эти действия означают вычисление величины какого-нибудь отрезка. Каким же образом можно измерить длину отрезка? На этот вопрос ответим в ходе урока.
За свою историю человечество придумало много разных единиц длины. Позже появились меры, заимствованные из природы:
— пядь – расстояние между растянутыми большим и указательным пальцами;
— вершок – длина основной фаланги указательного пальца;
— локоть – расстояние от локтевого сустава до конца вытянутого среднего пальца руки.
Некоторые названия сохранились до сих пор: ярд, фут, пядь, дюйм.
Ну, а герои одного известного мультфильма измеряли длину удава в попугаях. В зависимости от того, в ком измеряли удава, он становился то длиннее, то короче.
Два слонёнка, пять мартышек или тридцать восемь попугаев.
«А в попугаях я гораздо длиннее!» – воскликнул удав.
На самом деле мы с вами понимаем, что его размеры не менялись. Тогда возникает вопрос: в чём измерять? Что брать за единицу длины? Слонёнка, попугая или мартышку.
Измерить длину какого-нибудь отрезка в заданных единицах измерения – значит найти число, показывающее, сколько единичных отрезков поместится в данном отрезке.
Длиной отрезка называют число, которое показывает, сколько раз в отрезке содержится единица измерения.
Отрезок, длина которого принята за единицу измерения, называется единичным отрезком.
Чем же можно измерить длину отрезка?
Наиболее древними геометрическими инструментами являются линейка и циркуль, последний был изобретён в первом веке в Древней Греции.
Для более точных измерений используют миллиметровую линейку и штангенциркуль.
Если при измерении линейкой определённого отрезка какая-то точка не совпадает с делением шкалы, то можно говорить о приближенном значении длины этого отрезка. Приближенное значение длины может быть с избытком, с недостатком и с округлением. Например, на рисунке отрезок АВ может быть измерен с точностью до сантиметров. Его длину можно найти приближенно с избытком или с недостатком. В таких случаях говорят, что с недостатком его длина равна 5 см, а с избытком — 6 см. Это записывают так: АВ 5 см (с недостатком); АВ 6 см (с избытком).
Далее построим отрезок ВК заданной длины –например, 8см. Для этого отметим точку В и приложим к ней линейку, совместив точку В с нулём. Затем отмеряем с помощью линейки 8 см, отмечаем точку К и соединяем обе точки линией.

Такой отрезок можно построить и с помощью циркуля. Для этого отметим точку В. Приложим к линейке циркуль, выставив его ножки на восемь сантиметров. Перенесём циркуль к точке В, поместив на неё одну ножку, а другой ножкой поставим точку К. Соединив обе точки линией, получим отрезок с длиной 8 см.
Отрезки можно сравнить с помощью измерителя –например, циркуля. Для этого попеременно подставляем ножки циркуля ко всем предложенным для сравнения отрезкам. При этом они должны быть выставлены по одному из отрезков. Если длины отрезков одинаковы, то отрезки считают равными и пишут CD = КМ.
Если один из отрезков является частью другого, следовательно, он короче. Например, ЕН короче EF, так как отрезок EH является частью EF.

Рассмотрим ещё одно свойство длин.
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ. Пишут: АВ = АС + СВ.
Наши органы чувств – это один из способов получения информации об окружающем нас мире, но информация полученная таким образом, бывает искажена.
Посмотрите на рисунки и ответьте на вопрос, равны ли отрезки?
На первый взгляд покажется, что правый отрезок больше, чем левый, но при сравнении с помощью линейки окажется, что отрезки равны.

Такая же ситуация, складывается и со следующей картинкой. Кажется, что нижний отрезок больше, чем верхний, но при наложении линейки окажется, что отрезки равны.

В другом же случае на тот же вопрос о равенстве отрезков ответ очевиден.
АВ
СК
Таким образом, можно сделать вывод, что глазомерные оценки геометрических реальных величин неточны.
Разбор решения заданий тренировочного модуля
№1. Тип задания: выбор элемента из выпадающего списка.
Сравните длины горизонтального и вертикального отрезков?

- Отрезки равны
- Вертикальный отрезок больше
- Горизонтальный отрезок больше
Правильный ответ: при выполнении данного задания нужно использовать линейку, нужно измерить длину каждого отрезка и сравнить их. В результате измерений мы увидим, что отрезки равны.
№2. Тип задания: выделение цветом.
Точка К расположена на прямой между точками А и В. Длина отрезка АК = 8 см, длина отрезка КВ на 2 см больше длины отрезка АК. Какова длина отрезка АВ?
Выберите правильный ответ: 6 см; 10 см; 12 см; 18 см.
Решение: изобразим условие задачи на рисунке.

АВ = АК + КВ. Найдём КВ по условию задачи.
КВ = 8 см + 2 см = 10 см.
Следовательно, АВ = 8 см + 10 см = 18 см.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
- Сколько существует отрезков, концами которых являются две данные точки? — существует только один отрезок, концами которого являются две данные точки.
- Как обозначают отрезок? — записывают точки, которые являются концами отрезка, например: АВ, МК и т.д.
- Какие вы знаете единицы длины? — 1 мм (миллиметр), 1 дм (дециметр), 1 см (сантиметр), 1 м (метр), 1 км (километр).
- Объясните, что означает измерить длину отрезка — это означает, что надо посчитать сколько единичных отрезков (единиц длинны) помещается в этом отрезке, например, сколько раз в нём помещается один сантиметр.
- Каким свойством обладает длина отрезка? — если на отрезке АВ отметить точку С, то длина отрезка АВ будет равна сумме длин отрезков АС и СВ: АВ = АС + СВ.
- Какие отрезки называют равными? — два отрезка называют равными, если они совпадают при наложении.
- Какие длины имеют равные отрезки? — равные отрезки имеют равные длины.
- Какой из двух неравных отрезков считают большим? — большим считают тот, у которого длина больше.
- Что называют расстоянием между точками A и B? — длиной отрезка АВ.
- Объясните, какую геометрическую фигуру называют ломаной — это фигура, состоящая из последовательно соединённых отрезков и в которой конец первого отрезка совпадает с началом второго, конец второго отрезка совпадает с началом третьего и т.д.
- Что называют длиной ломаной? — сумму длин всех его звеньев (отрезков, из которых состоит ломанная.
- Какую ломаную называют замкнутой? — замкнутой называют ломанную, конец последнего отрезка которой совпадает с началом первого отрезка.
Решаем устно
1. Реши:
- Какое число больше числа 46 на 9? 46 + 9 = 55 — ответ 55
- Какое число меньше числа 72 на 15? 72 — 15 = 57 — ответ 57
- Какое число больше числа 21 в 7 раз? 21 • 7 = 147 — ответ 147
- Какое число меньше числа 65 в 13 раз? 65 : 13 = 5 — ответ 5
2. Назовите все двузначные числа, сумма цифр которых равна 6.
60, 51, 15, 42, 24, 33
3. Назовите все двузначные числа, разность цифр которых равна 7.
70, 81, 18, 92, 29
4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырёхзначное число.
9 999, 10 000, 10 001
5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырёхзначное число.
998, 999, 1 000
6. Выразите в сантиметрах:
- 7 дм 4 см = 74 см
- 4 м 1 см = 401 см
- 2 м 6 дм = 260 см
- 1 м 2 дм 5 см = 125 см
7. Выразите в дециметрах и сантиметрах:
- 72 см = 7 дм 2 см
- 146 см = 14 дм 6 см
- 450 мм = 4 дм 5 см
- 8 м 40 мм = 80 дм 4 см
Упражнения
44. Запишите все отрезки, изображённые на рисунке 15.
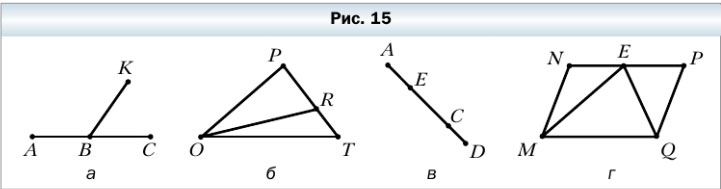
а) AB, BC, AC, BK
б) OP, PR, RT, PT, TO, OR
в) AE, AC, AD, EC, ED, CD
г) MN, NE, NP, EP, PQ, QE, QM, EM
45. Запишите все отрезки, изображённые на рисунке 16.

а) BO, BD, OD, CO, CA, OA, AD
б) FK, FE, KE, EN, ES, NS, MK, MN, MP, KN, KP, NP
46. Отметьте в тетради точки А, В, С, D и соедините их попарно отрезками. Сколько отрезков образовалось? Сколько образовалось отрезков с концом в точке A?

- Образовалось 6 отрезков с концами в данных точках: AB, AC, AD, BC, BD, CD.
- Образовалось 3 отрезка с концом в точке А: AB, AC, AD.
Комментарий: новую точку на чертеже, образованную пересечением отрезков AC и BD мы не учитываем, поскольку о ней не говорится в задании.
Для того, чтобы образование 6 отрезков выглядело более наглядно, можно расположить заданные точки в следующем порядке:

Такое решение задания также является правильным.
47. Начертите отрезки MN и АС так, чтобы MN = 6 см 3 мм, АС = 5 см 4 мм.

48. Начертите отрезки EF и ВК так, чтобы EF = 9 см 2 мм, ВК = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрезка АС?

50. Начертите отрезок ТР, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

TP — TE = 7 см 8 мм — 2 см 6 мм = 5 см 2 мм
Ответ: 5 см 2 мм.
51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.
Глядя на рисунок 17 кажется, что отрезок CD > AB.
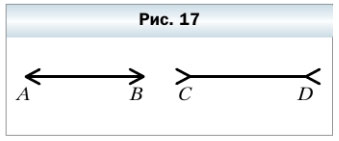
Проверим вывод измерением:
Отрезок CD = AB
Ответ: эти отрезки равны.
52. Назовите все ломаные, изображённые на рисунке 11. Какая из них имеет наибольшее количество звеньев?
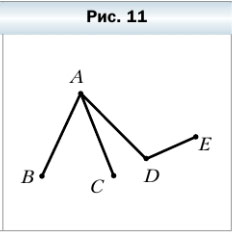
На рисунке 11 можно выделить 5 ломаных:
- BAC — 2 звена
- BADE — 3 звена
- ADE — 2 звена
- CADE — 3 звена
- CAD — 2 звена
Значит наибольшее количество звеньев имеют ломанные BADE и CADE.
53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

Назовём звенья ломанной и измерим их длину:
- AB = 19 мм
- BE = 18 мм
- EK = 16 мм
- KP = 11 мм
- PR = 12 мм
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
AB + BE + EK + KP + PR = 19 + 18 + 16 + 11 + 12 = 76 (мм) — длина ломаной ABEKPR
Ответ: длина ломаной 76 мм.
54. Запишите звенья ломаной, изображённой на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
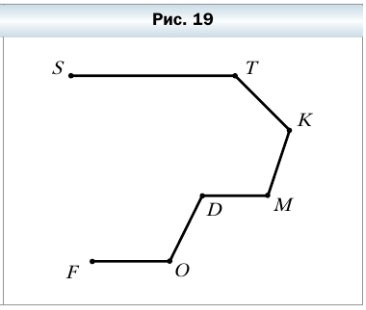
Назовём звенья ломанной и измерим их длину:
- ST = 27 мм
- TK = 13 мм
- KM = 11 мм
- MD = 11 мм
- DO = 12 мм
- OF = 13 мм
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
ST + TK + KM + MD + DO + OF = 27 + 13 + 11 + 11 + 12 + 13= 87 (мм) — длина ломаной STKMDOF
Ответ: длина ломаной 87 мм.
55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клетки правее и на 1 клетку выше точки В; точку D — на 3 клетки правее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки А, В, С, D и Е. Какая фигура образовалась? Запишите её название и укажите количество звеньев.

Образовалась фигура ломаная ABCDE. Она состоит из 4 звеньев.
56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
AB + BC + CD + DE = 8 + 14 + 23 + 10 = 55 (см) — длина ломаной ABCDE.
Ответ: длина ломаной 55 см.
57. Вычислите длину ломаной MNKPEF, если MN= 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
MN + NK + KP + PE + EF = 42 + 38 + 19 + 12 + 29 = 140 (мм) — длина ломаной MNKPEF.
Ответ: длина ломаной 55 см.
58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.

Измерим длины звеньев ломаной:
- AB = 18 мм
- BC = 30 мм
- CD = 36 мм
AB + BC + CD = 18 + 30 + 36 = 84 (мм) — длина ломаной ABCD
Ответ: длина ломаной 84 мм.
59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.

1) SK = RS • 3
34 • 3 = 102 (см) — длина отрезка SK.
2) RK = RS + SK
34 + 102 = 136 (см) — длина отрезка RK.
Ответ: длина отрезка RK 136 см.
60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если AD = 135 см.

1) DB = AD : 5
135 : 5 = 27 (см) — длина отрезка DB.
2) AB = AD + DB
135 + 27 = 162 (см) — длина отрезка АВ.
Ответ: длина отрезка АВ 162 см.
61. Известно, что АС = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.
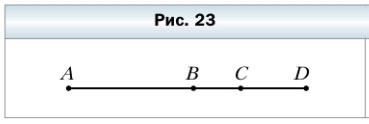
1) AB = AC — BC
32 — 9 = 23 (см) — длина отрезка AB.
2) BD = BC + CD
9 + 12 = 21 (см) — длина отрезка BD.
Ответ: AB = 23 см, BD = 21 см.
62. Известно, что MF= 43 см, ME = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.

1) MK = ME — KE
26 — 18 = 8 (см) — длина отрезка MK.
2) EF = MF — ME
43 — 26 = 17 (см) — длина отрезка EF.
Ответ: MK = 8 см, EF = 17 см.
63. Даны две точки А и В. Сколько можно провести отрезков, соединяющих эти точки? Сколько можно провести ломаных, соединяющих эти точки?
- Через две данные точки А и В можно провести один и только один отрезок, соединяющий эти точки.
- Через две данные точки А и В можно провести бесконечное количество ломанных, соединяющих эти точки.
64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

На рисунке образовались отрезки: MA, MC, MK, AC, AK, CK. Всего 6 отрезков.
65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому отрезку, причём точка К лежит между точками М и В, AM = 12 см, ВК = 9 см. Найдите длину отрезка МК.

MK = AB — (AM + KB)
28 — (12 + 9) = 28 — 21 = 7 (см) — длина отрезка MK.
Ответ: MK = 7 см.
66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрезка ВС? Есть ли в условии задачи лишние данные?

BC = AB — AC.
Так как по условию задачи АВ на 5 см больше отрезка АС, то есть AB — AC = 5 см, то BC = 5 см.
Фраза «длина отрезка АС равна 15 см» является лишней в условии задачи, поскольку длина отрезка BC будет равна 5 см независимо от значения длины отрезка АС.
Ответ: 5 см, да «длина отрезка АС равна 15 см» — лишние данные.
67. Отрезки MT и FK равны (рис. 25). Сравните отрезки MF и ТК.

MT = MF + FT
FK = FT + TK
По условию MT = FK. Значит можно записать уравнение:
MF + FT = FT + TK
MF + FT — FT = TK
MF = TK
Ответ: MF = TK
68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.

ACDM = АС + CD + DM
15 + 24 + 32 = 71 (мм) — длина ломаной ACDM.
Ответ: 71 мм.
69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.
СE = 8 мм
EF = 8 + 14 = 22 мм
FK = 22 — 7 = 15 мм

CEFK = CE + EF + FK
8 + 22 + 15 = 45 (мм) — длина ломаной CEFK.
Ответ: 45 мм.
70. Вычислите длину ломаной, изображённой на рисунке 26.
Разделим ломаные на единичные отрезки равные заданному и посчитаем их количество.
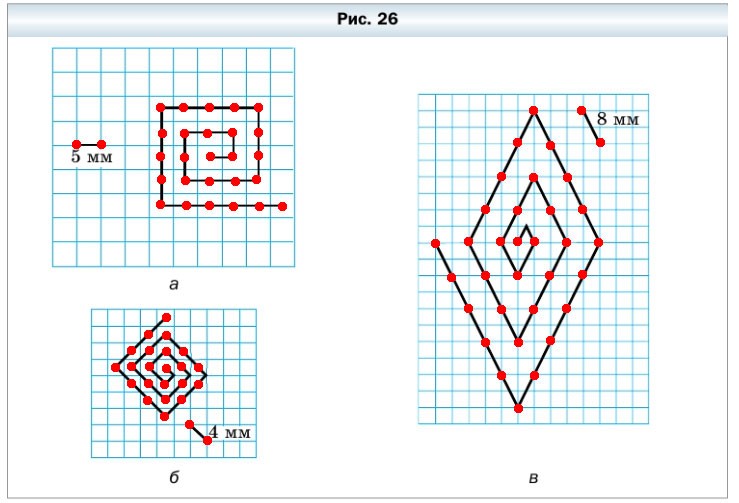
- а) ломаную можно разделить на 25 отрезков, равных заданному. Длина заданного отрезка 5 мм, значит длина ломаной: 5 • 25 = 125 мм.
- б) ломаную можно разделить на 21 отрезок, равных заданному. Длина заданного отрезка 4 мм, значит длина ломаной: 4 • 21 = 84 мм.
- в) ломаную можно разделить на 31 отрезок, равный заданному. Длина заданного отрезка 8 мм, значит длина ломаной 8 • 31 = 248 мм.
Ответ: 125 мм, 84 мм и 248 мм.
71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.
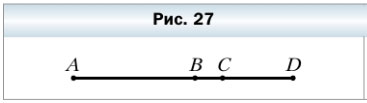
1) AB = AC — BC
8 — 2 = 6 (см) — длина отрезка AB.
2) AD = AB + BD
6 + 6 = 12 (см) — длина отрезка AD.
Ответ: AD = 12 см.
72. Известно, что MF= 30 см, ME = 18 см, KF = 22 см (рис. 28). Найдите длину отрезка КЕ.

1) EF = MF — ME
30 — 18 = 12 (см) — длина отрезка EF.
2) KE = KF — EF
22 — 12 = 10 (см) — длина отрезка KE.
Ответ: KE = 10 см.
73. Известно, что KP = PE = EF= FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.
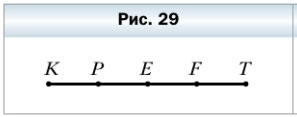
На рисунке 29 можно найти следующие равные отрезки:
KE = PF = ET = 4
KF = PT = 6
74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?
- Если на отрезке отметить семь точек на равном расстоянии, то получится 6 равных отрезков. Это значит, что на первом отрезке будет отмечено 6 отрезков по 3 см, а длина первого отрезка будет равна: 3 • 6 = 18 см.
- Если на отрезке отметить десять точек на равном расстоянии, то получится 9 равных отрезков. Это значит, что на втором отрезке будет отмечено 9 отрезков по 2 см, а длина второго отрезка будет равна: 2 • 6 = 18 см.
Это значит, что расстояние между крайними точками у первого и второго отрезка будет одинаковым.
Проверим вывод графически:

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = MС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

Для удобства обозначим равные отрезки отдельными цветами.
![]()
1) Известно, что МК = 4 см.
МК = MС + СК = 4 см
2) Известно, что ВМ = MС и KD = СК . Значит:
ВМ + KD = MС + СК = 4 см
3) ВD = ВМ + MС + KD + СК = (ВМ + KD) + (MС + СК) = 4 + 4 = 8 см
4) Мы знаем, что АЕ = 12 см, ВD = 8 см.
AQ + QB + DR + RE = АЕ — ВD = 12 — 8 = 4 см
5) Известно, что AQ = QB и DR = RE. Значит:
AQ + RE = QB + DR = 4 : 2 = 2 см
6) QR = АЕ — (AQ + RE) = 12 — 2 = 10 см
Ответ: QR = 10 см.
76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них были две отмеченные точки, не считая концов отрезков?

а) Надо отметить 4 точки: две на отрезке AB (например E и F) и две на отрезке CD (например H и G).
б) Надо отметить 3 точки: точку пересечения отрезков CD и AB (точка O) и по одной точке на отрезке CD (на?

