Каким свойством обладает действие умножения дробей
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
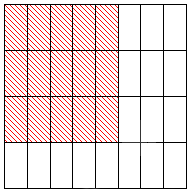
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: 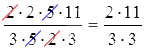 .
.
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7
Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
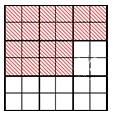
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Óìíîæåíèå îáûêíîâåííîé äðîáè íà äðîáü.
×òîáû ïåðåìíîæèòü îáûêíîâåííûå äðîáè, íåîáõîäèìî óìíîæèòü ÷èñëèòåëü íà ÷èñëèòåëü (ïîëó÷èì ÷èñëèòåëü ïðîèçâåäåíèÿ) è çíàìåíàòåëü íà çíàìåíàòåëü (ïîëó÷èì çíàìåíàòåëü ïðîèçâåäåíèÿ).
Ôîðìóëà óìíîæåíèÿ äðîáåé:
Íàïðèìåð:
Ïåðåä òåì, êàê ïðèñòóïèòü ê óìíîæåíèþ ÷èñëèòåëåé è çíàìåíàòåëåé, íåîáõîäèìî ïðîâåðèòü íà âîçìîæíîñòü ñîêðàùåíèÿ äðîáè. Åñëè ïîëó÷èòñÿ ñîêðàòèòü äðîáü, òî âàì ëåã÷å áóäåò äàëüøå ïðîèçâîäèòü ðàñ÷åòû.
Îáðàòèòå âíèìàíèå! Çäåñü íå íóæíî èñêàòü îáùèé çíàìåíàòåëü!!
Äåëåíèå îáûêíîâåííîé äðîáè íà äðîáü.
Äåëåíèå îáûêíîâåííîé äðîáè íà äðîáü ïðîèñõîäèò òàê: ïåðåâîðà÷èâàåòå âòîðóþ äðîáü (ò.å. ìåíÿåòå ÷èñëèòåëü è çíàìåíàòåëü ìåñòàìè) è ïîñëå ýòîãî äðîáè ïåðåìíîæàþòñÿ.
Ôîðìóëà äåëåíèÿ îáûêíîâåííûõ äðîáåé:
Íàïðèìåð:
Óìíîæåíèå äðîáè íà íàòóðàëüíîå ÷èñëî.
Îáðàòèòå âíèìàíèå! Ïðè óìíîæåíèè äðîáè íà íàòóðàëüíîå ÷èñëî, ÷èñëèòåëü äðîáè óìíîæàåòñÿ íà íàøå íàòóðàëüíîå ÷èñëî, à çíàìåíàòåëü äðîáè îñòàâëÿåì ïðåæíèì. Åñëè ðåçóëüòàòîì ïðîèçâåäåíèÿ îêàçàëàñü íåïðàâèëüíàÿ äðîáü, òî îáÿçàòåëüíî âûäåëèòå öåëóþ ÷àñòü, ïðåâðàòèâ íåïðàâèëüíóþ äðîáü â ñìåøàííóþ.

Äåëåíèå äðîáåé ñ ó÷àñòèåì íàòóðàëüíîãî ÷èñëà.
Ýòî íå òàê ñòðàøíî, êàê êàæåòñÿ. Êàê è â ñëó÷àå ñî ñëîæåíèåì, ïåðåâîäèì öåëîå ÷èñëî â äðîáü ñ åäèíèöåé â çíàìåíàòåëå. Íàïðèìåð:
Óìíîæåíèå ñìåøàííûõ äðîáåé.
Ïðàâèëà óìíîæåíèÿ äðîáåé (ñìåøàííûõ):
- ïðåîáðàçîâûâàåì ñìåøàííûå äðîáè â íåïðàâèëüíûå;
- ïåðåìíîæàåì ÷èñëèòåëè è çíàìåíàòåëè äðîáåé;
- ñîêðàùàåì äðîáü;
- åñëè ïîëó÷èëè íåïðàâèëüíóþ äðîáü, òî ïðåîáðàçîâûâàåì íåïðàâèëüíóþ äðîáü â ñìåøàííóþ.
Êàëüêóëÿòîð äðîáåé îíëàéí. Ñëîæåíèå, âû÷èòàíèå, óìíîæåíèå, äåëåíèå äðîáåé.
Êàëüêóëÿòîð äåñÿòè÷íûõ äðîáåé îíëàéí. Ïåðåâîä äåñÿòè÷íûõ äðîáåé â îáû÷íûå è îáû÷íûõ â äåñÿòè÷íûå.
Îáðàòèòå âíèìàíèå! ×òîáû óìíîæèòü ñìåøàííóþ äðîáü íà äðóãóþ ñìåøàííóþ äðîáü, íóæíî, äëÿ íà÷àëà, ïðèâåñòè èõ ê âèäó íåïðàâèëüíûõ äðîáåé, à äàëåå óìíîæèòü ïî ïðàâèëó óìíîæåíèÿ îáûêíîâåííûõ äðîáåé.

Âòîðîé ñïîñîá óìíîæåíèÿ äðîáè íà íàòóðàëüíîå ÷èñëî.
Áûâàåò áîëåå óäîáíî èñïîëüçîâàòü âòîðîé ñïîñîá óìíîæåíèÿ îáûêíîâåííîé äðîáè íà ÷èñëî.
Îáðàòèòå âíèìàíèå! Äëÿ óìíîæåíèÿ äðîáè íà íàòóðàëüíîå ÷èñëî íåîáõîäèìî çíàìåíàòåëü äðîáè ðàçäåëèòü íà ýòî ÷èñëî, à ÷èñëèòåëü îñòàâèòü áåç èçìåíåíèÿ.

Èç, ïðèâåäåííîãî âûøå, ïðèìåðà ïîíÿòíî, ÷òî ýòîò âàðèàíò óäîáíåé äëÿ èñïîëüçîâàíèÿ, êîãäà çíàìåíàòåëü äðîáè äåëèòñÿ áåç îñòàòêà íà íàòóðàëüíîå ÷èñëî.
Ìíîãîýòàæíûå äðîáè.
 ñòàðøèõ êëàññàõ çà÷àñòóþ âñòðå÷àþòñÿ òðåõýòàæíûå (èëè áîëüøå) äðîáè. Ïðèìåð:
×òîáû ïðèâåñòè òàêóþ äðîáü ê ïðèâû÷íîìó âèäó, èñïîëüçóþò äåëåíèå ÷åðåç 2 òî÷êè:
Îáðàòèòå âíèìàíèå!  äåëåíèè äðîáåé î÷åíü âàæåí ïîðÿäîê äåëåíèÿ. Áóäüòå âíèìàòåëüíû, çäåñü ëåãêî çàïóòàòüñÿ.
Îáðàòèòå âíèìàíèå, íàïðèìåð:
Ïðè äåëåíèè åäèíèöû íà ëþáóþ äðîáü, ðåçóëüòàòîì áóäåò òàæå ñàìàÿ äðîáü, òîëüêî ïåðåâåðíóòàÿ:
Ïðàêòè÷åñêèå ñîâåòû ïðè óìíîæåíèè è äåëåíèè äðîáåé:
1. Ñàìûì âàæíûì â ðàáîòå ñ äðîáíûìè âûðàæåíèÿìè ÿâëÿåòñÿ àêêóðàòíîñòü è âíèìàòåëüíîñòü. Âñå âû÷èñëåíèÿ äåëàéòå âíèìàòåëüíî è àêêóðàòíî, ñîñðåäîòî÷åííî è ÷¸òêî. Ëó÷øå çàïèøèòå íåñêîëüêî ëèøíèõ ñòðî÷åê â ÷åðíîâèêå, ÷åì çàïóòàòüñÿ â ðàñ÷åòàõ â óìå.
2. Â çàäàíèÿõ ñ ðàçíûìè âèäàìè äðîáåé — ïåðåõîäèòå ê âèäó îáûêíîâåííûõ äðîáåé.
3. Âñå äðîáè ñîêðàùàåì äî òåõ ïîð, ïîêà ñîêðàùàòü óæå áóäåò íåâîçìîæíî.
4. Ìíîãîýòàæíûå äðîáíûå âûðàæåíèÿ ïðèâîäèì â âèä îáûêíîâåííûõ, ïîëüçóÿñü äåëåíèåì ÷åðåç 2 òî÷êè.
5. Åäèíèöó íà äðîáü äåëèì â óìå, ïðîñòî ïåðåâîðà÷èâàÿ äðîáü.
Êàëüêóëÿòîð äðîáåé | |
| Êàëüêóëÿòîð äðîáåé — ñëîæåíèå, âû÷èòàíèå, óìíîæåíèå, äåëåíèå äðîáåé â òîì ÷èñëå ñ öåëûìè ÷èñëàìè. | |
| Êàëüêóëÿòîð äðîáåé | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Îáûêíîâåííûå äðîáè | |
| Ïðàâèëüíûå, íåïðàâèëüíûå, ñìåøàííûå, ñîñòàâíûå, äåñÿòè÷íûå äðîáè, ñîêðàùåíèå, äåëåíèå äðîáåé | |
| Îáûêíîâåííûå äðîáè | |
Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Äðîáè. Ñðàâíåíèå äðîáåé. | |
| Ïðàâèëà ñðàâíåíèÿ îáûêíîâåííûõ äðîáåé çàâèñÿò îò âèäà äðîáè (ïðàâèëüíàÿ, íåïðàâèëüíàÿ, ñìåøàííàÿ äðîáü) è îò çíàìåíàòåëåé (îäèíàêîâûå èëè ðàçíûå) ó ñðàâíèâàåìûõ äðîáåé. | |
| Äðîáè. Ñðàâíåíèå äðîáåé. | |
