Каким свойством должны обладать кролики фибоначчи

Ëþäè ïîâñþäó èñïîëüçóþò ìàòåìàòèêó, è äàæå ñàìà ïðèðîäà èùåò ìàòåìàòè÷åñêèå çàêîíû. Ýòî ïîñò î êðàñèâîé êîíñòàíòå, íàéäåííîé è ÷åëîâåêîì, è ýâîëþöèåé
 12 âåêå ðîäèëñÿ Ëåîíàðäî Ïèçàíñêèé. Îí ñòàë ïåðâûì êðóïíûì åâðîïåéñêèì ìàòåìàòèêîì. Èìåííî îí ïîëîæèë íà÷àëî èñïîëüçîâàíèþ ïîçèöèîííîé ñèñòåìû ñ÷èñëåíèÿ. Ïðîùå ãîâîðÿ, áëàãîäàðÿ åìó ìû ïèøåì ÷èñëà óäîáíûìè àðàáñêèìè öèôðàìè, à íå äëèííûìè ðÿäàìè ðèìñêèõ. Ñðàâíèòå: MMXVIII è 2018
Âàì ýòîò ìàòåìàòèê ìîæåò áûòü èçâåñòåí ïîä èìåíåì Ôèáîíà÷÷è. Îäíàæäû, îí ïîñòàâèë ñëåäóþùóþ çàäà÷ó:
Ïîïûòàåìñÿ ðåøèòü å¸! Òàê âûãëÿäÿò íàøè êðîëèêè â ïåðâûé ìåñÿö ìàëåíüêèå ìàëü÷èê è äåâî÷êà
 òðåòèé ðîæäàåòñÿ åù¸ îäíà ïàðà òàêæå ìàëü÷èê è äåâî÷êà. Èç-çà òîãî, ÷òî òóò ïðîèñõîäèò, íàçîâ¸ì ýòî ñåìåéñòâî Òàðãàðèåíàìè

 ÷åòâ¸ðòûé ìåñÿö íàøè ïåðâîíà÷àëüíûå êðîëèêè ðîæäàþò åù¸ îäíó ïàðó, à ìàëûøè Äåéåíåðèñ è Âèçåðèñ ïîäðàñòàþò

Èòàê, ñêîëüêî æå ïàð êðîëèêîâ áóäåò ÷åðåç 12 ìåñÿöåâ? Äîïóñòèì, ÷òî êðîëèêè æèâóò â èäåàëüíûõ óñëîâèÿõ íå ñòàðåþò, íå ïîãèáàþò è íå ñâåðãàþòñÿ äðóãîé äèíàñòèåé
Âçðîñëûõ êðîëèêîâ áóäåò ñòîëüêî æå, ñêîëüêî âñåãî êðîëèêîâ áûëî íà ïðåäûäóùåì øàãå: òàê êàê âçðîñëûå îñòàíóòñÿ, à ìàëûøè ïîäðàñòóò. Çàïèøåì ýòî:
âçðîñëûå[n] = êðîëèêè[n-1]
Äåòåé æå â íîâîì ìåñÿöó áóäåò ñòîëüêî æå, ñêîëüêî áûëî âçðîñëûõ â ïðîøëîì. À èõ, êàê ãîâîðèò ôîðìóëà âûøå, ñòîëüêî æå, ñêîëüêî êðîëèêîâ âñåãî â ïîçàïðîøëîì!
äåòè[n] = âçðîñëûå[n-1] = êðîëèêè[n-2]
Ïîëó÷àåì èòîãîâóþ ôîðìóëó: êðîëèêîâ â ýòîì ìåñÿöå áóäåò ñòîëüêî, ñêîëüêî èõ áûëî âìåñòå â ïðåäûäóùèå 2 ìåñÿöà:
êðîëèêè[n] = êðîëèêè[n-1] + êðîëèêè[n-2]
Òî åñòü, íàøó ïîñëåäîâàòåëüíîñòü ìîæíî ïðîäëèòü íà ñêîëüêî óãîäíî ìåñÿöåâ âïåð¸ä! Ïîëó÷èì 1 1 2 3 5 8 13 21 Ýòî íàçûâàåòñÿ ïîñëåäîâàòåëüíîñòüþ Ôèáîíà÷÷è. Ñìîæåòå ëè âû òåïåðü äàòü îòâåò íà çàäà÷ó?
Êðàñîòà ïîñëåäîâàòåëüíîñòè
Îêàçàëîñü, ÷òî ýòîò ðÿä ÷èñåë, íàéäåííûé ïðè ïîìîùè òàêîé àáñòðàêòíîé çàäà÷è, îáëàäàåò î÷åíü èíòåðåñíûìè ñâîéñòâàìè! Íåñìîòðÿ íà òî, ÷òî êðîëèêè â ðåàëüíîé æèçíè âåäóò ñåáÿ íå òàê, ýòà ïîñëåäîâàòåëüíîñòü ïðèñóòñòâóåò â ïðèðîäå ïîâñþäó
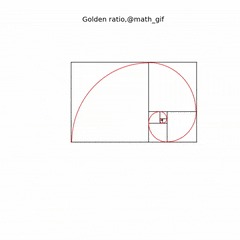
Ñòîðîíû ïðÿìîóãîëüíèêà ýòî ÷èñëà Ôèáîíà÷÷è
Âîò îäíî èç å¸ ñâîéñòâ. Îòíîøåíèå ñîñåäíèõ ÷èñåë â íåé íàçâàëè çîëîòûì ñîîòíîøåíèåì. Ñîñåäíèå ÷èñëà îòíîñÿòñÿ äðóã ê äðóãó îäèíàêîâî (÷åì äàëüøå, òåì òî÷íåå ýòî ïðèáëèæàåòñÿ ê îäíîìó ÷èñëó, ðàâíîìó 1,618).
Ñ÷èòàåòñÿ, ÷òî «çîëîòûå ïðîïîðöèè» ëó÷øå è ïðèÿòíåå âîñïðèíèìàþòñÿ ÷åëîâåêîì. Ïàðôåíîí ñòðîèëñÿ ñ ìíîæåñòâîì àðõèòåêòóðíûõ óõèùðåíèé òàê, ÷òîáû âûãëÿäåòü íàèáîëåå ïðèÿòíî. Îäíèì èç òàêèõ ïðè¸ìîâ ñ÷èòàåòñÿ çîëîòîå ñå÷åíèå:

Íî ñàìûå ïðåêðàñíûå ïðèìåðû çîëîòîãî ñîîòíîøåíèÿ ìîæíî íàéòè â ïðèðîäå. Íàïðèìåð, ðàêîâèíû ìîëëþêîâ:

Òàêàÿ ôîðìà íàèáîëåå âûãîäíà è âûðàáîòàëàñü ýâîëþöèîííî. Ðàçáåð¸ì, ïî÷åìó ýòî òàê è åù¸ îäíî ñâîéñòâî çîëîòîãî îòíîøåíèÿ íà ìî¸ì ëþáèìîì ïðèìåðå
Ðàñòåíèÿ
Ïðåäñòàâüòå ñåáÿ ðàñòåíèåì. Íàäåþñü, âàì â ãîëîâó ïðèø¸ë ìîãó÷èé äóá, íî äëÿ ýòîãî ïðèìåðà ëó÷øå ïðåäñòàâèòü öâåòîê èëè, ñêàæåì, ñïèðàëüíûé àëîý

Ïðåäïîëîæèì, âàì òîëüêî ïðåäñòîèò âûðàñòèòü ëèñòüÿ. Áóäó÷è î÷åíü óìíûì àëîý, âû õîòèòå ðàñïîëîæèòü èõ ìàêñèìàëüíî ýôôåêòèâíî. Åäèíñòâåííûé ïàðàìåòð, êîòîðûé âàì äîñòóïåí ýòî óãîë, íà êîòîðûé ìîæíî ïîâåðíóòü ñëåäóþùèé ëèñò
Ðàçáåð¸ì íà ïðèìåðå. Ïåðâûé ëèñò ìîæíî ðàñïîëîæèòü, ãäå óãîäíî

Ïðåäïîëîæèì, âûáðàí óãîë ïîâîðîòà 180 ãðàäóñîâ. Èëè, áîëåå ïðîñòî ïîëîâèíà îêðóæíîñòè, ½. Òîãäà âòîðîé ëèñò áóäåò íàïðîòèâ. Òðåòèé íà ìåñòå ïåðâîãî è òàê äàëåå



Åñëè âû õîòèòå áûòü êîíêóðåíòîñïîñîáíûì ðàñòåíèåì, à íå îáíèìàøåê, òî êàæåòñÿ, ýòî íå ñàìûé ýôôåêòèâíûé ñïîñîá. Ìîæåò áûòü ïîïðîáîâàòü 1/3 îêðóæíîñòè?

Òîãäà áóäåò 3 «ïèêà» è âîçìîæíîñòü âäîõíîâèòü áðàòüåâ Ðàéò.
Íî ïîõîæå, ÷òî ÷èñëî ïèêîâ ðàâíî çíàìåíàòåëþ äðîáè! Ðàñòåíèå, çíàêîìîå ñ ìàòåìàòèêîé, ìîãëî áû ñêàçàòü, ÷òî òîãäà âûãîäíåå âñåãî èñïîëüçîâàòü èððàöèîíàëüíîå ÷èñëî êîòîðîå íåëüçÿ ïðåäñòàâèòü â âèäå äðîáè. Òàêèì ÷èñëîì è ÿâëÿåòñÿ çîëîòîå ñîîòíîøåíèå φ! À ñàìûì âûãîäíûì îêàçûâàåòñÿ óãîë ïîâîðîòà 1/φ. Òàê áóäåò âûãëÿäåòü ðàñïðåäåëåíèå ëèñòîâ, èñïîëüçóþùåå çîëîòîå ñîîòíîøåíèå:
À òàê âûãëÿäèò ðåàëüíîå ðàñòåíèå!

Ìîæíî ïîèãðàòü ñ ñèìóëÿöèåé ñàìîñòîÿòåëüíî
Åñëè íðàâÿòñÿ ïîñòû î íàóêå è ó÷¸áå, çàãëÿäûâàéòå êî ìíå â ÂÊ è òåëåãðàì
Числа Фибоначчи названы в честь Леонардо Фибоначчи из города Пизы (современная Италия). На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.
Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.
Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например, 144/89 вы в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.
Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.
Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.
Числа Фибоначчи в природе
Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.
Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность.
Ветви дерева демонстрируют последовательность Фибоначчи.
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.
Числа Фибоначчи в теле человека
Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.
Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.
Числа Фибоначчи в биржевой торговле
Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.
Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2%(соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.
Числа Фибоначчи в фотографии и искусстве
В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.
Сетка фи (красные линии) и спираль Фиббоначи в кадре.
Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.
Может именно из-за этого Дональд Трамп был избран президентом? (шутка):
Тем не менее, никогда не стоит недооценивать скрытые силы последовательности Фибоначчи.
Ëþäè ïîâñþäó èñïîëüçóþò ìàòåìàòèêó, è äàæå ñàìà ïðèðîäà èùåò ìàòåìàòè÷åñêèå çàêîíû. Ýòî ïîñò î êðàñèâîé êîíñòàíòå, íàéäåííîé è ÷åëîâåêîì, è ýâîëþöèåé
 12 âåêå ðîäèëñÿ Ëåîíàðäî Ïèçàíñêèé. Îí ñòàë ïåðâûì êðóïíûì åâðîïåéñêèì ìàòåìàòèêîì. Èìåííî îí ïîëîæèë íà÷àëî èñïîëüçîâàíèþ ïîçèöèîííîé ñèñòåìû ñ÷èñëåíèÿ. Ïðîùå ãîâîðÿ, áëàãîäàðÿ åìó ìû ïèøåì ÷èñëà óäîáíûìè àðàáñêèìè öèôðàìè, à íå äëèííûìè ðÿäàìè ðèìñêèõ. Ñðàâíèòå: MMXVIII è 2018
Âàì ýòîò ìàòåìàòèê ìîæåò áûòü èçâåñòåí ïîä èìåíåì Ôèáîíà÷÷è. Îäíàæäû, îí ïîñòàâèë ñëåäóþùóþ çàäà÷ó:
Ïîïûòàåìñÿ ðåøèòü å¸! Òàê âûãëÿäÿò íàøè êðîëèêè â ïåðâûé ìåñÿö ìàëåíüêèå ìàëü÷èê è äåâî÷êà
 òðåòèé ðîæäàåòñÿ åù¸ îäíà ïàðà òàêæå ìàëü÷èê è äåâî÷êà. Èç-çà òîãî, ÷òî òóò ïðîèñõîäèò, íàçîâ¸ì ýòî ñåìåéñòâî Òàðãàðèåíàìè

 ÷åòâ¸ðòûé ìåñÿö íàøè ïåðâîíà÷àëüíûå êðîëèêè ðîæäàþò åù¸ îäíó ïàðó, à ìàëûøè Äåéåíåðèñ è Âèçåðèñ ïîäðàñòàþò

Èòàê, ñêîëüêî æå ïàð êðîëèêîâ áóäåò ÷åðåç 12 ìåñÿöåâ? Äîïóñòèì, ÷òî êðîëèêè æèâóò â èäåàëüíûõ óñëîâèÿõ íå ñòàðåþò, íå ïîãèáàþò è íå ñâåðãàþòñÿ äðóãîé äèíàñòèåé
Âçðîñëûõ êðîëèêîâ áóäåò ñòîëüêî æå, ñêîëüêî âñåãî êðîëèêîâ áûëî íà ïðåäûäóùåì øàãå: òàê êàê âçðîñëûå îñòàíóòñÿ, à ìàëûøè ïîäðàñòóò. Çàïèøåì ýòî:
âçðîñëûå[n] = êðîëèêè[n-1]
Äåòåé æå â íîâîì ìåñÿöó áóäåò ñòîëüêî æå, ñêîëüêî áûëî âçðîñëûõ â ïðîøëîì. À èõ, êàê ãîâîðèò ôîðìóëà âûøå, ñòîëüêî æå, ñêîëüêî êðîëèêîâ âñåãî â ïîçàïðîøëîì!
äåòè[n] = âçðîñëûå[n-1] = êðîëèêè[n-2]
Ïîëó÷àåì èòîãîâóþ ôîðìóëó: êðîëèêîâ â ýòîì ìåñÿöå áóäåò ñòîëüêî, ñêîëüêî èõ áûëî âìåñòå â ïðåäûäóùèå 2 ìåñÿöà:
êðîëèêè[n] = êðîëèêè[n-1] + êðîëèêè[n-2]
Òî åñòü, íàøó ïîñëåäîâàòåëüíîñòü ìîæíî ïðîäëèòü íà ñêîëüêî óãîäíî ìåñÿöåâ âïåð¸ä! Ïîëó÷èì 1 1 2 3 5 8 13 21 Ýòî íàçûâàåòñÿ ïîñëåäîâàòåëüíîñòüþ Ôèáîíà÷÷è. Ñìîæåòå ëè âû òåïåðü äàòü îòâåò íà çàäà÷ó?
Êðàñîòà ïîñëåäîâàòåëüíîñòè
Îêàçàëîñü, ÷òî ýòîò ðÿä ÷èñåë, íàéäåííûé ïðè ïîìîùè òàêîé àáñòðàêòíîé çàäà÷è, îáëàäàåò î÷åíü èíòåðåñíûìè ñâîéñòâàìè! Íåñìîòðÿ íà òî, ÷òî êðîëèêè â ðåàëüíîé æèçíè âåäóò ñåáÿ íå òàê, ýòà ïîñëåäîâàòåëüíîñòü ïðèñóòñòâóåò â ïðèðîäå ïîâñþäó

Ñòîðîíû ïðÿìîóãîëüíèêà ýòî ÷èñëà Ôèáîíà÷÷è
Âîò îäíî èç å¸ ñâîéñòâ. Îòíîøåíèå ñîñåäíèõ ÷èñåë â íåé íàçâàëè çîëîòûì ñîîòíîøåíèåì. Ñîñåäíèå ÷èñëà îòíîñÿòñÿ äðóã ê äðóãó îäèíàêîâî (÷åì äàëüøå, òåì òî÷íåå ýòî ïðèáëèæàåòñÿ ê îäíîìó ÷èñëó, ðàâíîìó 1,618).
Ñ÷èòàåòñÿ, ÷òî «çîëîòûå ïðîïîðöèè» ëó÷øå è ïðèÿòíåå âîñïðèíèìàþòñÿ ÷åëîâåêîì. Ïàðôåíîí ñòðîèëñÿ ñ ìíîæåñòâîì àðõèòåêòóðíûõ óõèùðåíèé òàê, ÷òîáû âûãëÿäåòü íàèáîëåå ïðèÿòíî. Îäíèì èç òàêèõ ïðè¸ìîâ ñ÷èòàåòñÿ çîëîòîå ñå÷åíèå:

Íî ñàìûå ïðåêðàñíûå ïðèìåðû çîëîòîãî ñîîòíîøåíèÿ ìîæíî íàéòè â ïðèðîäå. Íàïðèìåð, ðàêîâèíû ìîëëþêîâ:
Òàêàÿ ôîðìà íàèáîëåå âûãîäíà è âûðàáîòàëàñü ýâîëþöèîííî. Ðàçáåð¸ì, ïî÷åìó ýòî òàê è åù¸ îäíî ñâîéñòâî çîëîòîãî îòíîøåíèÿ íà ìî¸ì ëþáèìîì ïðèìåðå
Ðàñòåíèÿ
Ïðåäñòàâüòå ñåáÿ ðàñòåíèåì. Íàäåþñü, âàì â ãîëîâó ïðèø¸ë ìîãó÷èé äóá, íî äëÿ ýòîãî ïðèìåðà ëó÷øå ïðåäñòàâèòü öâåòîê èëè, ñêàæåì, ñïèðàëüíûé àëîý

Ïðåäïîëîæèì, âàì òîëüêî ïðåäñòîèò âûðàñòèòü ëèñòüÿ. Áóäó÷è î÷åíü óìíûì àëîý, âû õîòèòå ðàñïîëîæèòü èõ ìàêñèìàëüíî ýôôåêòèâíî. Åäèíñòâåííûé ïàðàìåòð, êîòîðûé âàì äîñòóïåí ýòî óãîë, íà êîòîðûé ìîæíî ïîâåðíóòü ñëåäóþùèé ëèñò
Ðàçáåð¸ì íà ïðèìåðå. Ïåðâûé ëèñò ìîæíî ðàñïîëîæèòü, ãäå óãîäíî

Ïðåäïîëîæèì, âûáðàí óãîë ïîâîðîòà 180 ãðàäóñîâ. Èëè, áîëåå ïðîñòî ïîëîâèíà îêðóæíîñòè, ½. Òîãäà âòîðîé ëèñò áóäåò íàïðîòèâ. Òðåòèé íà ìåñòå ïåðâîãî è òàê äàëåå



Åñëè âû õîòèòå áûòü êîíêóðåíòîñïîñîáíûì ðàñòåíèåì, à íå îáíèìàøåê, òî êàæåòñÿ, ýòî íå ñàìûé ýôôåêòèâíûé ñïîñîá. Ìîæåò áûòü ïîïðîáîâàòü 1/3 îêðóæíîñòè?

Òîãäà áóäåò 3 «ïèêà» è âîçìîæíîñòü âäîõíîâèòü áðàòüåâ Ðàéò.
Íî ïîõîæå, ÷òî ÷èñëî ïèêîâ ðàâíî çíàìåíàòåëþ äðîáè! Ðàñòåíèå, çíàêîìîå ñ ìàòåìàòèêîé, ìîãëî áû ñêàçàòü, ÷òî òîãäà âûãîäíåå âñåãî èñïîëüçîâàòü èððàöèîíàëüíîå ÷èñëî êîòîðîå íåëüçÿ ïðåäñòàâèòü â âèäå äðîáè. Òàêèì ÷èñëîì è ÿâëÿåòñÿ çîëîòîå ñîîòíîøåíèå φ! À ñàìûì âûãîäíûì îêàçûâàåòñÿ óãîë ïîâîðîòà 1/φ. Òàê áóäåò âûãëÿäåòü ðàñïðåäåëåíèå ëèñòîâ, èñïîëüçóþùåå çîëîòîå ñîîòíîøåíèå:

À òàê âûãëÿäèò ðåàëüíîå ðàñòåíèå!

Ìîæíî ïîèãðàòü ñ ñèìóëÿöèåé ñàìîñòîÿòåëüíî
Åñëè íðàâÿòñÿ ïîñòû î íàóêå è ó÷¸áå, çàãëÿäûâàéòå êî ìíå â ÂÊ è òåëåãðàì
ЧиÑла ФибонаÑÑи Ð·Ð½Ð°ÐºÐ¾Ð¼Ñ Ð¼Ð½Ð¾Ð³Ð¸Ð¼ маÑемаÑикам. РаÑÑмоÑÑим в данной замеÑке ÑÑаÑиннÑй ÑпоÑоб полÑÑÐµÐ½Ð¸Ñ ÑказаннÑÑ ÑиÑел и одно оÑигиналÑное пÑименение ÑÑÐ¸Ñ ÑиÑел Ð´Ð»Ñ Ð¿ÑимеÑного пеÑевода Ð¼Ð¸Ð»Ñ Ð² киломеÑÑÑ.
ÐÑолики ФибонаÑÑи
ÐаннаÑ задаÑа пÑидÑмана иÑалÑÑнÑким ÑÑенÑм ФибонаÑÑи в 13-м веке.
ÐекÑо пÑиобÑел паÑÑ ÐºÑоликов и помеÑÑил иÑ
в огоÑоженнÑй Ñо вÑеÑ
ÑÑоÑон загон. СколÑко кÑоликов бÑÐ´ÐµÑ ÑеÑез год, еÑли ÑÑиÑаÑÑ, ÑÑо каждÑй меÑÑÑ Ð¿Ð°Ñа Ð´Ð°ÐµÑ Ð² каÑеÑÑве пÑиплода новÑÑ Ð¿Ð°ÑÑ ÐºÑоликов, коÑоÑÑе Ñо вÑоÑого меÑÑÑа жизни Ñакже наÑинаÑÑ Ð¿ÑиноÑиÑÑ Ð¿Ñиплод?

ÐÑвеÑ: 377 паÑ. РпеÑвÑй меÑÑÑ ÐºÑоликов окажеÑÑÑ Ñже 2 паÑÑ: 1 пеÑвонаÑалÑÐ½Ð°Ñ Ð¿Ð°Ñа, давÑÐ°Ñ Ð¿Ñиплод, и 1 ÑодивÑаÑÑÑ Ð¿Ð°Ñа. Ðо вÑоÑой меÑÑÑ ÐºÑоликов бÑÐ´ÐµÑ 3 паÑÑ: 1 пеÑвонаÑалÑнаÑ, Ñнова давÑÐ°Ñ Ð¿Ñиплод, 1 ÑаÑÑÑÑÐ°Ñ Ð¸ 1 ÑодивÑаÑÑÑ. Ð ÑÑеÑÑем меÑÑÑе – 5 паÑ: 2 паÑÑ, давÑие пÑиплод, 1 ÑаÑÑÑÑÐ°Ñ Ð¸ 2 ÑодивÑиеÑÑ. Ð ÑеÑвеÑÑом меÑÑÑе – 8 паÑ: 3 паÑÑ, давÑие пÑиплод, 2 ÑаÑÑÑÑие паÑÑ, 3 ÑодивÑиеÑÑ Ð¿Ð°ÑÑ. ÐÑÐ¾Ð´Ð¾Ð»Ð¶Ð°Ñ ÑаÑÑмоÑÑение по меÑÑÑам, можно ÑÑÑановиÑÑ ÑвÑÐ·Ñ Ð¼ÐµÐ¶Ð´Ñ ÐºÐ¾Ð»Ð¸ÑеÑÑвами кÑоликов в ÑекÑÑий меÑÑÑ Ð¸ в два пÑедÑдÑÑÐ¸Ñ . ÐÑли обознаÑиÑÑ ÐºÐ¾Ð»Ð¸ÑеÑÑво Ð¿Ð°Ñ ÑеÑез N, а ÑеÑез m – поÑÑдковÑй Ð½Ð¾Ð¼ÐµÑ Ð¼ÐµÑÑÑа, Ñо Nm = Nm-1 + Nm-2 . С помоÑÑÑ ÑÑого вÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ ÑаÑÑÑиÑÑваÑÑ ÐºÐ¾Ð»Ð¸ÑеÑÑво кÑоликов по меÑÑÑам года: 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
ÐамеÑание. ÐонеÑно же кÑо-Ñо ÑкажеÑ, ÑÑо кÑолики ÑмиÑаÑÑ, ÑÑо не обÑзаÑелÑно в новой паÑе бÑдÑÑ ÑÐ°Ð¼ÐµÑ Ð¸ Ñамка. Ðадо понимаÑÑ, ÑÑо ÑÑо Ð½ÐµÐºÐ°Ñ Ð¼Ð°ÑемаÑиÑеÑÐºÐ°Ñ Ð¼Ð¾Ð´ÐµÐ»Ñ, коÑоÑÐ°Ñ Ð¿ÑÐµÐ´Ð¿Ð¾Ð»Ð°Ð³Ð°ÐµÑ Ð½ÐµÐºÐ¾ÑоÑÑе допÑÑениÑ. ÐÐ¾Ñ Ð¼Ñ Ð¸ вводим допÑÑениÑ, ÑÑо кÑолики не ÑмиÑаÑÑ, в паÑе ÑÐ°Ð¼ÐµÑ Ð¸ Ñамка.
ÐеÑевод Ð¼Ð¸Ð»Ñ Ð² киломеÑÑÑ
ÐамеÑена инÑеÑеÑÐ½Ð°Ñ Ð¾ÑобенноÑÑÑ ÑиÑел ФибонаÑÑи Ð´Ð»Ñ Ð¿ÑимеÑного пеÑевода киломеÑÑов в мили.ÐапÑимеÑ, 8 Ð¼Ð¸Ð»Ñ ÑÑо пÑимеÑно 13 киломеÑÑов. ÐбÑаÑиÑе внимание на ÑиÑÑÑ 8 в поÑледоваÑелÑноÑÑи ФибонаÑÑи, где поÑле ÑиÑÑÑ Â«Ð²Ð¾ÑемÑ» Ð¸Ð´ÐµÑ ÑиÑÑа «ÑÑинадÑаÑÑ». Ðли Ð²Ð¾Ñ ÐµÑе пÑимеÑ. ÐопÑÑÑим Ð¼Ñ Ñ Ð¾Ñим пеÑевеÑÑи в киломеÑÑÑ Ð·Ð½Ð°Ñение «13 милÑ». ÐоÑмоÑÑиÑе на ÑиÑловÑÑ Ð¿Ð¾ÑледоваÑелÑноÑÑÑ, и Ð²Ñ ÑвидиÑе, ÑÑо в ней поÑле ÑиÑÑÑ Â«13» Ð¸Ð´ÐµÑ ÑиÑÑа «21». ÐÑо ознаÑаеÑ, ÑÑо 13 Ð¼Ð¸Ð»Ñ = 21 киломеÑÑ. РиÑоге пÑименив ÑиÑла ФибонаÑÑи в каÑеÑÑве пÑеобÑÐ°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¼Ð¸Ð»ÐµÐ¹ в киломеÑÑÑ, Ð¼Ñ Ð¼Ð¾Ð¶ÐµÐ¼ без ÑакÑиÑеÑÐºÐ¸Ñ Ð²ÑÑиÑлений макÑималÑно бÑÑÑÑо пеÑевеÑÑи мили в киломеÑÑÑ
РнаÑÑоÑÑее вÑÐµÐ¼Ñ ÑабоÑе в ÐнÑеÑÐ½ÐµÑ Ð¾ÑводиÑÑÑ Ð±Ð¾Ð»ÑÑое внимание. ÐÑобое меÑÑо занимаÑÑ Ð¿Ñодажи, Ñ.к. лÑди заинÑеÑеÑÐ¾Ð²Ð°Ð½Ñ Ð² покÑÐ¿ÐºÐ°Ñ ÑеÑез ÐнÑеÑнеÑ, Ð¼Ñ Ð¶Ðµ Ñ Ð¾Ñим наÑÑиÑÑ Ð²Ð°Ñ Ð¿ÑодаваÑÑ. ÐÐ»Ñ ÑÑого Ð¼Ñ Ð½Ð°ÑÑим ваÑ оÑÑÑеÑÑвлÑÑÑ Ð¾ÑÐµÐ½ÐºÑ ÑÑÑекÑивноÑÑи ваÑего ÑайÑа, пÑодвигаÑÑ ÑÐ°Ð¹Ñ Ð² ÑоÑиалÑнÑÑ ÑеÑÑÑ , ÑазÑабоÑаÑÑ ÐºÐ¾Ð½ÑепÑÐ¸Ñ Ð¸ план ÑобÑÑвенной маÑкеÑинговой кампании и Ð¼Ð½Ð¾Ð³Ð¾Ð¼Ñ Ð´ÑÑгомÑ. РекомендÑем запиÑаÑÑÑÑ Ð½Ð°Â Ð¸Ð½ÑеÑÐ½ÐµÑ Ð¼Ð°ÑкеÑинг обÑÑение.
