Какие углы называются вертикальными свойство смежных углов

Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ.
Êàêèå óãëû íàçûâàþòñÿ ñìåæíûìè?
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ. Äëÿ óãëà 135 ãðàäóñîâ ñìåæíûì áóäåò óãîë ðàâíûé 45 ãðàäóñàì. Äëÿ óãëà x ãðàäóñîâ ñìåæíûì ÿâëÿåòñÿ óãîë (180 – x) ãðàäóñîâ. |  |
Äâà ñìåæíûõ óãëà — ýòî óãëû, ñ îäíîé îáùåé ñòîðîíîé, à îñòàëüíûå ñòîðîíû íàõîäÿòñÿ íà îäíîé ïðÿìîé.
Ïðè ïåðåñå÷åíèè 2-õ ïðÿìûõ ïîëó÷àåòñÿ 4-ðå ïàðû ñìåæíûõ óãëîâ:
∠1 è ∠2, ∠3 è ∠4, ∠1 è ∠3, ∠2 è ∠4 Íî, òàê êàê ∠1 =∠4, ∠2 = ∠3 (êàê âåðòèêàëüíûå), òî äîñòàòî÷íî ðàññìàòðèâàòü òîëüêî îäíó èç ýòèõ ïàð. |  |
Ñâîéñòâî ñìåæíûõ óãëîâ.
×åìó ðàâíà ñóììà ñìåæíûõ óãëîâ?
Ñìåæíûå óãëû ðàâíû: ñóììà ñìåæíûõ óãëîâ 180º.
1. α+ β= 180°
2. α= 180°−β
Ñëåäñòâèÿ èç òåîðåìû î ñìåæíûõ óãëàõ.
- Åñëè 2 óãëà ðàâíû, òî ñìåæíûå èì óãëû òîæå ðàâíû.
- Åñëè óãîë íå ðàçâåðíóòûé, çíà÷èò îí ≠180°.
- Ñìåæíûé óãîë äëÿ ïðÿìîãî óãëà (ò.å. óãëà, ó íåãî ãðàäóñíàÿ ìåðà = 90°), òîæå ïðÿìîé.
- Ñìåæíûé óãîë äëÿ îñòðîãî óãëà (ãðàäóñíàÿ ìåðà ìåíüøå 90°), áóäåò òóïûì (ãðàäóñíàÿ ìåðà áîëüøå
90°), à ñìåæíûé òóïîìó — îñòðûì.
Òðèãîíîìåòðè÷åñêèå ñîîòíîøåíèÿ.
- Ñèíóñû ñìåæíûõ óãëîâ îäèíàêîâû. Èõ êîñèíóñû è òàíãåíñû ðàâíû ïî âåëè÷èíå, íî èìåþò
ïðîòèâîïîëîæíûå çíàêè (èñêëþ÷åíèå íåîïðåäåëåííûå çíà÷åíèÿ).
- ×òîáû ïîñòðîèòü óãîë, ñìåæíûé ñóùåñòâóþùåìó, íåîáõîäèìî îäíó èç ñòîðîí íàøåãî óãëà ïðîäëèòü
äàëüøå âåðøèíû.

Ðàññìîòðèì ïðèìåð:
Çàäàíèå. ×åìó áóäåò ðàâíà ãðàäóñíàÿ ìåðà óãëà α, êîãäà ãðàäóñíàÿ ìåðà ñìåæíîãî åìó óãëà = 70°?
Êàê íàéòè ñìåæíûé óãîë?
Ðåøåíèå. Èç òåîðåìû î ñìåæíûõ óãëàõ íàõîäèì:

Äàëåå

Îòâåò.

Äîïîëíèòåëüíûå ìàòåðèàëû ïî òåìå: Óãëû. Ñìåæíûå óãëû.
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
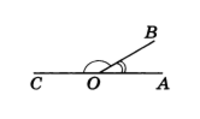
Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
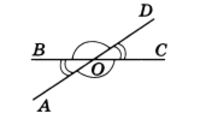
Вертикальные углы равны
Рис.2
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
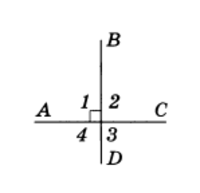
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
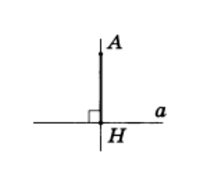
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
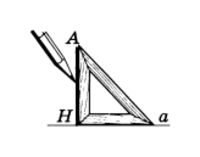
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Найдите величину угла ABC . Ответ дайте в градусах.

Геометрия
7 класс
Урок № 6
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
- Понятие смежных и вертикальных углов
- Свойства смежных и вертикальных углов
- Отличие аксиомы от теоремы
Тезаурус
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
- Сумма смежных углов равна 1800.
- Если два угла равны, то и смежные с ними углы равны.
- Угол, смежный с прямым углом, есть прямой угол.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Основная литература:
- Атанасян Л. С. Геометрия: 7 – 9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Погорелов А. В. Геометрия: 7 – 9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Обратите, внимание, что смежные углы АОВ и ВОС лежат на развёрнутом угле АОС. Отсюда можно сделать вывод: сумма смежных углов равна 180о.
Свойство смежных углов: сумма смежных углов равна 180о.
Давайте докажем это свойство.
Доказательство. Пусть углы ∠АОВ и ∠ВОС – смежные, луч ОВ – проходит между сторонами развёрнутого угла ∠АОС. Поэтому, сумма углов ∠АОВ и ∠ВОС равна ∠АОС, а этот угол развёрнутый, он равен 180о. Свойство доказано.
Укажем ещё одно свойство смежных углов.
- Если два угла равны, то и смежные с ними углы равны.
Сейчас давайте вспомним определение прямого угла: угол, равный 900, называется прямым углом. Опираясь на свойство суммы смежных углов, можно сделать вывод: угол, смежный с прямым углом, есть прямой угол.

Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.

Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
∠1+ ∠2= 1800 и ∠3+ ∠2= 1800. Получаем, что ∠1+ ∠2= ∠3+ ∠2, значит, ∠1= ∠3. Углы ∠1 и ∠3 – вертикальные. Мы доказали справедливость этого свойства.
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.

Ответ: ∠ВОК=____0
Решение. Воспользуемся свойством смежных углов: сумма смежных углов равна 1800. По условию задачи ∠АОК= 110, то ∠ВОК+ ∠АОК= 1800
∠ВОК+ 110= 1800
∠ВОК= 1800– 110= 1690.
Ответ: ∠ВОК= 1690
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.

Варианты ответов:
- 1120
- 640
- 1160
- 680
Решение. На чертеже указано, что углы ∠СОЕ= ∠DOE. Значит, ∠COD= ∠СОЕ+ ∠DOE= 320+ 320= 640. ∠AOD смежный с углом ∠COD, по свойству смежных углов: ∠AOD= 1800–∠COD= 1800– 640=1160.
Ответ: 1160
№3. Тип задания: выделение цветом.
Используя чертёж, найдите градусную меру угла ∠BMD, если ∠AMD= 1250, ∠BMC= 1150.
∠BМD=____0.
Выделите верный ответ из списка:
600; 300; 750; 900

Решение. По чертежу можно увидеть, что ∠BМD является частью ∠AMD и ∠BMC. Рассмотрим ∠DMC и ∠AMD. Эти углы – смежные, т.е. их сумма равна 1800. Значит, зная градусную меру ∠AMD, мы сможем найти градусную меру ∠DMC= 1800–∠AMD= 1800-–1250= 550. Теперь рассмотрим ∠BMC= ∠BMD+ ∠DMC. Мы знаем градусные меры ∠BMC и ∠DMC, значит, мы сможем найти градусную меру ∠BMD.
∠BMD= ∠BMC–∠DMC= 1150– 550= 600.
Верный ответ: 600
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Óãîë. Îñíîâíûå ïîíÿòèÿ. | |
| Êîãäà äâà ëó÷à ( AO è OB ) èñõîäÿò èç îäíîé òî÷êè, òî ôèãóðà, ñôîðìèðîâàííàÿ ýòèìè ëó÷àìè (âìåñòå ñ ÷àñòüþ ïëîñêîñòè, îãðàíè÷åííîé èìè), íàçûâàåòñÿ óãëîì. | |
| Óãîë. Îñíîâíûå ïîíÿòèÿ. | |
Ðàäèàíû. Ðàäèàííàÿ ìåðà óãëà. | |
| Ðàäèàííàÿ ìåðà. Êàê èçâåñòíî èç ïëàíèìåòðèè, äëèíà äóãè l, ðàäèóñ r è ñîîòâåòñòâóþùèé öåíòðàëüíûé óãîë α ñâÿçàíû ñîîòíîøåíèåì. | |
| Ðàäèàíû. Ðàäèàííàÿ ìåðà óãëà. | |
Óãëîâîé êîýôôèöèåíò. | |
| Óãëîâîé êîýôôèöèåíò — êîýôôèöèåíò k â óðàâíåíèè ïðÿìîé íà ïëîñêîñòè y = kx + b . | |
| Óãëîâîé êîýôôèöèåíò. | |
Óãëû. Ãðàäóñíàÿ ìåðà óãëà. | |
| Ãðàäóñíîé ìåðîé óãëà ÿâëÿåòñÿ ÷èñëî áîëüøå íóëÿ, êîòîðîå ïîêàçûâàåò, êàêîå ÷èñëî ðàç ãðàäóñ è åãî ÷àñòè — ìèíóòà è ñåêóíäà — ïîìåùàþòñÿ â ýòîì óãëå. | |
| Óãëû. Ãðàäóñíàÿ ìåðà óãëà. | |
Óãëû. Ñìåæíûå óãëû. | |
| Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ. | |
| Óãëû. Ñìåæíûå óãëû. | |
Óãîë. Âïèñàííûé óãîë. | |
| Âïèñàííûé óãîë – ýòî óãîë, ñôîðìèðîâàííûé äâóìÿ õîðäàìè , áåðóùèìè íà÷àëî â îäíîé òî÷êè îêðóæíîñòè. | |
| Óãîë. Âïèñàííûé óãîë. | |
Óãîë. Èçìåðåíèå óãëîâ. | |
| Èçìåðåíèå óãëîâ ñâîäèòñÿ ê èçìåðåíèþ ñîîòâåòñòâóþùèõ èì äóã ñëåäóþùèì îáðàçîì. | |
| Óãîë. Èçìåðåíèå óãëîâ. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
