Какие углы называются вертикальными какими свойствами они обладают
Медвед 7 лет назад Вертикальными называются углы, образованные пересекающимися прямыми и не являющиеся прилегающими друг к другу, то есть общей стороны у них нет, но вертикальные углы имеют вершину в одной точке. Вертикальные углы равны между собой. автор вопроса выбрал этот ответ лучшим Lalique 3 года назад Изучая школьный курс геометрии, мы знаем что есть вертикальные и смежные углы. Вертикальные углы довольно просто получить построением. Рисуем два луча, которые имеют точку пересечения. Теперь мы видим, что образовалось четыре угла. Те углы, которые будут симметричны относительно центра — именуют вертикальными. У этих углов есть одно главное свойство: они равны по величине. Знание этого равенства позволяет решить различные геометрические задачи неугомонная 4 года назад Вертикальные углы. Нарисовали две скрещенные прямые. Углы напротив друг друга будут вертикальными. Они касаются в одной точке в вершине. Прямая дает сторону углу одному и сторону углу другому. Получается четрые всего угла. Пара противоположных углов является вертикальными. TextExpert 3 года назад Это два угла, имеющие одну вершину — у двух пересекающихся прямых отрезков это два противоположных угла, где сторона одного есть продолжение стороны другого угла. Естественно, что такие углы будут равны друг с другом. Сashshi 7 лет назад Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны. Так же они в сумме дают девяносто градусов. Что мешает вам просто открыть учебник — все еще загадка для меня. Знаете ответ? |
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
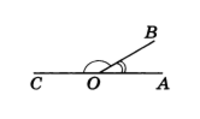
Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны
Рис.2
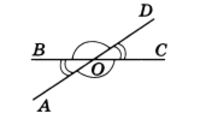
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
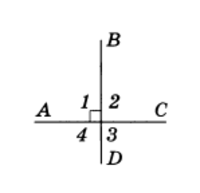
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
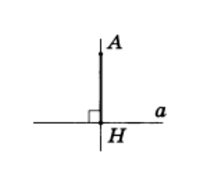
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
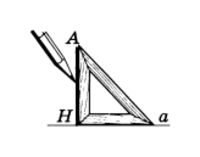
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Найдите величину угла ABC . Ответ дайте в градусах.

Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Óãîë. Îñíîâíûå ïîíÿòèÿ. | |
| Êîãäà äâà ëó÷à ( AO è OB ) èñõîäÿò èç îäíîé òî÷êè, òî ôèãóðà, ñôîðìèðîâàííàÿ ýòèìè ëó÷àìè (âìåñòå ñ ÷àñòüþ ïëîñêîñòè, îãðàíè÷åííîé èìè), íàçûâàåòñÿ óãëîì. | |
| Óãîë. Îñíîâíûå ïîíÿòèÿ. | |
Ðàäèàíû. Ðàäèàííàÿ ìåðà óãëà. | |
| Ðàäèàííàÿ ìåðà. Êàê èçâåñòíî èç ïëàíèìåòðèè, äëèíà äóãè l, ðàäèóñ r è ñîîòâåòñòâóþùèé öåíòðàëüíûé óãîë α ñâÿçàíû ñîîòíîøåíèåì. | |
| Ðàäèàíû. Ðàäèàííàÿ ìåðà óãëà. | |
Óãëîâîé êîýôôèöèåíò. | |
| Óãëîâîé êîýôôèöèåíò — êîýôôèöèåíò k â óðàâíåíèè ïðÿìîé íà ïëîñêîñòè y = kx + b . | |
| Óãëîâîé êîýôôèöèåíò. | |
Óãëû. Ãðàäóñíàÿ ìåðà óãëà. | |
| Ãðàäóñíîé ìåðîé óãëà ÿâëÿåòñÿ ÷èñëî áîëüøå íóëÿ, êîòîðîå ïîêàçûâàåò, êàêîå ÷èñëî ðàç ãðàäóñ è åãî ÷àñòè — ìèíóòà è ñåêóíäà — ïîìåùàþòñÿ â ýòîì óãëå. | |
| Óãëû. Ãðàäóñíàÿ ìåðà óãëà. | |
Óãëû. Ñìåæíûå óãëû. | |
| Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ. | |
| Óãëû. Ñìåæíûå óãëû. | |
Óãîë. Âïèñàííûé óãîë. | |
| Âïèñàííûé óãîë – ýòî óãîë, ñôîðìèðîâàííûé äâóìÿ õîðäàìè , áåðóùèìè íà÷àëî â îäíîé òî÷êè îêðóæíîñòè. | |
| Óãîë. Âïèñàííûé óãîë. | |
Óãîë. Èçìåðåíèå óãëîâ. | |
| Èçìåðåíèå óãëîâ ñâîäèòñÿ ê èçìåðåíèþ ñîîòâåòñòâóþùèõ èì äóã ñëåäóþùèì îáðàçîì. | |
| Óãîë. Èçìåðåíèå óãëîâ. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |

