Какие углы называют смежными вертикальными назовите их свойства
Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ.
Êàêèå óãëû íàçûâàþòñÿ ñìåæíûìè?
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ. Äëÿ óãëà 135 ãðàäóñîâ ñìåæíûì áóäåò óãîë ðàâíûé 45 ãðàäóñàì. Äëÿ óãëà x ãðàäóñîâ ñìåæíûì ÿâëÿåòñÿ óãîë (180 – x) ãðàäóñîâ. |  |
Äâà ñìåæíûõ óãëà — ýòî óãëû, ñ îäíîé îáùåé ñòîðîíîé, à îñòàëüíûå ñòîðîíû íàõîäÿòñÿ íà îäíîé ïðÿìîé.
Ïðè ïåðåñå÷åíèè 2-õ ïðÿìûõ ïîëó÷àåòñÿ 4-ðå ïàðû ñìåæíûõ óãëîâ:
∠1 è ∠2, ∠3 è ∠4, ∠1 è ∠3, ∠2 è ∠4 Íî, òàê êàê ∠1 =∠4, ∠2 = ∠3 (êàê âåðòèêàëüíûå), òî äîñòàòî÷íî ðàññìàòðèâàòü òîëüêî îäíó èç ýòèõ ïàð. |  |
Ñâîéñòâî ñìåæíûõ óãëîâ.
×åìó ðàâíà ñóììà ñìåæíûõ óãëîâ?
Ñìåæíûå óãëû ðàâíû: ñóììà ñìåæíûõ óãëîâ 180º.
1. α+ β= 180°
2. α= 180°−β
Ñëåäñòâèÿ èç òåîðåìû î ñìåæíûõ óãëàõ.
- Åñëè 2 óãëà ðàâíû, òî ñìåæíûå èì óãëû òîæå ðàâíû.
- Åñëè óãîë íå ðàçâåðíóòûé, çíà÷èò îí ≠180°.
- Ñìåæíûé óãîë äëÿ ïðÿìîãî óãëà (ò.å. óãëà, ó íåãî ãðàäóñíàÿ ìåðà = 90°), òîæå ïðÿìîé.
- Ñìåæíûé óãîë äëÿ îñòðîãî óãëà (ãðàäóñíàÿ ìåðà ìåíüøå 90°), áóäåò òóïûì (ãðàäóñíàÿ ìåðà áîëüøå
90°), à ñìåæíûé òóïîìó — îñòðûì.
Òðèãîíîìåòðè÷åñêèå ñîîòíîøåíèÿ.
- Ñèíóñû ñìåæíûõ óãëîâ îäèíàêîâû. Èõ êîñèíóñû è òàíãåíñû ðàâíû ïî âåëè÷èíå, íî èìåþò
ïðîòèâîïîëîæíûå çíàêè (èñêëþ÷åíèå íåîïðåäåëåííûå çíà÷åíèÿ).
- ×òîáû ïîñòðîèòü óãîë, ñìåæíûé ñóùåñòâóþùåìó, íåîáõîäèìî îäíó èç ñòîðîí íàøåãî óãëà ïðîäëèòü
äàëüøå âåðøèíû.

Ðàññìîòðèì ïðèìåð:
Çàäàíèå. ×åìó áóäåò ðàâíà ãðàäóñíàÿ ìåðà óãëà α, êîãäà ãðàäóñíàÿ ìåðà ñìåæíîãî åìó óãëà = 70°?
Êàê íàéòè ñìåæíûé óãîë?
Ðåøåíèå. Èç òåîðåìû î ñìåæíûõ óãëàõ íàõîäèì:

Äàëåå

Îòâåò.

Äîïîëíèòåëüíûå ìàòåðèàëû ïî òåìå: Óãëû. Ñìåæíûå óãëû.
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
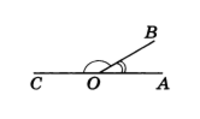
Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
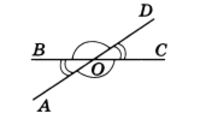
Вертикальные углы равны
Рис.2
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
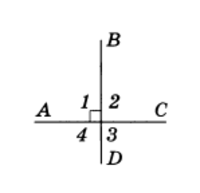
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
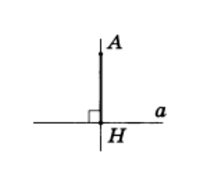
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
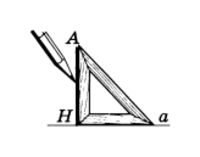
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Найдите величину угла ABC . Ответ дайте в градусах.

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
