Какие свойством обладает окружность

Окружность — это множество точек на плоскости, равноудаленных от некоторой точки этой же плоскости, называемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.
Свойства окружности
- Среди всех замкнутых линий заданной длины окружность ограничивает участок плоскости наибольшей площади.
- Окружность является простой плоской кривой второго порядка.
- Окружность есть геометрическое место точек, сумма квадратов расстояний от которых до нескольких заданных точек постоянна.
- Окружность есть геометрическое место точек, отношение расстояний от которых до двух данных точек А и В постоянно и не равно 1.
Окружность и симметрии
- Кривизна окружности одинакова во всех точках.
- Окружность переходит сама в себя при любых поворотах относительно центра.
- Окружность обладает центральной симметрией относительно своего центра.
- Окружность обладает зеркальной симметрией относительно любого из своих диаметров.
- Окружность является кривой постоянной ширины (длина проекции окружности на любую лежащую в ее плоскости ось одинакова и равна диаметру).
Окружность и точки
- Через три точки, не лежащие на одной прямой, можно провести окружность, и причем только одну.
- Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
- При любом расположении двух равных окружностей на плоскости они имеют не больше двух общих точек.
- Точка касания двух окружностей лежит на прямой, проходящей через их центры.
Окружность и прямые
- Касательная к окружности в любой точке перпендикулярна радиусу, проведенному в эту точку.
- Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
- Диаметр, перпендикулярный к хорде окружности, делит эту хорду и обе стягиваемые ею дуги пополам.
- Дуги, заключенные между параллельными хордами, равны.
- Короткие и длинные отрезки двух пересекающиеся хорд окружности соотносятся в одинаковой пропорции.
Окружность и треугольники
- Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника.
- Центр описанной вокруг треугольника окружности лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
- Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине его гипотенузы.
- Центры описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный.
Окружность и четырехугольники
- Около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°.
- В четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон.
- Вокруг параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником.
- В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
- Вокруг трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная.
- Центр окружности, описанной вокруг равнобедренной трапеции, лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне.
Источники:
- ru.wikipedia.org — Википедия: Окружность. Свойства;
- univer.omsk.su — окружность и ее свойства;
- kvant.mirror1.mccme.ru — «Калейдоскоп «Кванта»: свойства и признаки окружности (PDF).
Дополнительно на Геноне:
- Что такое окружность? Что такое диаметр окружности? Что такое радиус окружности? Как найти радиус окружности? Как вычислить длину окружности? Как найти площадь круга? (в одном ответе)
- Чем отличается круг от окружности?
- Как выглядит уравнение окружности?
- Как найти радиус вписанной в треугольник окружности?
- Как найти радиус описанной вокруг треугольника окружности?
Окружностью
называется фигура, состоящая из всех точек плоскости, находящихся от
данной точки на данном расстоянии. Данная точка называется центром окружности,
а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом
окружности.
Часть плоскости, ограниченная окружностью называется кругом.
Круговым сектором или просто сектором называется часть
круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с
центром круга.
Сегментом называется часть круга, ограниченная дугой и стягивающей
ее хордой.
Основные термины
Касательная
Прямая, имеющая с только одну общую точку, называется касательной
к окружности, а их общая точка называется точкой касания прямой
и окружности.
Свойства касательной
- Касательная к окружности перпендикулярна к радиусу, проведенному в
точку касания. - Отрезки касательных к окружности, проведенных из одной точки, равны
и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Хорда
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд
- Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые
ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит
пополам хорду, то он перпендикулярен этой хорде. - Дуги, заключенные между параллельными хордами, равны.
- Если две хорды окружности, AB и CD пересекаются в точке
M, то произведение отрезков одной хорды равно произведению отрезков
другой хорды: AM•MB = CM•MD.
Свойства окружности
- Прямая может не иметь с окружностью общих точек; иметь с окружностью
одну общую точку (касательная); иметь с ней
две общие точки (секущая). - Через три точки, не лежащие на одной прямой, можно провести окружность,
и притом только одну. - Точка касания двух окружностей лежит на линии, соединяющей их центры.
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная
и секущая, то квадрат длины касательной равен произведению
секущей на ее внешнюю часть: MC2 = MA•MB.
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие,
то произведение одной секущей на её внешнюю часть равно произведению другой
секущей на её внешнюю часть. MA•MB = MC•MD.
Углы
в окружности
Центральным углом в окружности называется плоский угол с вершиной
в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту
окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей
называется дугой окружности. Мерой дуги может служить мера соответствующего
ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её
концы, является диаметром.
Свойства углов, связанных с окружностью
- Вписанный угол либо равен половине соответствующего ему центрального
угла, либо дополняет половину этого угла до 180°. - Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу,
равны. - Вписанный угол, опирающийся на диаметр, равен
90°. - Угол, образованный касательной к окружности и
секущей, проведенной через точку касания, равен половине
дуги, заключенной между его сторонами.
Длины и площади
- Длина окружности C радиуса R вычисляется
по формуле: - Площадь S круга радиуса R вычисляется
по формуле: - Длина дуги окружности L радиуса R с центральным углом
,измеренным
в радианах, вычисляется по формуле: - Площадь S сектора радиуса R с центральным
углом в
радиан вычисляется по формуле:
C = 2 R.
S = R2.
L = R .
S = R2
.
Вписанные и описанные окружности
Окружность и треугольник
- центр вписанной окружности — точка пересечения
биссектрис треугольника,
ее радиус r вычисляется по формуле: - центр описанной окружности — точка пересечения
серединных перпендикуляров,
ее радиус Rвычисляется по формуле: - центр описанной около прямоугольного
треугольника окружности лежит на середине гипотенузы; - центр описанной и вписанной окружностей треугольника совпадают только
в том случае, когда этот треугольник — правильный.
r = ,
где S — площадь треугольника, а —
полупериметр;
R =
,
R = ;
здесь a, b, c — стороны треугольника,
— угол, лежащий против стороны a, S — площадь треугольника;
Окружность и четырехугольники
- около параллелограмма можно
описать окружность тогда и только тогда, когда он является прямоугольником; - около трапеции
можно описать окружность тогда и только тогда, когда эта трапеция
— равнобедренная; центр
окружности лежит на пересечении оси симметрии трапеции
с серединным перпендикуляром
к боковой стороне; - в параллелограмм можно вписать
окружность тогда и только тогда, когда он является ромбом.
§ 20. Некоторые свойства окружности. Касательная к окружности

Теорема 20.1
Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Рис. 287 |
|
Доказательство
Если хорда является диаметром, то теорема очевидна.
На рисунке 287 изображена окружность с центром O, M — точка пересечения диаметра CD и хорды AB, CD ⊥ AB. Надо доказать, что AM = MB.
Проведём радиусы OA и OB. В равнобедренном треугольнике AOB (OA = OB) отрезок OM — высота, а значит, и медиана, т. е. AM = MB. 

Теорема 20.2
Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.
На рисунке 288 показаны все возможные случаи взаимного расположения прямой и окружности. На рисунке 288, а они не имеют общих точек, на рисунке 288, б — имеют две общие точки, на рисунке 288, в — одну.

Определение
Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 288, в прямая a — касательная к кругу с центром в точке O, A — точка касания.
Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 289 изображён отрезок AB, который касается окружности в точке С.

Теорема 20.3
(свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Доказательство
На рисунке 290 изображена окружность с центром O, A — точка касания прямой a и окружности. Надо доказать, что OA ⊥ a.
Рис. 289 | Рис. 290 | Рис. 291 |
|
|
|
Предположим, что это не так, т. е. отрезок OA — наклонная к прямой a. Тогда из точки O опустим перпендикуляр OM на прямую a (рис. 291). Поскольку точка A — единственная общая точка прямой a и круга с центром O, то точка M не принадлежит этому кругу. Отсюда OM = MB + OB, где точка B — точка пересечения окружности и перпендикуляра OM. Отрезки OA и OB равны как радиусы окружности. Таким образом, OM > OA. Получили противоречие: перпендикуляр OM больше наклонной OA. Следовательно, OA ⊥ a. 

Теорема 20.4
(признак касательной к окружности)
Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.
Доказательство
Рис. 292 |
|
На рисунке 290 изображена окружность с центром в точке O, отрезок OA — её радиус, точка A принадлежит прямой a, OA ⊥ a. Докажем, что прямая a — касательная к окружности.
Пусть прямая a не является касательной, а имеет ещё одну общую точку B с окружностью (рис. 292). Тогда ∆AOB — равнобедренный (OA = OB как радиусы). Отсюда ∠OBA = ∠OAB = 90°. Получаем противоречие: в треугольнике AOB есть два прямых угла. Следовательно, прямая a является касательной к окружности. 

Следствие
Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
Рис. 293 |
|
Докажите это следствие самостоятельно.

Задача. Докажите, что если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.
Решение. На рисунке 293 изображена окружность с центром O. Прямые AB и AC — касательные, точки B и C — точки касания. Надо доказать, что AB = AC.
Проведём радиусы OB и OC в точки касания. По свойству касательной OB ⊥ AB и OC ⊥ AC. В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC. 

- Как делит хорду диаметр, перпендикулярный ей?
- Чему равен угол между хордой, отличной от диаметра, и диаметром, делящим эту хорду пополам?
- Опишите все возможные случаи взаимного расположения прямой и окружности.
- Какую прямую называют касательной к окружности?
- Каким свойством обладает радиус, проведённый в точку касания прямой и окружности?
- Сформулируйте признак касательной к окружности.
- Каким свойством обладают касательные, проведённые к окружности через одну точку?

Практические задания

507.Начертите окружность с центром O, проведите хорду AB. Пользуясь угольником, разделите эту хорду пополам.
508.Начертите окружность с центром O, проведите хорду CD. Пользуясь линейкой со шкалой, проведите диаметр, перпендикулярный хорде CD.
509.Начертите окружность, отметьте на ней точки A и B. Пользуясь линейкой и угольником, проведите прямые, которые касаются окружности в точках A и B.
510.Проведите прямую a и отметьте на ней точку M. Пользуясь угольником, линейкой и циркулем, проведите окружность радиуса 3 см, которая касается прямой a в точке M. Сколько таких окружностей можно провести?

Упражнения

511.На рисунке 294 точка O — центр окружности, диаметр CD перпендикулярен хорде AB. Докажите, что ∠AOD = ∠BOD.
512.Докажите, что равные хорды окружности равноудалены от её центра.
513.Докажите, что если хорды окружности равноудалены от её центра, то они равны.
514.Верно ли, что прямая, перпендикулярная радиусу окружности, касается этой окружности?
515.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠BAD = 35° (рис. 295). Найдите ∠AOB.
516.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠AOB = 80° (см. рис. 295). Найдите ∠BAC.
517.Дана окружность, диаметр которой равен 6 см. Прямая a удалена от её центра на: 1) 2 см; 2) 3 см; 3) 6 см. В каком случае прямая a является касательной к окружности?
518.В треугольнике ABC известно, что ∠C = 90°. Докажите, что:
1)прямая BC является касательной к окружности с центром A, проходящей через точку C;
2)прямая AB не является касательной к окружности с центром C, проходящей через точку A.

519.Докажите, что диаметр окружности больше любой хорды, отличной от диаметра.
520.В окружности с центром O через середину радиуса провели хорду AB, перпендикулярную ему. Докажите, что ∠AOB = 120°.
521.Найдите угол между радиусами OA и OB окружности, если расстояние от центра O окружности до хорды AB в 2 раза меньше: 1) длины хорды AB; 2) радиуса окружности.
522.В окружности провели диаметр AB и хорды AC и CD так, что AC = 12 см, ∠BAC = 30°, AB ⊥ CD. Найдите длину хорды CD.
523.Через точку M к окружности с центром O провели касательные MA и MB, A и B — точки касания, ∠OAB = 20°. Найдите ∠AMB.
524.Через концы хорды AB, равной радиусу окружности, провели две касательные, пересекающиеся в точке C. Найдите ∠ACB.
525.Через точку C окружности с центром O провели касательную к этой окружности, AB — диаметр окружности. Из точки A на касательную опущен перпендикуляр AD. Докажите, что луч AC — биссектриса угла BAD.
526.Прямая AC касается окружности с центром O в точке A (рис. 296). Докажите, что угол BAC в 2 раза меньше угла AOB.
Рис. 294 | Рис. 295 | Рис. 296 |
|
|
|
527.Отрезки AB и BC — соответственно хорда и диаметр окружности, ∠ABC = 30°. Через точку A провели касательную к окружности, пересекающую прямую BC в точке D. Докажите, что ∆ABD — равнобедренный.
528.Известно, что диаметр AB делит хорду CD пополам, но не перпендикулярен ей. Докажите, что CD — также диаметр.

529.Найдите геометрическое место центров окружностей, которые касаются данной прямой в данной точке.
530.Найдите геометрическое место центров окружностей, которые касаются обеих сторон данного угла.
531.Найдите геометрическое место центров окружностей, которые касаются данной прямой.
532.Прямые, касающиеся окружности с центром O в точках A и B, пересекаются в точке K, ∠AKB = 120°. Докажите, что AK + BK = OK.
533.Окружность касается стороны AB треугольника ABC в точке M и касается продолжения двух других сторон. Докажите, что сумма длин отрезков BC и BM равна половине периметра треугольника ABC.
Рис. 297 |
|
534.Через точку C проведены касательные AC и BC к окружности, A и B — точки касания (рис. 297). На окружности взяли произвольную точку M, лежащую в одной полуплоскости с точкой C относительно прямой AB, и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметр треугольника DEC не зависит от выбора точки M.

Упражнения для повторения
535.Докажите, что середина M отрезка, концы которого принадлежат двум параллельным прямым, является серединой любого отрезка, который проходит через точку M и концы которого принадлежат этим прямым.
536.Отрезки AB и CD лежат на одной прямой и имеют общую середину. Точку M выбрали так, что треугольник AMB — равнобедренный с основанием AB. Докажите, что ∆CMD также является равнобедренным с основанием CD.
537.На стороне MK треугольника MPK отметили точки E и F так, что точка E лежит между точками M и F, ME = EP, PF = FK. Найдите угол M, если ∠EPF = 92°, ∠K = 26°.
538.В остроугольном треугольнике ABC проведена биссектриса BM, из точки M на сторону BC опущен перпендикуляр MK, ∠ABM = ∠KMC. Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте
539.Установите закономерность форм фигур, изображённых на рисунке 298. Какую фигуру надо поставить следующей?
Рис. 298 |
|
Окружность — это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости на заданное расстояние (рисунок 1).
Круг — часть плоскости, которая ограниченна окружностью (рисунок 1).
Другое понятие круга.
Круг — это часть плоскости, которая лежит внутри окружности, вместе с самой окружностью (рисунок 1).
Рисунок 1
Радиус r — это любой отрезок, соединяющий центр окружности и точку окружности. На рисунке 2 это отрезок OC.
Также радиус от лат. называли спицу в колесе.
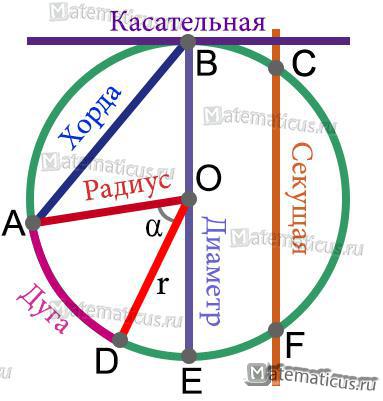
Рисунок 2
Хорда — это отрезок AB, соединяющий две точки окружности (рисунок 2).
Диаметр — это хорда BE, проходящая через цент окружности (рисунок 2).
Если на окружности взять две точки, то они разобьют окружность на две части (рисунок 2). Каждая из этих кривых называется дугой окружности, а точки A и D — концы этих дуг.
Дуга обозначается как ∪ AD (рисунок 2).
Длина дуги окружности ∪AB (рисунок 3) находится по формуле:
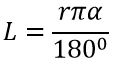
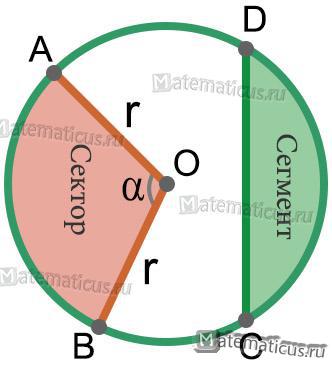
Рисунок 3
Сектор круга — это часть плоскости, ограниченная двумя радиусами и его дугой (рисунок 3).
Площадь сектора, формула:
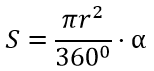
Сегмент круга — это часть плоскости, ограниченная хордой и дугой (рисунок 3).
Площадь сектора окружности, формула:
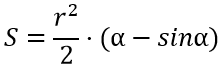
Касательной называется прямая a, имеющая с окружностью только одну общую точку A (рисунок 5).
Формула для расчета длины окружности через радиус:
L=2πr
Формула для расчета длины окружности через диаметр:
L=2πd
Формула для определения площади круга через радиус:
S=πR2
Формула для определения площади круга через диаметр: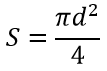
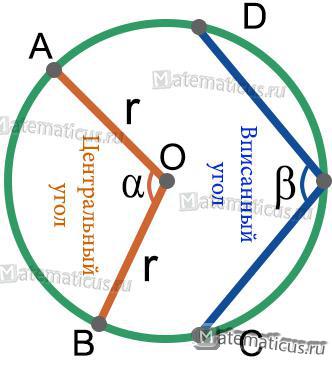
Рисунок 4
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Формула для определения длины хорды ∪ AB через радиус и центральный угол ∠BOA:
AB=2rsin α/2
Формула для определения длины хорды через радиус и вписанный угол ∠CED:
CD=2rsinα
Свойства касательной к окружности
Одно из свойств касательной к окружности (рисунок 5) заключается в том, что касательная a к окружности перпендикулярна ее радиусу OA. Из этого вытекает аналогичное свойство, т.е. касательная , проходящая через точку касания с окружностью, перпендикулярна диаметру.
OA⊥a
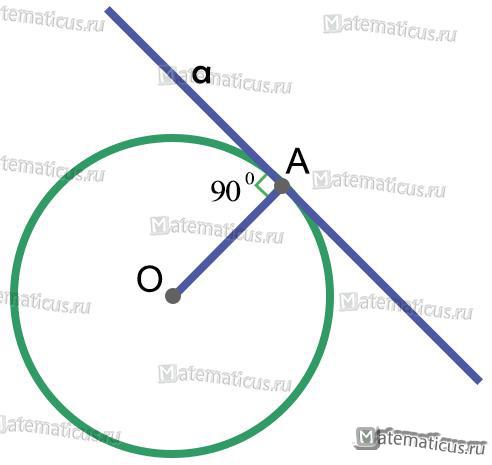
Рисунок 5
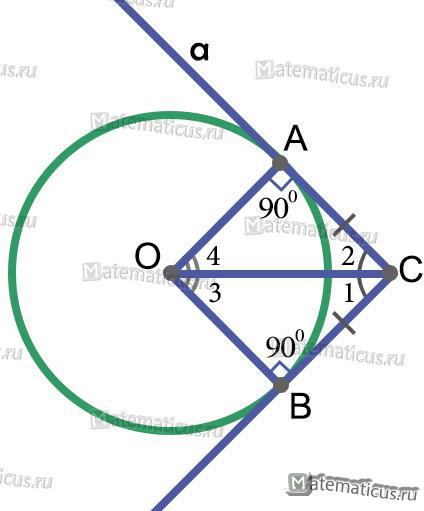
Рисунок 6
CA, CB – касательные
A, B – точки касания
CA = CB
В соответствии с рисунком 6, получаем свойство
∠1 = ∠2; ∠3 = ∠4
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойства секущей окружности
Секущая окружности — это прямая BE, имеющая с окружностью две общие точки (рисунок 7).
В соответствии с рисунком 7, получаем свойство
BA2=BF⋅BD
BA2=BE⋅BC
где AB — касательная
BE, BF — секущие
Из этого свойства вытекает следующее свойство, произведения отрезков секущих, проведенных из одной точки равны:
BF⋅BD=BE⋅BC
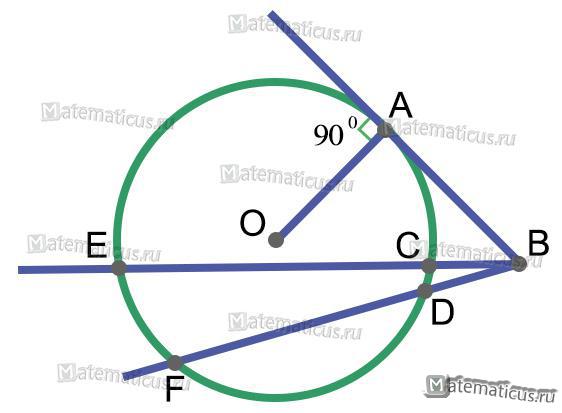
Рисунок 7
Свойства окружности
- Диаметр окружности равен сумме двух радиусов, то есть
d =r+r=2·r
- Через три точки, не лежащих на одной прямой, можно построить только единственную окружность.
- Если взять все замкнутые кривые с одинаковой длиной, то окружность имеет максимальную величину площади.
Кратчайшее расстояние от центра окружности к секущей или хорде всегда меньше величины радиуса.
- Если две окружности соприкасаются внешне или внутренне в одной точке, то точка касания и центры этих окружностей лежат на одной прямой.
Свойства углов окружности
На рисунке 8
∪ CB — дуга окружности
∠COB — центральный угол
∠CAB — вписанный угол
Получаем следующее тождество:
∠CAB = ∠COB/2
при этом длина дуги окружности ∪ CB должна быть меньше длины полуокружности.
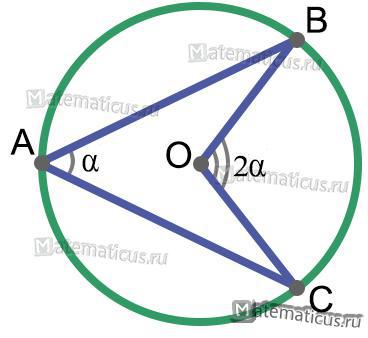
Рисунок 8
Вписанные углы, опирающиеся на одну и ту же дугу, равны (рисунок 9).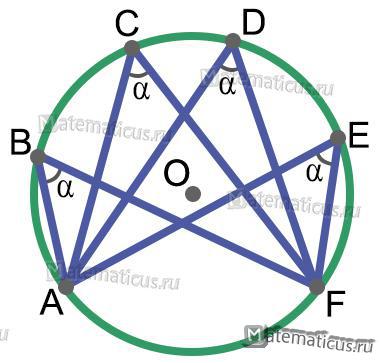
Рисунок 9
Вписанный угол, опирающийся на полуокружность – прямой (рисунок 10).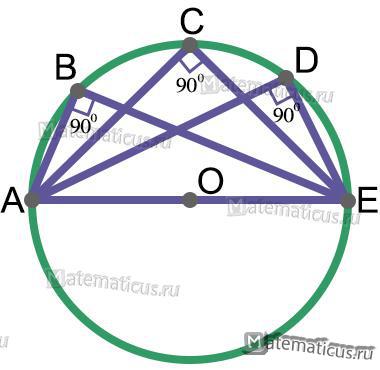
Рисунок 10
Свойство хорд окружности
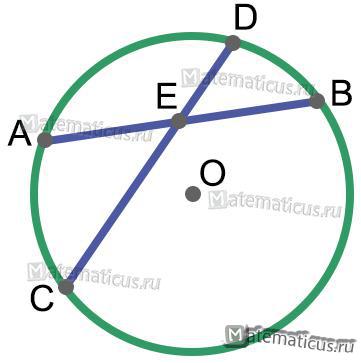
Рисунок 11
AB; CD – хорды
E — точка пересечения хорд
AE · EB = CE · ED
Если две хорды окружности пересекаются, то произведение отрезков одной хорды AB равно произведению отрезков другой хорды CD
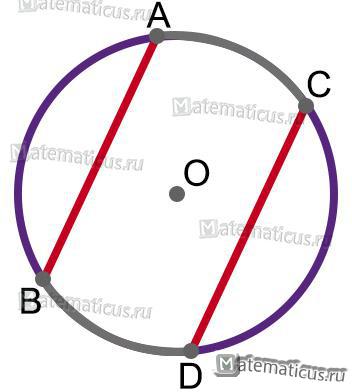
Рисунок 12
Если хорда AB равна хорде DC, то их дуги тоже равны, т.е.
AB=DC ⇒ ∪AB=∪DC
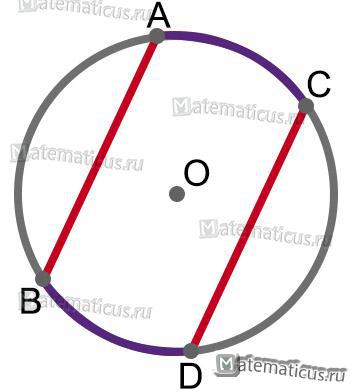
Рисунок 13
Если хорда AB параллельна хорде DC, то их дуги равны, т.е.
AB//DC ⇒ ∪AB=∪DC
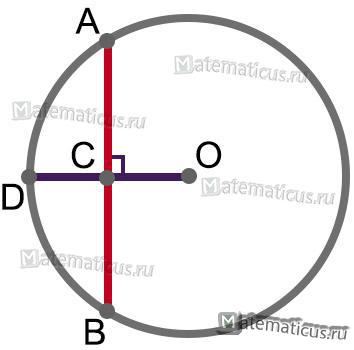
Рисунок 14
Если радиус окружности OD перпендикулярен хорде AB, то он делит хорду пополам в точке их пересечения С, т.е.
OD⊥AB ⇒ ∪AC=∪BC
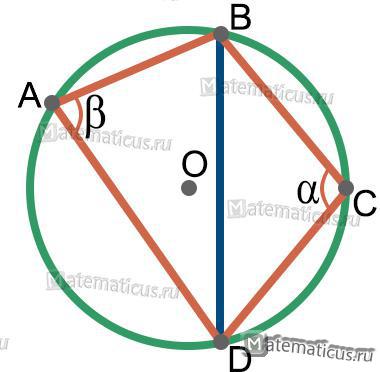
Рисунок 15
Сумма двух вписанных углов, опирающих на одну хорду и находящихся по разные стороны от нее, равна 180°, т.е.
α + β = 180°
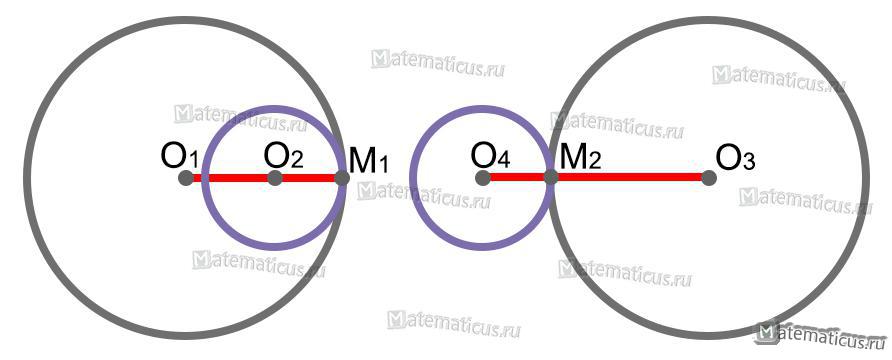
Рисунок 16











