Какие свойства у пропорции
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение ![]() равно отношению
равно отношению ![]()
![]()
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
![]()
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
![]()
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение ![]() пропорционально отношению
пропорционально отношению ![]() . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
. Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что ![]() , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение ![]() не пропорционально отношению
не пропорционально отношению ![]() .
.
![]()
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция ![]() состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была ![]() . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями
. Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями ![]() и
и ![]() знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
![]()
2 = 2
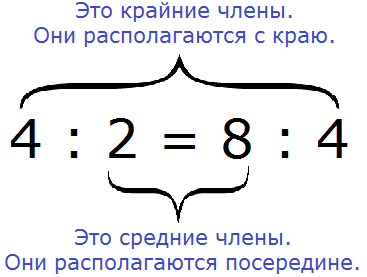
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции ![]() крайние члены это 4 и 4, а средние члены это 2 и 8
крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
![]()
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция ![]() . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
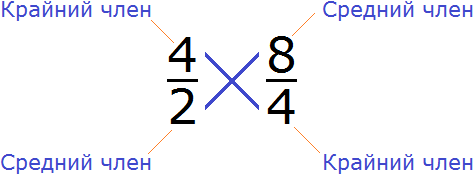
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция ![]() составлена правильно.
составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция ![]()
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
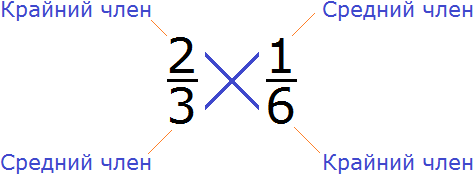
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция ![]() составлена неправильно.
составлена неправильно.
Поэтому в пропорции ![]() разумнее заменить знак равенства (=) на знак не равно (≠)
разумнее заменить знак равенства (=) на знак не равно (≠)
![]()
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Навигация по записям
Ïîñêîëüêó 3,6 : 0,9 = 4 è 1,2 : 0,3 = 4, òî âåðíî è ðàâåíñòâî 3,6 : 0,9 = 1,2 : 0,3, êîòîðîå íàçûâàþò ïðîïîðöèåé (îò ëàò. ðãîðîrtio — «ñîèçìåðèìîñòü»).
Åñëè ñîîòíîøåíèå à : b ðàâíî ñîîòíîøåíèþ ñ : d, òî òîæäåñòâî à : b = ñ:d íàçûâàþò ïðîïîðöèåé.
Ïðîïîðöèþ ìîæíî âûðàçèòü òàêæå â âèäå:
Ïðèâåä¸ííûå çàïèñè ÷èòàþò: «ñîîòíîøåíèå à ê b ðàâíî ñîîòíîøåíèþ ñ ê d èëè «à ñîîòíîñèòñÿ ê b, êàê ñ ñîîòíîñèòñÿ ê d».
×èñëà a è d èìåíóþò êðàéíèìè ÷ëåíàìè ïðîïîðöèè, ÷èñëà b è ñ — ñðåäíèìè ÷ëåíàìè ïðîïîðöèè.
 ïðîïîðöèè 3,6 : 0,9 = 1,2 : 0,3 ÷èñëà 3,6 è 0,3 — êðàéíèå ÷ëåíû, ÷èñëà 0,9 è 1,2 — ñðåäíèå ÷ëåíû. Ðàññìîòðèì ïðîèçâåäåíèå êðàéíèõ è ñðåäíèõ ÷ëåíîâ 3,6•0,3 = 0,9 • 1,2
Òàêàÿ îñîáåííîñòü ïðèñóùà êàæäîé ïðîïîðöèè è èìåíóåòñÿ ãëàâíàÿ îñîáåííîñòü ïðîïîðöèè — ïðîèçâåäåíèå êðàéíèõ ÷ëåíîâ ïðîïîðöèè ðàâíî ïðîèçâåäåíèþ å¸ ñðåäíèõ ÷ëåíîâ.
Ýòî îïðåäåëÿåòñÿ òàê:
åñëè , òî ad = bc
Ãëàâíóþ îñîáåííîñòü ïðîïîðöèè åùå èìåíóþò ïðàâèëîì êðåñòà. Ñëåäóÿ ãëàâíîé îñîáåííîñòè ïðîïîðöèè, ìîæíî ðàññ÷èòàòü åå íåèçâåñòíûé ÷ëåí, åñëè âñå îñòàëüíûå ÷ëåíû îïðåäåëåíû.
×òîáû îïðåäåëèòü íåèçâåñòíûé êðàéíèé ÷ëåí ïðîïîðöèè, íåîáõîäèìî ïðîèçâåäåíèå ñðåäíèõ ÷ëåíîâ ïðîïîðöèè ïîäåëèòü íà èçâåñòíûé êðàéíèé ÷ëåí.
×òîáû îïðåäåëèòü íåèçâåñòíûé ñðåäíèé ÷ëåí ïðîïîðöèè, íåîáõîäèìî ïðîèçâåäåíèå êðàéíèõ ÷ëåíîâ ïðîïîðöèè ïîäåëèòü íà èçâåñòíûé ñðåäíèé ÷ëåí. Èëè îáîáùåííî ìîæíî ñôîðìóëèðîâàòü òàê: ÷òîáû âû÷èñëèòü íåèçâåñòíûé ÷ëåí ïðîïîðöèè, ñëåäóåò ïåðåìíîæèòü äèàãîíàëü ñ îáîèìè èçâåñòíûìè ÷ëåíàìè, à äàëåå ïîäåëèòü íà îñòàâøååñÿ èçâåñòíîå çíà÷åíèå.
Ïðàâèëüíà è ñëåäóþùàÿ ôîðìóëèðîâêà: åñëè à, b, ñ è d ÷èñëà îòëè÷íûå îò íóëÿ, òî äëÿ íèõ âåðíî:
åñëè , òî
ýòà îñîáåííîñòü íàçûâàåòñÿ ñâîéñòâîì îáðàùåíèÿ ïðîïîðöèè.
Åñëè â âåðíîé ïðîïîðöèè ïîìåíÿòü ìåñòàìè ñðåäíèå ÷ëåíû èëè
êðàéíèå ÷ëåíû, òî ïîëó÷èâøèåñÿ íîâûå ïðîïîðöèè òîæå âåðíû. Ýòî ñâîéñòâî ïåðåñòàíîâêè êðàéíèõ è ñðåäíèõ ÷ëåíîâ ïðîïîðöèè.
Åñëè , òî
(ïåðåñòàíîâêà ñðåäíèõ ÷ëåíîâ ïðîïîðöèè),
(ïåðåñòàíîâêà êðàéíèõ ÷ëåíîâ ïðîïîðöèè).
Òàê æå íà ïðàêòèêå ïîëüçóþòñÿ ïðàâèëîì óâåëè÷åíèÿ è óìåíüøåíèÿ ïðîïîðöèè.
Åñëè , òî ðàâåíñòâî ñîõðàíèòñÿ è â ñëåäóþùèõ ñëó÷àÿõ:
(óâåëè÷åíèå ïðîïîðöèè),
(óìåíüøåíèå ïðîïîðöèè).
Ñîñòàâëåíèå ïðîïîðöèè ñëîæåíèåì è âû÷èòàíèåì .
Åñëè , òî
(ñîñòàâëåíèå ïðîïîðöèè ñëîæåíèåì),
(ñîñòàâëåíèå ïðîïîðöèè âû÷èòàíèåì).
Îáðàòèì âíèìàíèå, ÷òî ñîñòàâëåíèå ïðîïîðöèé — åù¸ îäèí ñïîñîá ðåøåíèÿ çàäà÷ íà ïðîöåíòû.
Íàïðèìåð:
Îëîâî ïðîèçâîäÿò èç ìèíåðàëà, êîòîðûé íàçûâàþò êàññèòåðèòîì. Ñêîëüêî òîíí îëîâà ïîëó÷àò èç 25 ò êàññèòåðèòà, åñëè îí ñîäåðæèò 78 % îëîâà?
Ðåøåíèå. Ïóñòü ïîëó÷àò õ ò îëîâà. Âçÿâ ìàññó ìèíåðàëà çà 100 % , çàïèøåì:
25 ò — 100%
õ ò — 78 %.
Ðåøèâ 25•78 = 100õ ìû íàõîäèì, ÷òî õ = 19,5ò.
Êîíöåïöèÿ ïðîïîðöèè òåñíî âçàèìîñâÿçàíà ñ ïðîïîðöèîíàëüíîñòüþ. Ïðîïîðöèîíàëüíîñòü — ýòî íåèçìåííîå ñîîòíîøåíèå äâóõ âåëè÷èí äðóã ê äðóãó. Íàïðèìåð, ÷åì áîëüøå ìû äàâèì íà ïåäàëü «ãàç» â ìàøèíå, òåì ñòðåìèòåëüíåå îíà ïîåäåò.
Ïðîïîðöèîíàëüíîñòü ìîæåò áûòü ïðÿìîé è îáðàòíîé.
Ïðÿìàÿ ïðîïîðöèîíàëüíîñòü -ðîñò îäíîé âåëè÷èíû âëå÷åò çà ñîáîé ðîñò äðóãîé.
Îáðàòíàÿ ïðîïîðöèîíàëüíîñòü ñóùåñòâóåò òîãäà, êîãäà ðîñò îäíîé âåëè÷èíû â íåñêîëüêî ðàç, âî ñòîëüêî æå ðàç óìåíüøàåò äðóãóþ. Ïðîäîëæàÿ ïðåäûäóùèé ïðèìåð — îáðàòíàÿ ïðîïîðöèîíàëüíîñòü ìåæäó íàæàòèåì íà ïåäàëü «òîðìîç» è ñêîðîñòüþ àâòîìîáèëÿ — ÷åì áîëüøå ìû äàâèì íà òîðìîç, òåì ìåíüøå ñêîðîñòü.
Технологическая карта урока
Черненко Нина Николаевна, учитель математики МКОУ СОШ №2 г. Нижнеудинск
Предмет – Математика
Класс – 6
Тема урока: «Пропорция. Основное свойство пропорции»
Тип урока: Урок открытия новых знаний.
Цели урока:
Обучающие цели:
─ ввести понятие пропорции и её членов;
─ сформулировать основное свойство пропорции;
─ научить составлять пропорции из отношений.
Развивающие цели:
─ развивать умение анализировать и делать выводы;
─ развивать навыки самостоятельной исследовательской работы;
─ развивать грамотную математическую речь
Воспитательные цели:
─ воспитывать умение слушать друг друга;
─ воспитывать у учащихся интерес к предмету.
Образовательные технологии, используемые на уроке:
Информационно-коммуникационная (компьютерная демонстрация презентации к уроку);
Проблемно-диалоговая технология;
Здоровье сберегающая технология (физкультминутка, создание позитивного эмоционального настроя на работу всех учеников в ходе урока; организация различных форм деятельности учащихся,организация урока с учетом временного восприятия и усвоения учебного материала).
Формы работы учащихся:
Групповая – обсуждение и выведение правила: что такое пропорция, как называют числа в пропорции, основное свойство пропорции;
Фронтальная – ответы на вопросы, чтение пропорции, выделение крайних и средних членов пропорции, проверка верности пропорции;
Индивидуальная– выполнение заданий из учебника.
Методы обучения:
Словесные – беседа, рассказ;
Наглядные – демонстрация презентации;
Практические – решение задач, практическая работа
Необходимое оборудование и материалы для урока: компьютер, мультимедийный проектор, раздаточный материал, компьютерная презентация в MicrosoftPowerPoint.
Планируемые образовательные результаты: изучить понятия: пропорция, члены пропорции, верная и неверная пропорция; сформулировать основное свойство пропорции и научиться применять его для определения верной и неверной пропорции, определять крайние и средние члены пропорции.
Основные понятия и другие компоненты научных знаний по предмету: отношение, пропорция, крайние и средние члены пропорции.
Форма урока: Урок теоретических и практических самостоятельных работ (исследовательского типа).
УМК: Математика. Учебник. 6 класс Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Оборудование: доска, мел, задания на карточках.
ТЕХНОЛОГИЧЕСКАЯ КАРТА
Этап урока
Деятельность учителя
Деятельность ученика
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
Формируемые УУД
1
Организационный момент
Приветствует учеников, контролирует подготовку рабочих мест
Приветствуют учителя, проверяют подготовку рабочих мест
Регулятивные: организация рабочего места, своей деятельности
Личностные: мотивация учения
2
Актуализация знаний, подготовка к введению нового материала
1. Организует фронтальную работу на повторение опорных понятий и вычислений
1. Отвечают на вопросы учителя, выполняют задания
─ Как называется частное двух чисел? (Отношение)
─ Что показывает отношение?
─ Отношение показывает, что число 4(в 3 раза меньше, чем число 12)
─Отношение показывает, что число 15( в 3 раза больше числа 5)
─ Отношение чисел 40 и 10 равно(4 )
─ На клумбе 60 белых и 12 красных роз. Что показывают отношения?
6 : 12, 12 : 6, 6 : 18
Познавательные: структурирование собственных знаний
(Анализ, сравнение)
Коммуникативные: организация и планирование учебного сотрудничества с учителем и одноклассниками
3
Определение темы урока
Выразите отношения в десятичной дроби, процентах и заполните таблицу. = 0,5 = 50% Р = 0,2 = 20% Я = 0,25 = 25% И= 0,75 = 75% П = 0,7 = 70% Ц = 0,6 = 60% О
4
Постановка цели и задач урока
Формулирует тему урока и организует поисковую работу учащихся по постановке задач и плана действий.
Создает эмоциональный настрой на работу.
Формулируют задачи урока и план урока.
Записывают в тетради число и тему урока.
Зная тему урока, попробуйте составить план урока. Что вы должны узнать сегодня на уроке? Что вы хотите узнать? Чему хотите научиться на уроке?
Регулятивные:
Целеполагание
Личностные:
Самоопределение
Коммуникативные:
Умение вступать в диалог, участвовать в коллективном обсуждении вопроса
5
Открытие новых знаний и первичное восприятие нового учебного материала
1. Организует поисковую работу по открытию новых знаний, записывает полученные равенства на доске.
2. Обобщает высказывания обучающихся и вводит понятие пропорции.
Побуждает к высказыванию своего мнения.
3. Вводит понятие крайних и средних членов пропорции.
5. Организует самостоятельную и фронтальную работу обучающихся и акцентирует внимание, что это один из способов определения верной пропорции.
6. Организует самостоятельную работу и самопроверку, оказывает индивидуальную помощь
7. Физкультминутка
8. Побуждает к высказыванию своего мнения, подводит обучающихся к формулировке основного свойства пропорции
9. Организует работу с учебником.
10. Делает вывод о двух способах проверки, и возвращает учащихся к плану урока и поставленным задачам.
1.Определяют признак группировки, составляют равенства, объясняют своё решение.
2. Высказывают свои предположения, озвучивают определение понятия.
3. Работают в парах
4. Находят крайние и средние члены пропорции.
5. Определяют пропорции, из них верные и неверные, аргументируют ответ, объясняют способ определения верной пропорции.
6. Заполняют таблицу, проверяют.
7. Физкультминутка обеспечивает эмоциональную разгрузку обучающихся.
8. Выявляют закономерность, формулируют вывод.
9. Находят в тексте формулировку свойства верной пропорции и обратного утверждения «основного свойства пропорции» и озвучивают
10. Называют второй способ проверки верной пропорции.
1. Найти отношения.
4 : = 8 2,4 : 8 = 0,3 3 : 10 = 0,3
3 : 0,5 = 6 6 : 1 = 6 : = 8
Выпишите равные отношения.
4 : = :
3 : 0,5 = 6 : 1
2,4 : 8 = 3 : 10
2. Какие из пропорций являются верными и неверными?
= верная = верная :16 = : неверная
3 = 3 = ≠ 12
Это первый способ проверки верной пропорции
3. Физкультминутка: «Хлопушка»
Если дробь сократимая, учащиеся — хлопают, если несократимая – то топают.
2/5; 5/7; 8/45; 6/24; 10/25; 3/5; 11/13; 7/14; 6/9; 6/17; 6/8; 12/25.
4. Самостоятельно и индивидуально заполнить таблицу.
b = c : d
=
=
0,02 : 0,04 = 1:2
Крайние члены
Средние члены
Произведение крайних членов
Произведение средних членов
5. Какой вывод можно сделать по результатам выполненной работы?
6. Сформулировать второй способ проверки верной пропорции
Познавательные:
анализ, синтез, сравнение, обобщение, умение осознанно и произвольно строить математическое речевое высказывание в устной форме
Регулятивные:
Коррекция, планирование
Коммуникативные;
Выражение и аргументация своих мыслей с достаточной полнотой и точностью
Личностные: формирование готовности к самообразованию
6
Первичное усвоение нового учебного материала
(применение правил в условиях выполнения учебных заданий)
Организует первичное усвоение основного свойства пропорции в условиях выполнения учебной задачи.
Обеспечивает положительную реакцию учеников на преодоление трудностей.
Выполняют упражнения,
Объясняют полученный результат опираясь на правило.
1. № 760 из учебника
2. № 762 (а,в,д)
Коммуникативные:
учебное сотрудничество с учителем и сверстниками
Регулятивные:
коррекция, оценка,
7
Рефлексия и оценка деятельности
Выявляет качество и уровень усвоения учебного материала, подводит итоги работы класса в целом
Выполняют задания математического диктанта, самооценка перед выполнением работы и после её проверки
Математический диктант
1. Запишите пропорцию: Число 18 так относится к 4, как 27 относится к 6.
2. Запишите пропорцию: Отношение трех к пяти равно отношению двух к семи.
3. Запишите средние члены пропорции: 1
4. Запишите крайние члены пропорции: 2
5. Верна ли пропорция в п.1
6. Верна ли пропорция в п.2
Регулятивные: коррекция, оценка, как осознание того, что уже усвоено, умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы
Личностные: формирование позитивной самооценки
8
Домашнее задание
Дает комментарий к домашнему заданию
Записывают в дневники задание
П.21 выучить правила, №776, 781(а)
Найти информацию, где встречается пропорция в природе.
Рассмотрим то, что математики называют «свойства пропорций». Для начала посмотрим картинку, где свойства пропорций расписаны, как пасхальные яйца.
| Свойства пропорций |
Под первым номером стоит следующее свойство пропорций: произведение крайних членов равно произведению средних. У меня возникает естественный вопрос — это свойство принадлежит равенству, умножению или пропорции? Лично я считаю, что пропорции оказались в этой очереди только потому, что они содержат знак равенства и умножение (оно же деление без фонограммы). Вспомните такое свойство равенства: если левую и правую часть равенства умножить на одно и то же число, равенство не изменится. Берем пропорцию, умножаем, сокращаем, смотрим, что в остатке.
| Свойство равенства |
Как видите, первое свойство пропорций можно получить без всяких перестановок членов пропорции. Да, результат показывает, что произведения крайних и средних членов пропорции равны. Собственно, это и есть математика. Если результат правильный, существует много путей получения такого результата. Достаточно просто воспользоваться математикой. Давайте ещё раз посмотрим на первое свойство пропорций через коэффициент пропорциональности.
| Первое свойство пропорций |
Получилось абсолютное равенство, замаскированное под пропорцию. В противном случае у нас не будет ни равенства, ни пропорции. Только вот произведение состоит не из двух, а из трех сомножителей: числителя, знаменателя и коэффициента пропорциональности. Для превращения этого равенства в пропорцию мы используем переместительные (коммутативные) и сочетательные (ассоциативные) свойства умножения. Вопрос по ходу: коммутативные и ассоциативные свойства математических действий — это разные свойства или одно свойство под разными именами? То, что математики очень любят одно и то же называть разными словами, мы уже знаем. Что бы нас запутать и запутаться самим. Но зато математики знают очень много умных слов. Им есть чему нас, неуков, учить.
Это мы из пропорции получили умножение трех чисел. Теперь попробуем выполнить противоположную процедуру — из умножения трех чисел получим пропорцию. Давайте понаблюдаем за этим «божественным актом сотворения»пропорции.
Берем три числа x, y, z (без всякой задней мысли о неизвестных, просто чтобы с привычными a, b, c, d, k не путать), умножаем их между собой, сравниваем, коммутируем-ассоциируем и создаем пропорции.
| Рождение пропорций |
У нас получились три разные пропорции, созданные из трех разных сомножителей. В качестве коэффициентов пропорциональности в этих пропорциях выступает один из сомножителей. Интересно, эти три пропорции являются близнецами, тройняшками или дальними родственниками? Что-то общее у них должно быть. Например, произведение членов этих трех пропорций (средних или крайних — без разницы) равны между собой. Но это ещё ни о чем не говорит. Существует бесконечное множество других пропорций, произведение членов которых равны произведению членов этой, почти святой, троицы)))
Знают математики о принципах рождения пропорций? Понятия не имею. В учебниках я этого не видел. Возможно, где-то в какой-то диссертации это и описано, но искать крупицу истины в океане математического мусора? Вы меня извините, но пусть математики научатся сами искать то, что умные люди создают. Речь не обо мне. Я говорю о тех многочисленных вещах, которые математики в упор не хотят видеть. Например, вы когда нибудь видели денежные купюры или монеты со знаком минус? И я не видел. А что нам математики рассказывают об отрицательных числах? Что они есть. Выводы делайте сами.
Дальше мы поговорим о втором и третьем свойствах пропорций. А пока, Adele поет песню «Skyfall» без всякой фонограммы.
