Какие свойства у прямоугольника
Прямоугольник, свойства, признаки и формулы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение)
Свойства прямоугольника
Признаки прямоугольника
Формулы прямоугольника
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
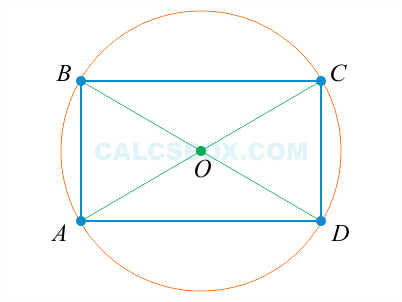
6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Рис. 11. Квадрат
AВ = ВC = AD = CD
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Формула диагонали прямоугольника:
![]() ,
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:
 .
.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
карта сайта
Коэффициент востребованности
1 348
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ), ( angle B = angle D ))
2. Противоположные стороны равны
( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны
( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу
( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны
( AC = BD )

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ).
Следовательно, ( triangle ABD = triangle DCA ) по двум катетам (( AB = CD ) и ( AD ) — совместный).
Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.
Значит, ( AC = BD ).
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
( Rightarrow AB = CD ), ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.
Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ), ( angle B = angle D ).
Выводим, что ( angle A = angle B = angle C = angle D ). Все они по ( 90^{circ} ). В сумме — ( 360^{circ} ).
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
( AC^2=AD^2+CD^2 )
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

8. Точка пересечения диагоналей делит их пополам
( AO = BO = CO = DO )

9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности

10. Сумма всех углов равна 360 градусов
( angle ABC + angle BCD + angle CDA + angle DAB = 360^{circ} )
11. Все углы прямоугольника прямые
( angle ABC = angle BCD = angle CDA = angle DAB = 90^{circ} )

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна ( 180^{circ} )
( angle ABC = angle CDA = 180^{circ},enspace angle BCD = angle DAB = 180^{circ} )
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами.
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб — это параллелограмм, у которого все стороны равны.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.
Вес — это физическая величина, а именно сила, воздействующая на горизонтальную поверхность или вертикальную подвеску.
Азбука Морзе — перечень сигналов из точек и тире, воспроизводящихся с помощью радиосигналов или прерыванием постоянного электрического тока.
Американский нефтяной баррель равен 42 галлонам в английской системе мер или 158,988 л в метрической системе.
Вес одного литра воды примерно 998,5 грамм.
1 чайная ложка, 5 мл жидкости это приблизительно 5 грамм
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
Ïðÿìîóãîëüíèê — ïàðàëëåëîãðàìì ñ ïðÿìûìè óãëàìè, ðàâíûìè 90 ãðàäóñàì è äâóìÿ ïðîòèâîïîëîæíûìè ðàâíûìè ñòîðîíàìè.

 åâêëèäîâîé ãåîìåòðèè äëÿ òîãî, ÷òîáû ÷åòûðåõóãîëüíèê îêàçàëñÿ ïðÿìîóãîëüíèêîì, íóæíî, ÷òîáû õîòÿ áû 3 óãëà áûëè ïðÿìûìè. ×åòâåðòûé óãîë òàêæå áóäåò ðàâåí 90°, èñõîäÿ èç òåîðåìû î ñóììå óãëîâ ìíîãîóãîëüíèêîâ.  íååâêëèäîâîé ãåîìåòðèè, åñëè ñóììà óãëîâ ÷åòûð¸õóãîëüíèêà áîëüøå èëè ìåíüøå 360 ãðàäóñîâ, òàêîé ÷åòûðåõóãîëüíèê íå ìîæåò áûòü ïðÿìîóãîëüíèêîì.
Ðàçíèöà â ïðÿìîóãîëüíèêàõ ëèøü â îòíîøåíèè äëèííîé ñòîðîíû ê êîðîòêîé, â òî âðåìÿ êàê êàæäûé èç ÷åòûðåõ óãëîâ ïðÿìîé (ðàâåí 90°).

Ñâîéñòâà ïðÿìîóãîëüíèêà.
Êðîìå ïàðàëëåëîãðàììà ïðÿìîóãîëüíèêîì ìîãóò áûòü åùå êâàäðàò è ðîìá.
— Ïðÿìîóãîëüíèê — ýòî ïàðàëëåëîãðàìì. Ïðîòèâîëåæàùèå ñòîðîíû ïàðàëëåëüíû äðóã äðóãó.
— Ñòîðîíû ïðÿìîóãîëüíèêà – ýòî åãî æå âûñîòû.
— Êâàäðàò äèàãîíàëè ïðÿìîóãîëüíèêà = ñóììå êâàäðàòîâ 2-õ ñìåæíûõ ñòîðîí (èç òåîðåìû Ïèôàãîðà).
— Âîêðóã âñÿêîãî ïðÿìîóãîëüíèêà ëåãêî îïèñàòü îêðóæíîñòü, ïðè ýòîì äèàãîíàëü ïðÿìîóãîëüíèêà áóäåò ðàâíîé ñ äèàìåòðîì îêðóæíîñòè, êîòîðàÿ îïèñàíà (òîãäà ðàäèóñ îêðóæíîñòè áóäåò ðàâåí ïîëóäèàãîíàëè ïðÿìîóãîëüíèêà).

— Ó ïðîòèâîïîëîæíûõ ñòîðîí ïðÿìîóãîëüíèêà îäèíàêîâàÿ äëèíà, ò.å. ñòîðîíû ðàâíû:
AB = CD, BC = AD
— Ïðîòèâîëåæàùèå ñòîðîíû ïðÿìîóãîëüíèêà ïàðàëëåëüíû äðóã äðóãó:
AB||CD, BC||AD
— Ïðèëåãàþùèå ñòîðîíû ïðÿìîóãîëüíèêà ïåðïåíäèêóëÿðíû:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
— Êàæäûé èõ ÷åòûðåõ óãëîâ ïðÿìîóãîëüíèêà ïðÿìîé:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
— Ñóììà óãëîâ ïðÿìîóãîëüíèêà ñîñòàâëÿåò 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
— Äèàãîíàëè ïðÿìîóãîëüíèêà èìåþò îäèíàêîâûå äëèíû:
AC = BD
— Ñóììà êâàäðàòîâ äèàãîíàëè ïðÿìîóãîëüíèêà ðàâíà ñóììå êâàäðàòîâ ñòîðîí:
2d2 = 2a2 + 2b2
— Âñå äèàãîíàëè ïðÿìîóãîëüíèêà äåëÿò ïðÿìîóãîëüíèê íà 2 îäèíàêîâûå ôèãóðû (åñëè êîíêðåòíåå, íà ïðÿìîóãîëüíûå òðåóãîëüíèêè).
— Äèàãîíàëè ïðÿìîóãîëüíèêà ïåðåñåêàþòñÿ, äåëÿ äðóã äðóãà íà 2 ðàâíûå ÷àñòè:
AO = BO = CO = DO = d/2
— Òî÷êó ïåðåñå÷åíèÿ äèàãîíàëåé íàçûâàþò öåíòðîì ïðÿìîóãîëüíèêà, êðîìå òîãî îíà åñòü öåíòð îïèñàííîé îêðóæíîñòè.
— Äèàãîíàëü ïðÿìîóãîëüíèêà åñòü äèàìåòð îêðóæíîñòè îïèñàííîé.
— Îêîëî ïðÿìîóãîëüíèêà ëåãêî îïèñàòü îêðóæíîñòü, ò.ê. ñóììà ïðîòèâîëåæàùèõ óãëîâ ðàâíà 180°:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
—  ïðÿìîóãîëüíèê ñ íåðàâíîé äëèíîé è øèðèíîé, íèêàê íå âïèñàòü îêðóæíîñòü, ò.ê. ñóììà ïðîòèâîïîëîæíûõ ñòîðîí íå ðàâíà ìåæäó ñîáîé (âïèñàòü îêðóæíîñòü ïîëó÷èòñÿ ëèøü â ÷àñòíûé ñëó÷àé ïðÿìîóãîëüíèêà — êâàäðàò).
Ïëîùàäü ïðÿìîóãîëüíèêà, îíëàéí ðàñ÷åò | |
| Ðàñ÷åò ïëîùàäè ïðÿìîóãîëüíèêà ïî øèðèíå è âûñîòå, äèàãîíàëÿì è óãëó ìåæäó íèìè, êàê íàéòè ïëîùàäü ïðÿìîóãîëüíèêà. | |
| Ïëîùàäü ïðÿìîóãîëüíèêà, îíëàéí ðàñ÷åò | |
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû — ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïàðàëëåëîãðàìì. | |
| Ïàðàëëåëîãðàìì — ýòî ÷åòûðåõóãîëüíèê ñ ïîïàðíî ïàðàëëåëüíûìè ïðîòèâîïîëîæíûìè ñòîðîíàìè (íàõîäÿòñÿ íà ïàðàëëåëüíûõ ïðÿìûõ). | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïàðàëëåëîãðàìì. | |
План-конспект урока (2 класс) учитель начальных классов МОУ СШ № 128 Красильникова Людмила Михайловна
Тема урока: Прямоугольник и его свойства.
Цель: Создать условия для ознакомления учащихся со свойствами прямоугольника и применение знаний на практике.
Организовать исследовательскую деятельность по определению свойств прямоугольника;
Объяснять разницу между двумя прямоугольниками.
Самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве, самостоятельно делать выбор, какой поступок совершить.
Определять цель деятельности на уроке с помощью учителя и самостоятельно; учиться совместно с учителем и формулировать учебную проблему, планировать учебную деятельность на уроке; высказывать свою версию, пытаться предлагать способ её проверки, работая по предложенному плану, использовать необходимые средства (учебник, простейшие приборы и инструменты); определять успешность выполнения своего знания в диалоге с учителем.
ориентироваться в своей системе знаний: понимать, что нужна дополнительная информация (знания), для решения учебной задачи в один шаг; делать предварительный отбор источников информации для решения учебной задачи; добывать новые знания, извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.); перерабатывать полученную информацию: наблюдать и делать самостоятельные выводы.
участвовать в диалоге на уроке; отвечать на вопросы учителя, товарищей по классу;
слушать и понимать речь других; взаимодействовать в паре.
Этап урока | Деятельность учителя | Деятельность учащихся | Методы и формы | Средства | УУД | |||||||||||||||||||||||
I.Самоопре-деление к деятельности (Орг. момент) | Включение в деловой ритм урока Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. — Ребята, сегодня мы с вами постараемся углубить математические знания, узнать что-то новое. Давайте улыбнемся друг другу, пожмем руку и пожелаем удачной работы. Ведь с маленькой удачи начинается большой успех. Итак, в добрый путь. | Приветствуют учителя и друг друга, жмут руку и желают удачной работы. Включаются в деловой ритм урока | Л.. вызвать желание у детей работать, настроить на трудовую деятельность, развитие организационных умений Р. -самостоятельно организовывать свое рабочее место; -планировать учебное сотрудничество с учителем и сверстниками | |||||||||||||||||||||||||
II. Актуализация знаний | На экране и на партах фигуры: —
— Они все одинаковые? — Назовите эти фигуры. — А мы все знаем об этих фигурах? — Какая из этих фигур отличается от других? — Почему? | — Это четырехугольники — Они все разные. 1-ромб 2- прямоугольник 3 – трапеция — Нет. — 2 — у нее прямые углы. | наглядный объяснительно-иллюстративный, фронтальный | презентация | К. -формировать умения слушать и понимать других; -формировать умения строить речевое высказывание в соответствии с поставленными задачами. Р. -формировать умения оценивать учебные действия в соответствии с поставленной задачей. П. -формировать умения на основе анализа рисунка – схемы делать выводы | |||||||||||||||||||||||
III. Мотивационная и целевая установка на урок | Исчезают все фигуры, остается прямоугольник — Какая тема урока? — Какую цель мы поставим на урок? — Какие задачи мы поставим? | Прямоугольник и его свойства. — Узнать, что такое прямоугольник и его свойства. — Распознавать прямоугольник среди других геометрических фигур; — Отличать прямоугольник от других четырехугольников; — Объяснять разницу между прямоугольником и ромбом, прямоугольником и трапецией; — Называть свойства прямоугольника; — Строить прямоугольник на листе; | словесный фронтальный | презентация | Р. -определять цель учебной деятельности с помощью учителя и самостоятельно; -определять план выполнения заданий на уроках, внеурочной деятельности, жизненных ситуациях под руководством учителя. Л. -формировать эмоционального отношения к школе и учебной деятельности. | |||||||||||||||||||||||
IV. Усвоение новых знаний | 1) Вывод определения «прямоугольник» — Рассмотрите прямоугольник.
— К какой группе мы его отнесли? Значит, прямоугольник – это ……четырехугольник. — А чем прямоугольник отличается от остальных фигур в этой группе? — А как определить, что углы прямые? — Так что же такое прямоугольник? | -Четырехугольники — Все углы прямые. — Измерить с помощью угольника. Прямоугольник – это четырехугольник, у которого все углы прямые. | Поисковый Наглядный Фронтальный индивидуальный | Лист деятельности, презентация | П. -формировать умение осуществлять анализ объектов с выделением признаков; — формировать умение выдвижение гипотез и их обоснование; (общеучебные) знаково-символическое моделирование Р. — планировать и прогнозировать; — планировать учебного сотрудничества с учителем и сверстниками -волевая саморегуляция в ситуации затруднения; | |||||||||||||||||||||||
2) Характеристика длины и ширины прямоугольника. — Рассмотрите прямоугольники.
— Сравните стороны, что заметили? — Как можно назвать стороны, которые длиннее? — Как можно назвать стороны, которые короче? | — Одни стороны длиннее, а другие короче. — Такую сторону можно назвать длина. — Такую сторону можно назвать ширина. | исследовательский Наглядный Фронтальный индивидуальный | Лист деятельности, презентация | |||||||||||||||||||||||||
3) Свойства прямоугольника На партах лежат прямоугольники — Посмотрите внимательно на прямоугольник, вглядитесь, может, вы еще что- то интересное заметите у прямоугольника? (Дополнительно: — Обратите внимание на стороны прямоугольника) — А как можно назвать эти стороны, которые находятся напротив друг друга? — Эти стороны, находящиеся напротив друг друга, называются противоположными. (На экране появляется противоположные стороны) — Измерьте стороны прямоугольника, находящиеся друг напротив друга. Сделайте вывод. — Как доказать, что стороны, находящиеся друг напротив друга одинаковые по длине, если нет линейки? — Какой вывод можно сделать? — Дайте определение прямоугольника по его свойствам. | — Стороны, находящиеся друг напротив друга одинаковые по длине. — Они положены друг против друга. Учащиеся измеряют стороны. -Противоположные стороны одинаковые — Проверить сгибанием. Вывод: противоположные стороны равны. Прямоугольник — это четырехугольник, у которого все углы прямые и противоположные стороны равны. | презентация Модели прямоугольников | ||||||||||||||||||||||||||
IV. Первичное закрепление | 1)Распознавание прямоугольников среди других фигур. — Найдите прямоугольники и определите их количество. Проверка!
| Поисковый Наглядный Фронтальный индивидуальный | Лист деятельности, презентация | Р. -формировать умения планировать свою деятельность; -формировать умения контролировать, оценивать и корректировать свои действия. К. -формировать умения строить речевое высказывание в соответствии с поставленными задачами. П. -формировать умения на основе анализа рисунка – схемы делать выводы. -сравнивать и группировать предметы, объекты по нескольким основаниям; находить закономерности; самостоятельно продолжать их по установленном правилу. | ||||||||||||||||||||||||
2 — Рассмотрите чертежи. Выберите те прямоугольники, на которых правильно обозначены длина и ширина
9
3
8 — Данные внесите в таблицу.
— Объясните свой выбор. | — Правильно поставлены измерения у зеленого прямоугольника. — У красной и синей | исследовательский Наглядный Фронтальный групповой | Лист деятельности, презентация | |||||||||||||||||||||||||
3)Распознавание прямоугольников в реальной жизни — Назовите предметы, которые имеют форму прямоугольника
| Поисковый Наглядный Фронтальный индивидуальный | Лист деятельности, презентация | ||||||||||||||||||||||||||
4)Объяснение разницы между прямоугольником и ромбом, прямоугольником и трапецией. — Дайте названия фигурам и сравните их.
И
И
— Какой вывод можно сделать? | Вывод: только у прямоугольника все противоположные стороны равны и все углы прямые | исследовательский Наглядный Фронтальный групповой | Лист деятельности, презентация | |||||||||||||||||||||||||
5) Составление алгоритма построения прямоугольника. — Как мы будем строить прямоугольник? 6) Построение прямоугольника на листе, используя изученные свойства. — Сейчас я предлагаю вам выполнить задание, в котором вы сможете применить новые знания. — Надо достроить треугольник до прямоугольника.
— Какие свойства вы использовали для этого? (Мы знаем, что противоположные стороны прямоугольника равны, поэтому легко смогли достроить фигуру). — Обязательно ли было измерять длины сторон? (Нет) | 1.Поставим точку в угол клеточки. 2.От точки вправо отложим длину, начертим отрезок 3. От точки отложим вниз ширину, начертим ширину. 4.Проведем отрезок второй ширины 5. Проведем отрезок второй длины | исследовательский Наглядный Фронтальный групповой | Лист деятельности, презентация | |||||||||||||||||||||||||
6)С |

 Как называются все эти фигуры?
Как называются все эти фигуры?





 ) Отличие длины и ширины
) Отличие длины и ширины 5
5 4
4





