Какие свойства у параболы
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
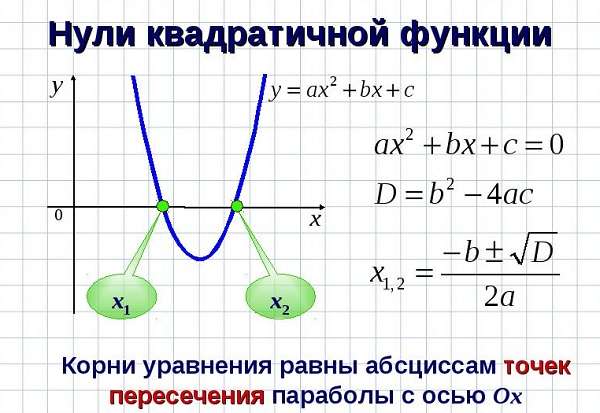
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
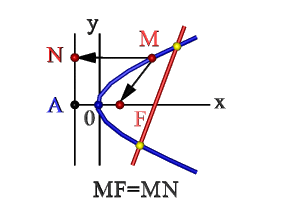
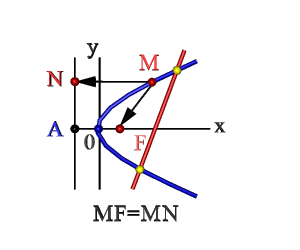
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
y2 = 2 * p * x,
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
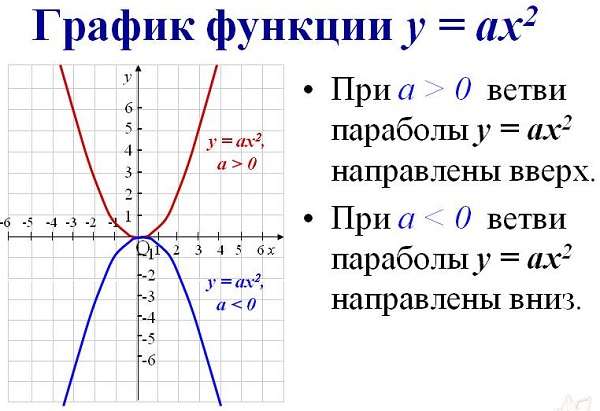
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
- x0 = -b / (2 * a),
- y0 = y (x0).
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
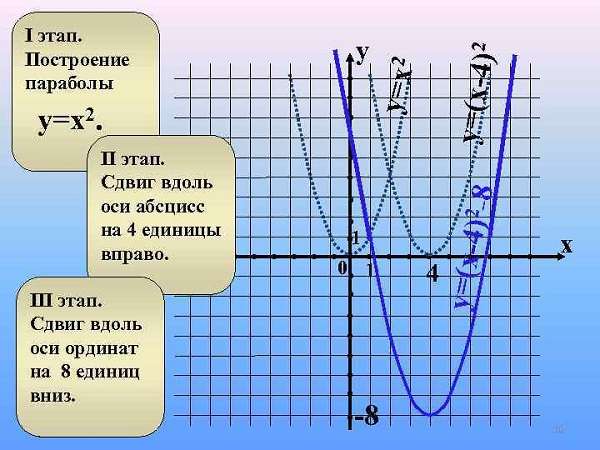
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
D = (b2 4 * a * c).
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Директриса, эксцентриситет, фокус параболы
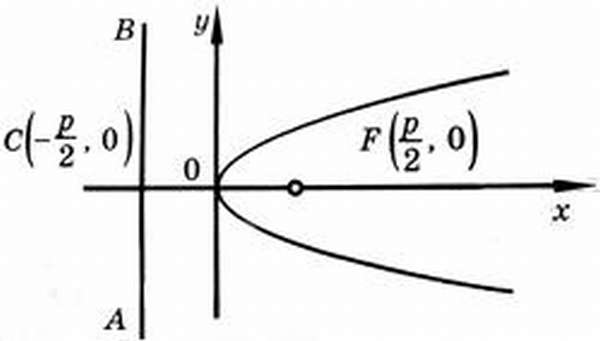
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
График какой из приведенных ниже функций изображен на рисунке?
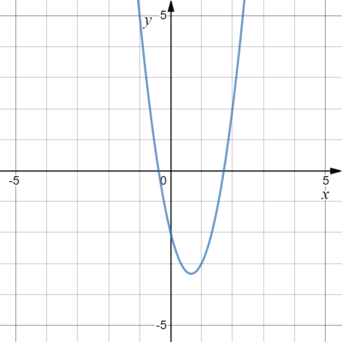
1) (y=-3x^2-4x+2) (;;;) 2)(y=-3x^2-4x-2) (;;;) 3)(y=3x^2-4x+2) (;;;) 4)(y=3x^2-4x-2)
Общее уравнение параболы имеет вид (y=ax^2+bx+c), где знак (a) зависит от направления ветвей параболы, (c) — точка пересечения графика с осью (y).
У данной функции (a>0) — ветви направленны вверх, поэтому варианты 1) и 2) точно не подходят.
Так как график пересекает ось (y) ниже нуля, то (c<0). Подходит вариант 4).
Ответ: 4
На каком рисунке изображен график функции (y=2x^2+5x+1)?
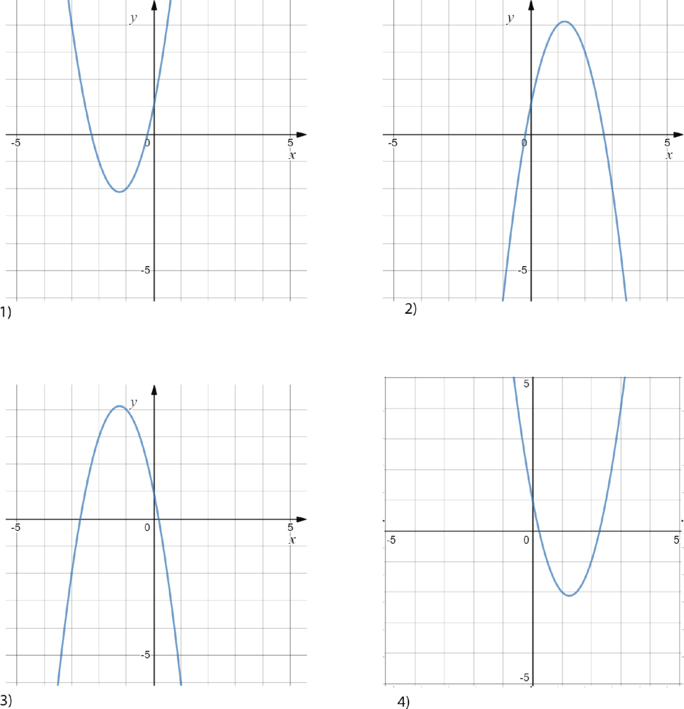
Общее уравнение параболы имеет вид (y=ax^2+bx+c), где знак (a) зависит от направления ветвей параболы, (c) — точка пересечения графика с осью (y).
У данной функции (a>0) — ветви направленны вверх, поэтому варианты 2) и 3) точно не подходят.
Коэффициент (c) у функций 1) и 4) совпадает. Чтобы различить эти функции, используем формулу координаты вершины параболы (x_{text{верш} }= -frac{b}{2a}). По условию, (a=2, b=5), следовательно, (x_{text{верш}}=-frac{5}{4}<0). Подходит вариант 1).
Ответ: 1
Установите соответствие между графиками функций и формулами, которые их задают.
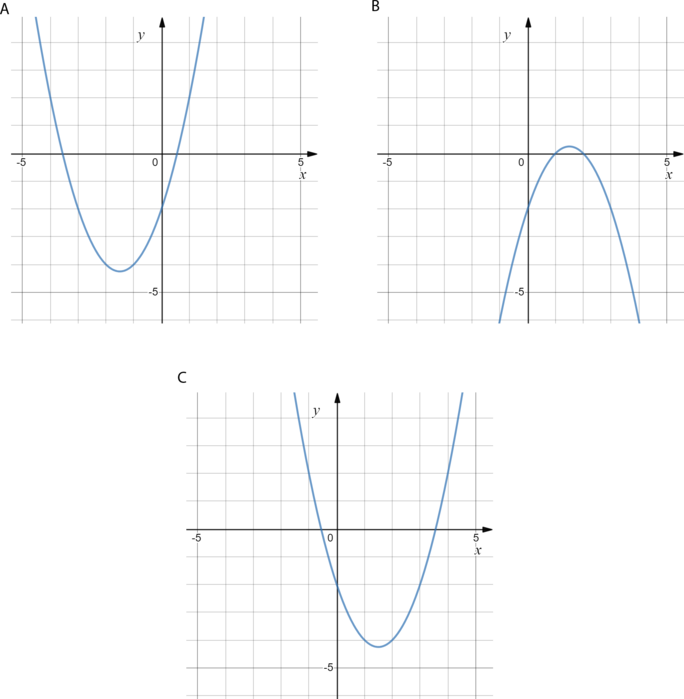
Формулы:
1) (y=x^2+3x-2) (;;;) 2)(y=-x^2+3x-2) (;;;) 3)(y=x^2-3x-2)
В таблице под каждой буквой укажите соответствующий номер.

Общее уравнение параболы имеет вид (y=ax^2+bx+c), где знак (a) зависит от направления ветвей параболы, (c) — точка пересечения графика с осью (y).
Только у графика B ветви направлены вниз, значит, только ему соответствует уравнение, где (a<0), то есть 2).
Рассмотрим графики A и C. Первый из них имеет отрицательную координату (x) вершины параболы, а второй — положительную.
Найдем координату вершины параболы, заданной уравнением 1).
[x_{text{верш} }= -frac{b}{2a}=-frac{3}{2}<0.]
Значит, графику A соответствует формула 1). Графику C соответствует формула 3).
Ответ: 123
Определите значение коэффициента (b) функции (y=ax^2+bx+c) по графику, если известно, что данный график пересекает ось ординат в точке с координатой (0;7).
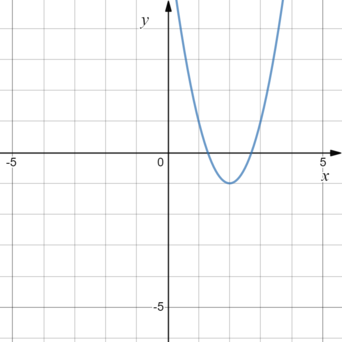
Так как график пересекает ось ординат в точке с координатой (0;7), то коэффициент (c = 7).
Абсцисса вершины параболы (x_{text{верш} }= -frac{b}{2a}=2), значит, (b=-4a).
Ордината вершины параболы (y_{text{верш} }=-1). Но (y_{text{верш} }) можно определить, подставив значение (x=3) с исходное уравнение параболы:
[-1=a cdot 9 — 4a cdot 3 + 7.]
Откуда (a = 2), значит, (b=-4a cdot 2=-8).
Ответ: -8
Определите значение коэффициента (b) функции (y=ax^2+bx+c) по графику.
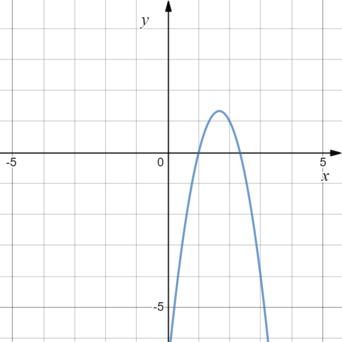
Выберем 3 точки, принадлежащие графику функции, и имеющие целые координаты: (1;0), (2;1) и (3;-4).
Поочередно подставим пары значений ((x;y)) в общее уравнение параболы. Затем решим полученную систему из трех уравнений относительно (a, b, c).
[begin{cases}
0 = a+b+c,\
1 =4a+2b+c,\
-4 =9a+3b+c.
end{cases}]
Выразим (c = -a-b) из первого уравнения и подставим в остальные.
[begin{cases}
1 =4a+2b-a-b, \
-4 =9a+3b-a-b.
end{cases}]
[Rightarrow] [begin{cases}
1 =3a+b,\
-4 =8a+2b.
end{cases}]
Умножим обе части первого уравнения на 2, а затем вычтем полученное уравнение из второго.
[begin{cases}
2 =6a+2b,\
-4 =8a+2b.
end{cases}]
Откуда (-6=2a) или (a=-3). Тогда (b=1-3a=10).
Ответ: 10
График какой из приведенных ниже функций изображен на рисунке?
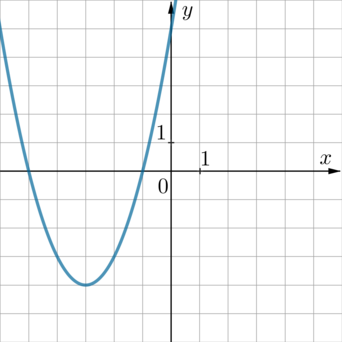
1) (y=-x^2-6x-5qquad) 2) (y=x^2+6x+5qquad ) 3) (y=x^2-6x+5qquad ) 4) (y=-x^2+6x-5)
Способ 1.
Ветви параболы направлены вверх, следовательно, коэффициент перед (x^2) в уравнении параболы положительный. Значит, выбираем между 2 и 3. Вершина параболы на рисунке имеет абсциссу (x_0=-3). У параболы 2 вершина (x_{0_2}=frac{-6}{2cdot 1}=-3), у параболы 3 (x_{0_3}=frac6{2cdot 1}=3). Следовательно, ответ 2.
Способ 2.
Парабола на рисунке пересекает ось (Oy) в точке (y=5) (то есть проходит через точку (x=0, y=5)). Среди данных формул точка (x=0,
y=5) удовлетворяет лишь формулам 2 и 3. Также парабола на рисунке проходит, например, через точку (x=-1, y=0). Среди формул 2 и 3 эта точка удовлетворяет лишь формуле 2.
Ответ: 2
График какой из приведенных ниже функций изображен на рисунке?
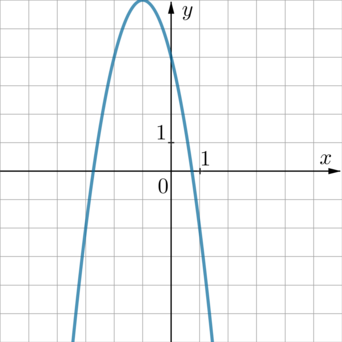
1) (y=-2x^2-4x+4qquad) 2) (y=-2x^2+4x+4qquad ) 3) (y=4x^2-4x-4qquad ) 4) (y=2x^2+4x-4)
Способ 1.
Ветви параболы направлены вниз, следовательно, коэффициент перед (,x^2) в уравнении параболы отрицательный. Значит, выбираем между 1 и 2. Вершина параболы на рисунке имеет абсциссу (x_0=-1). У параболы 1 вершина (x_{0_1}=frac{4}{2cdot (-2)}=-1), у параболы 2 (x_{0_2}=frac{-4}{2cdot (-2)}=1). Следовательно, ответ 1.
Способ 2.
Парабола на рисунке пересекает ось (Oy) в точке (y=4) (то есть проходит через точку (x=0, y=4)). Среди данных формул точка (x=0,
y=4) удовлетворяет лишь формулам 1 и 2. Также парабола на рисунке проходит, например, через точку (x=1, y=-2). Среди формул 1 и 2 эта точка удовлетворяет лишь формуле 1.
Ответ: 1
Парабола
Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.
Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус на оси так, чтобы начало координат помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через расстояние от фокуса к директрисе, тогда у фокуса будут координаты
, .
Для произвольной точки
параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а и поэтому:
Рис. 1
(1)
– каноническое уравнение параболы.
Что такое вершина параболы
Вершина параболы – это парабола, которая проходит через точки
. Если точка принадлежит параболе, то и тоже принадлежит параболе, так как из:.
Значит, парабола симметрична относительно оси
, её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:
Чтобы найти вершину параболы, необходимо знать формулу:
.
Давайте посмотрим, как данная формула действует, допустим дано уравнение:
Тогда:
, , . Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:, , .
Форма и характеристики параболы
Исследуем за каноническим уравнением форму и расположение параболы:
1. В уравнении
переменная входит в парной степени откуда получается, что парабола симметрична относительно оси . Ось – это ось, которая симметрична параболе.
2. Так как
, тогда , откуда получается, что парабола расположена справа от оси .
3. При
мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.
4. При увеличении значений переменной
модуль тоже возрастает. Изобразим параболу на рисунке:
Рис. 2
5. В полярной системе координат, у канонического уравнения параболы такой вид:
6. Уравнение
, , , тоже описывают параболы:
Рис. 3
Оптическое свойство параболы
У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси
. Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.
При положительном
уравнении:
описывают параболу симметричную относительно
с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).
Аналогично изложенному, уравнение
и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .
Примеры решения
Задача
Найти координаты фокуса и составить уравнение директрисы параболы
.
Решение
Сравнивая каноническое уравнение
и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .
Ответ
координаты фокуса:
, а уравнение директрисы параболы: .
Задача
Составить каноническое уравнение параболы:
а) с фокусом в точке
;
б) с фокусом в точке
.
Решение
а). Так как фокус
на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .
б). Фокус
лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .
Ответ
а) каноническое уравнение параболы с фокусом в точке
: ;
б) каноническое уравнение с фокусом в точке
: .
Задача
Показать путём выделения полного квадрата, что уравнение
– это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.
Решение
Выделим относительно переменной
полный квадрат
= = = = = = .
Обозначим
, . Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку , получим каноническое уравнение параболы .
Ветви этой параболы направлены вниз симметрично относительно оси
, , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе .
Повернёмся к старым координатам при помощи замены
, . Уравнение оси в новой системе , а в старой – уравнение оси параболы.
Уравнение директрисы в новой системе координат
, а в старой .
В новой системе
для фокуса , , а в старой системе , , то есть .
Ответ
Каноническое уравнение параболы –
;
вершина – ветви параболы направлены вниз;
, , – фокусное расстояние, а фокус находится в точке ;
уравнение оси
;
уравнение директрисы
.
Ëèíåéíàÿ (ïðÿìîïðîïîðöèîíàëüíàÿ) ôóíêöèÿ.
Îñíîâíîå ñâîéñòâî ëèíåéíûõ ôóíêöèé: ïðèðàùåíèå ôóíêöèè ïðîïîðöèîíàëüíî ïðèðàùåíèþ àðãóìåíòà. Ò.å. ôóíêöèÿ îêàçûâàåòñÿ îáîáùåíèåì ïðÿìîé ïðîïîðöèîíàëüíîñòè.
y = kx + b
Ïðÿìàÿ
Ñòåïåííàÿ ôóíêöèÿ — îáðàòíîïðîïîðöèîíàëüíàÿ — ýòî ôóíêöèîíàëüíàÿ çàâèñèìîñòü, êîãäà óâåëè÷åíèå àðãóìåíòà âûçûâàåò ñîîòâåòñòâóþùåå óìåíüøåíèå ôóíêöèè.
y = k/x
Ãèïåðáîëà
Ôóíêöèÿ Áåññåëÿ ïåðâîãî ðîäà.
Ãðàôèê ôóíêöèè Áåññåëÿ ïîõîæ íà ñèíóñîèäó, êîëåáàíèÿ êîòîðîé çàòóõàþò ïðîïîðöèîíàëüíî , õîòÿ íà ñàìîì äåëå íóëè ôóíêöèè ðàñïîëîæåíû íå ïåðèîäè÷íî.

Ñèíóñîèäà
Êâàäðàòè÷íàÿ ôóíêöèÿ — ïàðàáîëà.
Áîëüøèíñòâî ñâîéñòâ êâàäðàòè÷íîé ôóíêöèè ñâÿçàíû ñ çíà÷åíèåì äèñêðèìèíàíòà.
y = x2

Ïàðàáîëà
Êâàäðàòè÷íàÿ ôóíêöèÿ.
Îáùèé ñëó÷àé êâàäðàòè÷íîé çàâèñèìîñòè: êîýôôèöèåíò a — ïðîèçâîëüíîå äåéñòâèòåëüíîå ÷èñëî íå ðàâíîå íóëþ (a ïðèíàäëåæèò R, a ≠ 0), b, c — ëþáûå äåéñòâèòåëüíûå ÷èñëà.
y = ax2 + bx + c

Ïàðàáîëà
Ñòåïåííàÿ ôóíêöèÿ — ýòî ôóíêöèÿ y = xa, ãäå a — íåêîòîðîå âåùåñòâåííîå ÷èñëî. Ê ñòåïåííûì ÷àñòî îòíîñÿò è ôóíêöèþ âèäà y = kxa, ãäå k — íåêîòîðûé (íåíóëåâîé) êîýôôèöèåíò.
y = x3

Êóáè÷åñêàÿ ïàðàáîëà
Ñòåïåííàÿ ôóíêöèÿ — êîðåíü êâàäðàòíûé.
Ñàìûé ïðîñòîé ñëó÷àé äëÿ äðîáíîé ñòåïåíè (x1/2 = √x).
y = x1/2

Ãðàôèê ôóíêöèè
y = √x
Ñòåïåííàÿ — îáðàòíàÿ ïðîïîðöèîíàëüíîñòü.
Ñàìûé ïðîñòîé ñëó÷àé äëÿ öåëîé îòðèöàòåëüíîé ñòåïåíè (1/x = x-1) — îáðàòíî-ïðîïîðöèîíàëüíàÿ çàâèñèìîñòü. Çäåñü k = 1.
y = k/x

Ãèïåðáîëà
Ïîêàçàòåëüíàÿ ôóíêöèÿ — ìàòåìàòè÷åñêàÿ ôóíêöèÿ f (x) = ax, ãäå a íàçûâàåòñÿ îñíîâàíèåì ñòåïåíè, à x — ïîêàçàòåëåì ñòåïåíè.
y = ex

Ýêñïîíåíòà
Ïîêàçàòåëüíàÿ ôóíêöèÿ.
Ïîêàçàòåëüíàÿ ôóíêöèÿ îïðåäåëåíà äëÿ a > 0 è a ≠ 1. Ãðàôèêè ôóíêöèè ñóùåñòâåííî çàâèñÿò îò çíà÷åíèÿ ïàðàìåòðà a. Çäåñü ïðèìåð äëÿ y = 2x (a = 2 > 1).
y = ax

Ãðàôèê ïîêàçàòåëüíîé ôóíêöèè à>1
Ïîêàçàòåëüíàÿ ôóíêöèÿ.
Ïîêàçàòåëüíàÿ ôóíêöèÿ îïðåäåëåíà äëÿ a > 0 è a ≠ 1. Ãðàôèêè ôóíêöèè ñóùåñòâåííî çàâèñÿò îò çíà÷åíèÿ ïàðàìåòðà a. Çäåñü ïðèìåð äëÿ y = 0,5x (a = 1/2 < 1).
y = ax

Ãðàôèê ïîêàçàòåëüíîé ôóíêöèè 0
Ëîãàðèôìè÷åñêàÿ ôóíêöèÿ.
Ãðàôèê ëþáîé ëîãàðèôìè÷åñêîé ôóíêöèè ïðîõîäèò ÷åðåç òî÷êó (1;0).
y = ln(x)

Íàòóðàëüíûé ëîãàðèôì
Ëîãàðèôìè÷åñêàÿ ôóíêöèÿ.
Ëîãàðèôìû îïðåäåëåíû äëÿ a > 0 è a ≠ 1. Ãðàôèêè ôóíêöèè ñèëüíî ñâÿçàíû ñî çíà÷åíèåì ïàðàìåòðà a. Çäåñü ïðèìåð äëÿ y = log2x (a = 2 > 1).
y = logax

Ãðàôèê ëîãàðèôìè÷åñêîé ôóíêöèè — ëîãàðèôì ïî îñíîâàíèþ à>1
Ñèíóñ.
Ñèíóñîèäà — ïåðèîäè÷åñêàÿ ôóíêöèÿ ñ ïåðèîäîì Ò = 2π
y = sinx
Ñèíóñîèäà
Êîñèíóñ.
Òðèãîíîìåòðè÷åñêàÿ ôóíêöèÿ êîñèíóñ. Ãðàôèêè ó = sinx è ó = cosx ñäâèíóòû ïî îñè õ íà .
y = cosx
Êîñèíóñîèäà
Òàíãåíñ.
Òðèãîíîìåòðè÷åñêàÿ ôóíêöèÿ òàíãåíñ. Òî÷êè ðàçðûâà ïðè õ = (2k -1), ãäå k = 0, ±1, ±2,.. Âåðòèêàëüíûå àñèìïòîòû â ýòèõ òî÷êàõ.
y = tgx
Òàíãåíñîèäà
Ãèïåðáîëè÷åñêèé ñèíóñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

Ýêñïîíåíòà
Ãèïåðáîëè÷åñêèé êîñèíóñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

Ïàðàáîëà
Ãèïåðáîëè÷åñêèé òàíãåíñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

Òàíãåíñîèäà
Ãèïåðáîëè÷åñêèé êîòàíãåíñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

Ãèïåðáîëà
Ãèïåðáîëè÷åñêèé ñåêàíñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

Ãèïåðáîëè÷åñêèé êîñåêàíñ — ýòî ýëåìåíòàðíàÿ ôóíêöèÿ, âûðàæàþùàÿñÿ ÷åðåç ýêñïîíåíòó è òåñíî ñâÿçàííàÿ ñ åå òðèãîíîìåòðè÷åñêèìè ôóíêöèÿìè.

