Какие свойства у овала
Виктор Чебыкин
Введение
Продолжая рассмотрение эллипсовидных овальных кривых (Э.О.К.), начатое в статьях [1], [2] и [3], остановимся еще на трех: циклоидальный овал; гиперэллипс Ламе; овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1). При этом также попробуем классифицировать их и другие Э.О.К. на три группы: гиперовалы, гипоовалы и гипергипоовалы. В последнем разделе речь идет об идентификации Э.О.К.
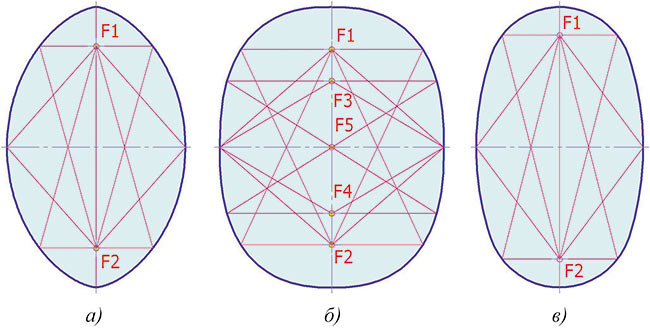
Рис. 1. Овальные кривые: а — циклоидальный овал; б — гиперэллипс Ламе;
в — овальная кривая Rr (гиперовал)
Циклоидальный овал
Циклоидальный овал (рис. 1а и 2) — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая, полученная в результате зеркальной стыковки двух «арок» циклоиды. Циклоида — плоская трансцендентная кривая; это траектория точки окружности, катящейся по прямой линии [4].
Одним из свойств циклоидального овала является наличие двух фокусов, имеющих строго определенное расположение.
Фокусы могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. Это свойство совпадает с аналогичным у кривой R1, описанной в [3]. Точки падения этих лучей на кривую, так же как у кривой R1, являются характерными — в них меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный.
Еще одно свойство циклоидального овала: размеры некоторых элементов овала могут быть вычислены как произведение радиуса производящей окружности данной циклоиды или размеров полуосей с определенными константами. О последних и пойдет речь далее.

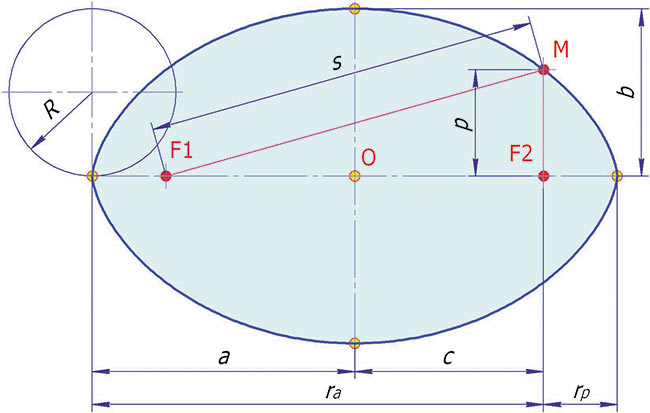
Рис. 2. Циклоидальный овал
Элементы овала (рис. 2):
- R — радиус производящей окружности циклоиды;
- a — большая полуось;
- b — малая полуось;
- с — фокальный радиус (полурасстояние между фокусами);
- p — малый фокальный луч;
- s — большой фокальный луч;
- rp — перифокусное расстояние (минимальное расстояние от фокуса до точки на овале);
- ra — апофокусное расстояние (максимальное расстояние от фокуса до точки на овале).
Константы циклоидального овала:
- Константа соотношения осей овала
Ксо1 = а/b = p/2; - Фокальная константа
Vco = c/R ≈ 2,259 360 664 54…; - Перифокусная константа
PVco = rp/R ≈ 0,882 231 989 04…; - Апофокусная константа
AVco = ra/R ≈ 5,400 953 318 13…; - Эксцентриситетконстанта
Eco = с/a ≈ 0,719 176 835 98…; - Константа малого фокального луча
Lco = p/R ≈ 1,270 684 347 65…; - Константа большого фокального луча
GLco = s/R ≈ 4,693 983 506 71…
Попытка найти в литературе и Интернете сведения по константам циклоидальных овалов ничем не увенчалась, поэтому названия констант и их обозначения автор предложил свои. Ну и значения констант, за исключением первой, пришлось определить самому.
Теперь отнесем этот овал к одной из групп: гиперовалы (от греч., гипер — «над, выше»); гипоовалы (гипо — «под, ниже»); гипергипоовалы.
Построим по полюсам данного овала эллипс и увидим, что он будет описанным по отношению к овалу, а овал соответственно — вписанным в эллипс. Исходя из этого, циклоидальный овал является гипоовалом. Циклоидальные кривые используются в технике: маятник Гюйгенса; кривая кратчайшего спуска; циклоидальные передачи и редукторы; кулачки и эксцентрики…
Гиперэллипс Ламе
Кривая показана на рис. 1б. Такую форму и такое название кривая имеет, если степени m и n в формуле кривой Ламе больше 2.
Гиперэллипс, так же, как овал Кассини (который описан в [3]), имеет два основных оптических фокуса и три дополнительных. Само название его говорит о том, к какой группе следует отнести этот овал — к гиперовалам.

Рис. 3. Разновидности овальных кривых Rr
Гипоэллипс Ламе, показанный в [3], где он был назван просто кривой Ламе, в формуле имеет степени m и n меньше 2. При степенях m и n равных 2 кривая Ламе является эллипсом. В случае если одна из степеней больше, а другая меньше 2, мы имеем гипергипоэллипс (рисунок не показан). Если по полюсам этого овала построить эллипс, то можно увидеть, что кривые имеют как точки касания, так и точки пересечения между собой.
Овальная кривая Rr
Овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1в и 3). Эти овалы хорошо известны тем, кто учился в докомпьютерную эру (по аналогии с «до н.э.» имеем «до к.э.»). Ими пользовались для упрощенного изображения эллипсов на чертежах. Сейчас, по понятным причинам, необходимость в этом отпала. В технике эти овалы все же используются — кулачки, эксцентрики и т.п.
На рис. 1в изображена овальная кривая Rr (гиперовал), а на рис. 3 —сразу три вида овалов: внутренний — гиперовал; наружный — гипоовал; средний — гипергипоовал. Тонкими линиями показаны соответствующие этим овалам эллипсы, которые помогают определить принадлежность кривых к той или иной группе.
Классификация кривых, описанных в статье [3]:
- овал Кассини — гиперовал;
- кривая Ламе (показанная) — гипоовал;
- кривые R0 и R1 — гипоовалы;
- кривая R2: верхняя часть — гиперовал, нижняя — гипоовал.
Идентификация эллипсовидных овальных кривых
Итак, для идентификации предлагаются следующие кривые: эллипс, овал Кассини, гиперэллипс Ламе; гипоэллипс Ламе; гипергипоэллипс Ламе; овал R0; овал R1; циклоидальный овал; гиперовал Rr; гипоовал Rr; гипергипоовал Rr. Зная геометрию и свойства данных кривых, классификацию можно выполнить визуально, однако иногда некоторые из них бывают очень схожи.
Идентификацию лучше проводить в той CADпрограмме, в которой эти кривые созданы. Автор для построения и идентификации кривых использовал программу КОМПАС.
При поочередном входе в режим редактирования кривых можно сразу распознать эллипс и все овалы по сопрягаемым дугам окружностей, группу которых определяем сопряжением с эллипсом. Все остальные кривые при редактировании покажут, что построены с помощью кривой Безье.
Оставшиеся кривые сначала необходимо разбить на группы в соответствии с нашей классификацией путем сопряжения с соответствующими им эллипсами.
В группе гипергипоовалов окажется только гипергипоэллипс, так как гипергипоовал Rr распознан уже на первой стадии идентификации.
Далее рассмотрим группу гипоовалов. Поскольку гипоовал Rr также распознан на первой стадии, в ней остаются: кривая R0; кривая R1; гипоэллипс Ламе; циклоидальный овал. Последний распознаем с помощью эксцентриситетконстанты циклоидального овала (пригодилась!). Для этого поочередно для каждой кривой рассчитываем фокальный радиус, умножая размер большой полуоси на эксцентриситетконстанту Eco. Тот овал, в котором пучок из восьми лучей, выпущенных из фокуса и отраженных от кривой, соберется в противоположном фокусе, и будет циклоидальным овалом. Для распознавания оставшихся трех гипоовалов рассмотрим три возможных сценария идентификации. Все зависит от количества фокусов у гипоэллипса Ламе. Первый вариант — кривая Ламе имеет четыре фокуса (например, при сочетании параметров: a/b = 7/10; n = m = 1,7). В этом случае удается распознать все кривые: бесфокусную R0, двухфокусную R1 и четырехфокусную кривую Ламе. Второй вариант — кривая Ламе бесфокусная (например, при сочетании параметров: a/b = 8/10; n = m = 1,7). При этом сможем распознать только R1. Кривая R0 и гипоэллипс будут трудноразличимыми. Третий вариант — кривая Ламе имеет два фокуса (например, при сочетании параметров: a/b = 8/10; n = 1,7 и m=1,9). Выявить при этом удастся только кривую R0. Различить R1 и гипоэллипс Ламе можно по форме кривых и расположению фокусов…
Осталось разобраться с гиперовалами. После первой стадии идентификации, где был определен гиперовал Rr, их у нас осталось два: овал Кассини и гиперэллипс Ламе. Для идентификации их в первую очередь необходимо выровнять масштабированием размеров овалов по высоте. Далее нужно определить положение фокусов (тех, которые фигурируют в определении овала Кассини) относительно центра и нанести их. Оптические фокусы овалов использовать нельзя — у них другие координаты. Та кривая, на которой будет соблюдено следующее условие: произведение расстояний от любой точки кривой до фокусов есть величина постоянная, — и есть овал Кассини. Если степени гиперэллипса Ламе равны 2,5 и более, то кривые хорошо различимы визуально — кривая Ламе более угловатая.
Выводов делать не будем. Главное, что почти все точки над «о» расставлены.
Библиографический список
- Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы. Справочник // Инженерный журнал. 2012. № 11. С. 3133.
- Чебыкин В.Г. Особенности технологии врезки люков и патрубков в обечайки резервуаров // Технология машиностроения. 2013. № 1. С. 3335.
- Чебыкин В. А не замахнуться ли нам на Габриеля нашего Ламе? // САПР и графика. 2013. № 8. С. 92, 9495.
- Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982. Т.5. С. 809.
Нижние индексы «co» означают циклоидальный овал (cycloidal oval).
САПР и графика 3`2014
В школе большинству из нас не раз объясняли, в чём отличие радиуса от диаметра, серной кислоты от соляной, эллипса от овала. Но прошли годы, и школьные знания, «слежавшись» под весом многолетней будничной рутины, по большей части позабылись. В рамках данной статьи мы попытаемся восполнить хотя бы один досадный пробел в знаниях и подробнее рассмотрим последний из приведённых примеров, научившись отличать овал от эллипса. Для начала обозначим ключевые определения.
Овал
Под овалом в геометрии понимается вытянутая замкнутая фигура правильной формы. Овал относится к двухмерным фигурам и обладает особыми свойствами. Само слово образовано от французского Ovale, которое, в свою очередь, имеет общие корни с латинской лексемой ovum, что в переводе означает «яйцо». Кривая этого геометрического объекта имеет с любой прямой не более двух общих точек.
Справка! Нельзя сказать, что человек, называющий данную геометрическую фигуру просто «кругом», абсолютно прав. На самом деле окружность (в которой, как мы знаем, все точки кривой равноудалены от центра) – это одна из множества вариаций овала.
Существует структурно более сложное понятие овала в инженерной графике. В этой отрасли науки данным термином обозначают фигуру, имеющую две оси симметрии и построенную при помощи сочетания четырёх участков кривых линий от двух радиусов. Эти участки подобраны таким образом, чтобы обеспечить «перетекание» от одного радиуса к другому без нарушения симметрии и контура фигуры. Если определять координаты точки, постоянно движущейся по линии овала, то она всегда будет находиться на одном из вышеописанных радиусов кривизны. Эти радиусы считаются «фиксированными».
Эллипс
У слова «эллипс» имеются греческие корни, наиболее близкие по переводу к словам «нехватка, недостаток, опущение». Чего же не хватает в эллипсе и что эта фигура вообще из себя представляет?
Эллипсом принято считать любую замкнутую кривую на плоскости, которая имеет четыре вершины в так называемых точках экстремума. Точки фокуса эллипса равноудалены от его вершин. Стороны эллипса будут симметричны, если разделить его в любом направлении прямой, проходящей через его центр. Впрочем, это правило действительно и для фигур овального типа.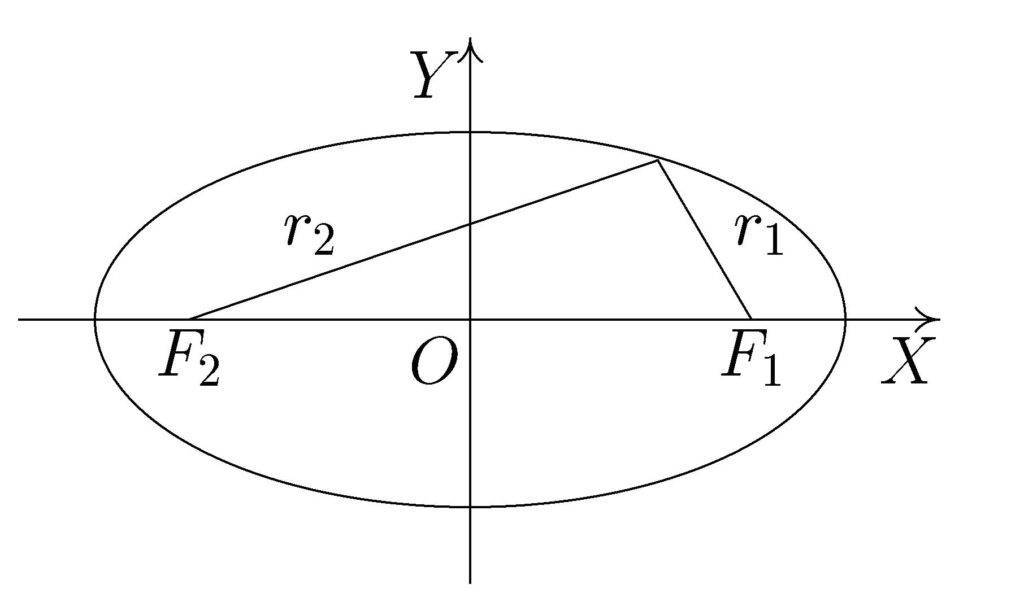
Что общего
Рассматривая вопрос о том, что может быть общего между овальной и эллиптической фигурой, можно заключить, что они имеют весьма похожий внешний вид. Кроме того, обе фигуры располагаются в так называемом евклидовом пространстве. На простом языке евклидово пространство можно объяснить как двумерное пространство, в котором положение точки может быть обозначено при помощи двух чисел, обозначающей её координаты.
В чём отличие эллипса от овала
Различия между двумя этими весьма смежными понятиями вытекают в основном из их определений. Вернувшись к рассмотренному нами определению овала в инженерной графике, можно заключить, что он, в отличие от эллипса, в котором радиус кривизны варьируется перманентно, обладает «фиксированными» радиусами.
Справка! В трёхмерном пространстве возможно построение объёмного овала. Такие фигуры называются эллипсоидами и способны иметь приплюснутую или вытянутую форму. Эта форма достаточно широко распространена в макромире: ею обладает огромное количество известных планет и даже галактики.
Для овальных фигур существует великое множество вариантов построения. Оси их, начинающиеся в точках своих вершин, имеют различные соотношения между собой. В случае же с эллиптическими фигурами в силу вступают особые правила построения. Говоря проще, овалом обозначают более общее понятие, а эллипсом – лишь одно из его проявлений.
( 2 оценки, среднее 4.5 из 5 )
Александр Титов
Просветленный
(41387)
4 года назад
Овал — замкнутая кривая, очерченная дугами окружностей, плавно переходящих друг в друга.
Эллипс — кривая, состоящая из всех точек, сумма расстояний от которых до двух заданных точек есть величина постоянная.
Эллипс можно рассматривать как проекцию окружности на плоскость, пересекающую плоскость окружности под острым углом или как сечение прямого кругового цилиндра плоскостью, пересекающую ось цилиндра под острым углом.
Овал состоит из четырёх дуг окружностей. Эллипс не состоит из дуг окружностей.
На рисунке слева показан овал. Разными цветами выделены дуги окружностей разного радиуса. Точка, в которой одна дуга переходит в другую, есть точка сопряжения, в ней можно провести касательную к обеим дугам. С математической точки зрения это означает, что функция, соответствующая, например, верхней половине овала будет дифференцируемой в точках сопряжения.
Эллипс есть аксонометрическая проекция окружности — при построении трёхмерных объектов окружности правильно изображать в виде эллипсов. Но поскольку эллипс построить точно невозможно (можно лишь построить сколько угодно точек, принадлежащих эллипсу), то вместо эллипсов для изображения окружностей часто используют овалы.
В бытовой речи овалом называется округленная сплюснутая или вытянутая фигура, в т. ч. и эллипс.
Тритон Алексеевич
Мастер
(1552)
4 года назад
овал это немного растянут круг, а эллипс это фигура начертена 2 расстоянием между двона точками.. если привезать нитку двум гвоздям, то натягнуть карандашом нитку по кругу вести, получится эллипс…
Roman Petrov
Мудрец
(18216)
4 года назад
Эллипс — математический объект, замкнутая кривая, описываемая каноническим уравнением:
x^2/a^2+y^2/b^2=1, где
a и b — полуоси.
А овал — это произвольно сплюснутая/вытянутая окружность.
(В общем случае — замкнутая выпуклая плоская кривая).
Любой эллипс является овалом, не каждый овал — эллипсом.
Источник: вики
Гек Финн
Мастер
(2350)
2 года назад
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.
Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.
Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.
Отличие овала от эллипса
1. Объём. Овал – более широкое понятие, в объём которого входит эллипс.
2. Свойства. У эллипса сумма расстояний от двух фокусов, лежащих на большой оси, до точки на кривой, является одинаковым и равно длине центральной оси.
Суперэллипс при n = 1/2, a = b = 1
Суперэллипс при n = 3/2, a = b = 1
Сквиркл, суперэллипс при n = 4, a = b = 1
Суперэллипс (кривая Ламе) — геометрическая кривая, задаваемая в декартовых координатах уравнением
где n, a и b — положительные числа.
Формула задаёт замкнутую кривую, ограниченную прямоугольником −a ≤ x ≤ +a и −b ≤ y ≤ +b. Параметры a и b называются полуосями или полудиаметрами кривой.
Когда n заключено между 0 и 1, суперэллипс выглядит как четырёхконечная звезда с вогнутыми сторонами. В частности, при n = 1/2 стороны звезды являются параболами.
Когда n = 1, кривая представляет собой ромб с вершинами (±a, 0) и (0, ±b). При n в промежутке от 1 до 2 кривая выглядит как ромб с выпуклыми сторонами.
При n = 2 кривая превращается в эллипс (в частности, при a = b — в окружность). При n > 2, кривая выглядит как прямоугольник со скруглёнными углами. В точках (±a, 0) and (0, ±b) кривизна кривой равна нулю.
При n < 2 кривая иногда называется «гипоэллипсом», а при n > 2 — «гиперэллипсом».
Экстремальные точки суперэллипса равны (±a, 0) и (0, ±b), а координаты «углов» (то есть точек пересечения с диагоналями описанного прямоугольника) — (±sa, ±sb), где [1]).
Алгебраические свойства[править | править код]
Когда n представляет собой ненулевое рациональное число p/q, суперэллипс представляет собой алгебраическую кривую. Для положительных n порядок равен pq, для отрицательных — 2pq. В частности, когда a = b = 1 и n чётное целое, суперэллипс представляет собой кривую Ферма степени n. В этом случае она не является сингулярной, хотя в общем случае сингулярна (англ.)русск..
Анимация: суперэллипсы при различных n
Например, если x4/3 + y4/3 = 1, то кривая является алгебраической кривой степени 12 третьего рода, задаваемая неявным уравнением
или параметрическим уравнением
или
Площадь суперэллипса выражается формулой
Обобщения[править | править код]
Пример обобщённого суперэллипса с m ≠ n
Суперэллипс можно обобщить в виде:
или
(здесь — параметр, который не следует интерпретировать как угол).
История[править | править код]
Суперэллипс в виде уравнения в декартовых координатах как обобщение обычного эллипса впервые предложил Габриель Ламе (1795—1870).
Иногда «изобретение» суперэллипса ошибочно приписывают датскому поэту и учёному Питу Хейну (1905—1996). В 1959 году архитектурное управление Стокгольма объявила конкурс на проектирование круговой развязки вокруг площади Сергельсторг. Пит Хейн стал победителем конкурса, предложив транспортное кольцо в виде суперэллипса с n = 2,5 и a/b = 6/5[2]. Реконструкция площади была завершена в 1967 году. Хейн использовал суперэллипс в других дизайнерских разработках — кроватях, тарелках, столах[3]. Вращая суперэллипс вокруг длинной оси, он получил «суперъяйцо», которое стало популярной игрушкой, поскольку в отличие от обычного яйца могло стоять на плоской поверхности.
В 1968 году, когда делегации на переговорах в Париже по вьетнамской войне не могли прийти к согласию о форме стола, был предложен стол в виде суперэллипса[2]. Суперэллиптическую форму имеет стадион «Ацтека» в Мехико, главный стадион Олимпийских игр 1968 года.
Валдо Тоблер в 1973 году разработал картографическую проекцию, известную как гиперэллиптическая проекция Тоблера, в которой меридианы представляют собой суперэллипсы[4].
Шрифт Melior, созданный Германом Цапфом в 1952 году имеет суперэллиптические буквы «o». Считается, что Цапф выбрал форму буквы интуитивно, не имея понятия о математическом содержании этой формы, и только позже Пит Хейн отметил сходство элементов некоторых букв шрифта с суперэллипсами. 30 лет спустя Дональд Кнут встроил в семейство своих шрифтов Computer Modern возможность выбора между настоящими эллипсами и суперэллипсами (обе формы апроксимировались кубическими сплайнами).
На логотипе футбольной команды «Питсбург Стилерз» изображены три четырёхугольных звезды, которые представляют собой суперэллипсы с n = 0,5.
См. также[править | править код]
- Астроида — суперэллипс с n = 2/3 и a = b, гипоциклоида с четырьмя углами.
- Дельтоида — трёхугольная гипоциклоида.
- Сквиркл — суперэллипс n = 4 и a = b, выглядящий как «четырёхугольное колесо».
- Треугольник Рёло — «трёхугольное колесо».
- Суперформула — обобщение суперэллипса.
- Суперквадрики — трёхмерные аналоги суперэллипсов.
Примечания[править | править код]
- ↑ Donald Knuth: The METAFONTbook, p. 126
- ↑ 1 2 Gardner, Martin (1977), Piet Hein’s Superellipse, Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American, New York: Vintage Press, с. 240–254, ISBN 978-0-394-72349-5
- ↑ The Superellipse, in The Guide to Life, The Universe and Everything by BBC (27th June 2003)
- ↑ Tobler, Waldo (1973), The hyperelliptical and other new pseudocylindrical equal area map projections, Journal of Geophysical Research Т. 78 (11): 1753–1759, DOI 10.1029/JB078i011p01753
Ссылки[править | править код]
- Barr, Alan H. (1983), Geometric Modeling and Fluid Dynamic Analysis of Swimming Spermatozoa, Rensselaer Polytechnic Institute (Ph.D. dissertation using superellipsoids)
- Barr, Alan H. (1992), Rigid Physically Based Superquadrics, in Kirk, David, Graphics Gems III, Academic Press, с. 137–159 (code: 472–477), ISBN 978-0-12-409672-1
- Gielis, Johan (2003), Inventing the Circle: The Geometry of Nature, Antwerp: Geniaal Press, ISBN 978-90-807756-1-9
- Sokolov, D. D. (2001), Lamé curve, Springer Encyclopaedia of Mathematics, <https://eom.springer.de/L/l057390.htm>
- Superellipse Calculator & Template Generator
- Superellipse (MathWorld)
- Johan Gielis’ and Bert Beirinckx’ «Superformula».
