Какие свойства света подтверждают эффект комптона
Фотон и его свойства | |
Фотон — материальная, электрически нейтральная частица, квант электромагнитного поля (переносчик электромагнитного взаимодействия). | |
Основные свойства фотона
| |
Энергия фотона:. Согласно теории относительности энергия всегда может быть вычислена как , Отсюда — масса фотона. Импульс фотона . Импульс фотона направлен по световому пучку. | |
Наличие импульса подтверждается экспериментально: существованием светового давления. | |
Давление света | |
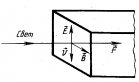
В 1873 г. Дж. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствие(благодаря действию силы Лоренца; на рисунке v — направление скорости электронов под действием электрической составляющей электромагнитной волны). |
|
Квантовая теория света объясняет световое давление как результат передачи фотонами своего импульса атомам или молекулам вещества. Пусть на поверхность абсолютно черного тела площадью S перпендикулярно к ней ежесекундно падает N фотонов: . Каждый фотон обладает импульсом . Полный импульс, получаемый поверхностью тела, равен . Световое давление: | |
При падении света на зеркальную поверхность удар фотона считают абсолютно упругим, поэтому изменение импульса и давление в 2 раза больше, чем при падении на черную поверхность (удар неупругий). |
|
Это давление оказалось ~4.10-6 Па. Предсказание Дж. Максвеллом существования светового давления было экспериментально подтверждено П. Н.Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Теория и эксперимент совпали. Опыты П. Н. Лебедева — экспериментальное доказательство факта: фотоны обладают импульсом | |
Эффект Комптона (1923) | |
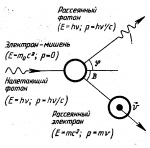
А. Комптон на опыте подтвердил квантовую теорию света. С точки зрения волновой теории световые волны должны рассеиваться на малых частицах без какого-либо изменения частоты излучения, что опытом не подтверждается. При исследовании законов рассеяния рентгеновских лучей А. Комптон установил, что при прохождении рентгеновских лучей через вещество происходит увеличение длины волны рассеянного излучения по сравнению с длиной волны падающего излучения. Чем больше угол рассеяния, тем больше потери энергии, а следовательно, и уменьшение частоты (увеличение длины волны). Если считать, что пучок рентгеновских лучей состоит из фотонов, которые летят со скоростью света, то результаты опытов А. Комптона можно объяснить следующим образом. Законы сохранения энергии и импульса для системы фотон — электрон: |
|
где m0c2 — энергия неподвижного электрона; hv — энергия фотона до столкновения; hv‘ — энергия фотона после столкноВЕНИЯ, P и p’ — импульсы фотона до и после столкновения; mv — импульс электрона после столкновения с фотоном. | |
Решение системы уравнений для энергии и импульса с учетом того, что дает формулу для измерения длины волны при рассеянии фотона на (неподвижных) электронах: | |
где — так называемая комптоновская длина волны. | |
Корпускулярно-волновой дуализм | |
Конец XIX в.: фотоэффект и эффект Комптона подтвердили теорию Ньютона, а явления дифракции, интерференции света подтвердили теорию Гюйгенса. | |
Таким образом, многие физики в начале XX в. пришли к выводу, что свет обладает двумя свойствами: | |
| |
Чем больше v, тем ярче выражены квантовые свойства света и менее — волновые. | |
Итак, всякому излучению присущи одновременно волновые и квантовые свойства. Поэтому то, как проявляет себя фотон — как волна или как частица,—зависит от характера проводимого над ним исследования. | |
Согласно квантовой гипотезе Планка-Эйнштейна свет частотой n испускается, распространяется и поглощается веществом отдельными порциями (квантами), энергия которых eо=hn (h – постоянная Планка). Эти локализованные в пространстве дискретные световые кванты, движущиеся со скоростью с распространения света в вакууме, получили название фотонов. Таким образом, распространение света можно рассматривать не как непрерывный волновой процесс, а как поток частиц – фотонов. Доказательством этих квантовых (корпускулярных) представлений о свете, как о потоке частиц, являются фотоэффект и эффект Комптона.
Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения. Явление внешнего фотоэффекта и его закономерности объяснены на основе квантовой теории фотоэффекта, согласно которой каждый квант света поглощается только одним электроном.
Энергия hn падающего на металл фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии, то есть по закону сохранения энергии:
(уравнение Эйнштейна для внешнего фотоэффекта).
Из этого уравнения следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности, то есть от числа фотонов. Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается, то при некоторой частоте n=n0 кинетическая энергия фотоэлектронов станет равной нулю и в том случае энергия фотона hn0 равна работе выхода А, из чего следует, что n0=А/h (частота n0 носит название красной границы фотоэффекта). При частоте n<n0 фотоэффекта не будет.
Масса и импульс фотона.Согласно квантовой гипотезе Планка-Эйнштейна, распространение света можно рассматривать как поток часииц – фотонов, энергия которых e=hn . Тогда из уравнения Эйнштейна взаимосвязи массы и энергии E=mc2 следует, что масса фотона:
.
Фотон движется со скоростью света с, поэтому импульс р фотона:
.
Полученные выражения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой характеристикой света – его частотой n (или его длиной волны l).
Корпускулярные свойства света проявляются в эффекте Комптона.
Эффектом Комптона называется увеличение длины волны коротковолнового электромагнитного излучения при его упругом рассеянии на свободных электронах вещества. Опыты Комптона показали, что разность длин волн рассеянного (l’) и падающего (l) электромагнитного излучения, то есть величина Dl=l’–l не зависит от длины волны l падающего излучения и природы рассеивающего вещества (РВ), а определяется только углом рассеяния q, то есть углом между направлениями лучей до и после рассеяния (рис. 29):
, где–комптоновская длина волны.
Эффект Комптона не укладывается в рамки волновой теории света, и его объяснение дано на основе квантовых представлений о природе света. Если рассматривать излучение, как поток фотонов, то эффект Комптона – это результат упругого столкновения рентгеновских фотонов со свободными электронами рассеивающего вещества. В процессе этого столкновения фотон передает электрону часть своей энергии, что ведет к увеличению длины волны при рассеянии фотона.
(На рисунке 29 введены следующие обозначения: p и p’ – импульсы фотона до и после рассеяния; pe– импульс электрона после рассеяния на нем фотона).
Исходя из законов сохранения импульса и энергии
для упругого столкновения двух частиц (рис. 29) – налетающего фотона с покоящимся свободным электроном вещества, было получено следующее выражение для величины Dl:
, где пм.
Это выражение для величины Dl, полученное на основе корпускулярных представлений о свете, оказалось аналогично приведенному выше выражению для величины Dl, полученному Комптоном экспериментально.
Следовательно, эффект Комптона является экспериментальным доказательст-вом проявления корпускулярных свойств света как потока частиц – фотонов. Итак, рассмотренные явления фотоэффекта и эффекта Комптона служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов, а, с другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую природу света. Таким образом, свет, обладая одновременно корпускулярными и волновыми свойствами, проявляет так называемый корпускулярно-волновой дуализм.
Тема 14. Тепловое излучение
Излучение света телами, обусловленное их нагреванием, называется тепловым излучением. Количественно тепловое излучение характеризуется спектраль-ной плотностью энергетической светимости тела,т.е. мощностью излучения с единицы площади поверхности тела в интервале частот единичной ширины:
, где
– энергия излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от n до n + dn .
Спектральную плотность энергетической светимостиможно представить в виде функции длины волны l , то есть в виде Rl,T, причем:
.
С помощью этой формулы можно перейти от Rn,Tк Rl,Tи наоборот.
Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимостьRT:
.
Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью Аn,T :
,
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от n до n + dn , поглощается телом.
Тело, способное поглощать полностью при любой температуре всё падающее на него излучение любой частоты, называется черным телом. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице ().
Закон Кирхгофа. Кирхгоф установил, что отношение спектральной плотности энергетической светимости Rn,Tк спектральной поглощательной способности Аn,T не зависит от природы тела; оно является для всех тел универсальной функцией rn,T частоты n (или длины волны l) и температуры Т:
.
Для черного тела , поэтому из закона Кирхгофа вытекает, что универсальная функция Кирхгофа rn,T – это спектральная плотность энергетической светимости Rn,T черного тела. Тогда выражение для интегральной энергетической светимости черного тела Reможно записать в виде:
.
Энергетическая светимость черного тела Re зависит только от температуры.
Закон Стефана – Больцмана. Согласно закону Стефана – Больцманаэнергетическая светимость черного тела Re зависит от температуры Т следующим образом: , где s – постоянная Стефана – Больцмана.
Закон смещения Вина. Из экспериментальных кривых зависимости функции rl,T от длины волны l при различных температурах (рис. 30) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют ярко выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн.
Согласно закону смещения Вина, зависимость длины волны lmax , соответствующей максимуму функции rl,T, от температуры имеет вид: , где b – постоянная Вина.
Это выражение называют законом смещения Вина, так как оно показывает смещение положения максимума функции rl,T с изменением температуры Т .
Как мы знаем, Альберт Эйнштейн в 1905 году предложил для объяснения фотоэффекта так называемую концепцию фотонов. Позже, в 1922 г., американский физик А.Комптон провел серию опытов и подтвердил ее экспериментально. Он провел исследования упругого рассеяния коротковолнового рентгеновского излучения на свободных электронах вещества (или электронах, слабо связанных с атомами) и открыл, что длина волны рассеянного изучения не соответствует ранее принятой волновой теории. Согласно ей, электроны, испытывающие воздействие периодического поля световой волны, совершают вынужденные колебания на частоте волны и поэтому излучают рассеянные волны той же частоты, следовательно, длина волны излучения при рассеянии не должна меняться.
На иллюстрации представлена схема прохождения монохроматического рентгеновского излучения с длиной волны λ0, которое исходит из трубки R, через свинцовую диафрагму. После прохождения его направляют узким пучком на слой рассеивающего вещества (алюминия, графита). Затем получившееся излучение, рассеянное под углом θ, анализируют при помощи спектрографа рентгеновских лучей S с дифракционной решеткой в виде кристалла K, помещенного на поворотный столик. Результаты опыта показывают, что в рассеянном излучении длина волны Δλ увеличивается в зависимости от угла рассеяния.
∆λ=λ-λ0=2Λsin2θ2.
Здесь параметр Λ=2,43·10–3 нм выражает так называемую комптоновскую длину волны, которая не имеет связи с свойствами рассеивающего вещества.
Определение 1
Если излучение является рассеянным, то в нем помимо спектральной линии с длиной волны λ присутствует и несмещенная линия, длина волны которой равна λ0.
Соотношение интенсивности обеих линий связано с тем, какое вещество использовано в качестве рассеивающего.
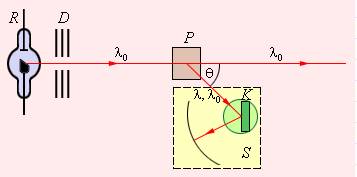
Рисунок 5.3.1. Эксперимент Комптона (схематическое изображение).
Следующие иллюстрации показывают, как распределяется интенсивность в спектре рассеянного излучения в зависимости от угла рассеивания.
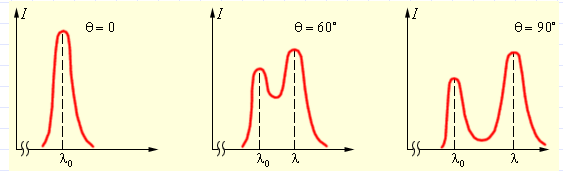
Рисунок 5.3.2. Распределение интенсивности в рассеянном излучении.
Объяснение эффекта с помощью квантовых представлений
Эффект Комптона был объяснен в 1923 году самим Комптоном и П. Дебаем, которые работали независимо друг от друга. В обоих случаях в основе объяснения лежат квантовые представления.
Определение 2
Если излучение является потоком фотонов, то эффект Комптона происходит из-за упругого столкновения свободных электронов вещества с рентгеновскими фотонами. Рассеивающие вещества имеют слабую связь между ядрами атомов и электронами, поэтому можно считать, что они имеют в составе свободные электроны. При столкновении им передается часть энергии фотонов и часть импульса.
Пример 1
Рассмотрим подробнее процесс упругого столкновения налетающего фотона с импульсом p0 =hν0c и энергией E0=hν0с электроном, у которого энергия покоя составляет Ee0=mc2. После того, как частицы столкнутся, направление движения фотона изменяется, т.е. происходит рассеяние, после чего импульс фотона становится равен p=hνc, а энергия – E=hν<E0. Что касается электрона, то, согласно релятивистской формуле, его энергия становится равной Ee=pe2c2+m2c4(буквой pe обозначен приобретенный импульс). Запишем формулу закона сохранения:
E+Ee0=E+Ee.
Иначе говоря, hυ0+mc2=hυ+pe2c2+m2c4.
Также нам понадобится закон сохранения импульса:
p0→=p→+pe→.
С помощью теоремы косинусов мы можем перевести его в скалярную форму:
pe2=hυ0c2+hυc2-2h2c2υ0υ cos θ.
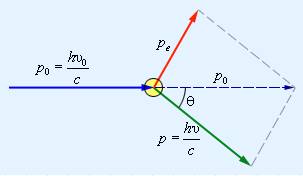
Рисунок 5.3.3. Распределение импульсов при столкновении налетающего фотона и покоящегося электрона
Теперь возьмем эти два соотношения (законы сохранения импульса и энергии), проведем несложные преобразования, исключив pe, и получим следующее:
mc2υ0-υ=hυ0υ(1-cos θ).
Перейдем от частот к волнам υ0=cλ0, υ=cλ. У нас получится выражение, совпадающее с формулой Комптона, которая была получена при эксперименте:
∆λ=λ-λ0=hmc(1-cos θ)=2hmcsin2θ2.
Проведенные теоретические расчеты, использующие квантовые представления, помогают не только объяснить эффект Комптона, но и вывести формулу нахождения длины волны с помощью фундаментальных констант m, h, c:
Λ=hmc=2,426·10-3 нм.
Почему длина части волн не изменяется?
Согласно данным опыта, в излучении после рассеяния кроме смещенной линии есть и несмещенная, длина волны излучения которой совпадает с первоначальной. Ее наличие можно объяснить тем, что часть фотонов взаимодействует с электронами, крепко связанными с ядрами атомов. Тогда происходит обмен энергии и импульса с атомом в целом, а не только с электроном. Поскольку атом весит значительно больше, то переданная энергия фотона очень мала, следовательно, длина волны λ рассеянного излучения остается практически неизменной.
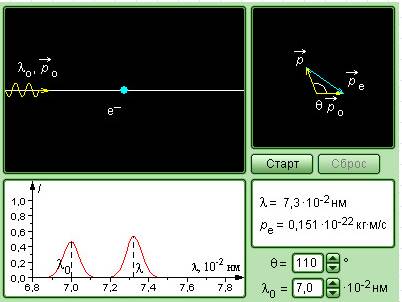
Рисунок 5.3.4. Модель комптоновского рассеяния.
Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучен различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ‘. Разность Δλ = λ – λ‘ оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λи от природы рассеивающего вещества Δλ не зависит.
Схема опыта Комптона показана на рис. 11.1.Выделяемый диафрагмами D узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся на рассеивающее вещество Р. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла К и ионизационной камеры.
На рис. 11.2 приведены результаты исследования рассеяния монохроматических рентгеновских лучей (линия Кαмолибдена) на графите. Кривая θ = 0характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс — длина волны.
Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении.
Поскольку рассеянный электрон летит со скоростью близкой к скорости света, мы должны законы сохранения энергии и импульса применять в релятивистском виде.
Пусть на первоначально покоящийся свободный электрон падает фотон с энергией ħω и импульсом p0(рис.3). Энергия электрона до столкновения равна т0с2(m0— масса покоя электрона), импульс равен нулю. После столкновения электрон будет обладать импульсом рe и энергией, равной тс2. Энергия и импульс фотона также изменятся и станут равными ħω‘ и p. Из законов сохранения энергии и импульса вытекают два равенства:
ħω + т0с2 = ħω‘ + тс2(1)
p0= рe+ p (2)
Для импульса фотона:
p0= ħk, p = ħk’,
кроме того:
Разделим равенство (1) на с и напишем его в виде
(ω/c=k). Возведение в квадрат дает
(3)
Из (2) следует, что
(4)
(θ — угол между векторами pи p; см. рис. 3).
Из сравнения выражений (3) и (4) получаем
Умножим это равенство на 2π и разделим на mckk’:
Наконец, учтя, что 2π /k =λ, придем к формуле
Δλ = λ’ – λ = λC(1 – cos θ), (5)
где
Определяемая выражением (6) величина λCназывается комптоновской длиной волны той частицы, масса т которой имеется в виду. В рассматриваемом нами случае λC— комптоновская длина волны электрона. Подстановка в (6) значений ħ, m0и с дает для λCэлектрона значение
λC = 0,0243 (7)
Результаты измерений Комптона и последующих измерений находятся в полном согласии с формулой (5), если подставить в нее значение (7) для λC .
При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Поскольку масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и λ‘ практически совпадает с λ.
§ 13. Модель атома Томсона
Согласно классическим представлениям атом мог бы испускать монохроматическую волну (т.е. спектральную линию) в том случае, когда электрон в излучающем атоме совершает гармонические колебания и, следовательно, удерживается около положения равновесия квазиупругой силой вида F = –kr, где r — отклонение электрона от положения равновесия. В 1903 г. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненный положительным электричеством шар, внутри которого находится электрон (рис. 1). Суммарный положительный заряд шара равен заряду электрона, так что атом в целом нейтрален.
Напряженность поля внутри равномерно заряженного шара определяется выражением
где е—заряд шара, R — его радиус. Следовательно, на электрон, находящийся на расстоянии r от положения равновесия (от центра шара), будет действовать сила:
В таких условиях электрон, выведенный каким-либо образом из положения равновесия, будет совершать колебания с частотой
(е—заряд электрона, m — масса электрона, R—радиус атома). Этим соотношением можно воспользоваться для оценки размеров атома. Согласно (1)
Длине волны λ = 6000 Å (видимая область спектра) соответствует ω = 3·1015 рад/с. Следовательно,
Полученное значение совпадает по порядку величины с газокинетическими размерами атомов, что можно было бы рассматривать как подтверждение модели Томсона. Однако в дальнейшем выяснилась несостоятельность этой модели, так что в настоящее время она имеет лишь исторический интерес как одно из звеньев в цепи развития представлений о строении атомов.
§ 14. Опыты по рассеянию α-частиц. Ядерная модель атома
Существовала также и другая модель атома – планетарная. Согласно этой модели в центре атома располагалось положительно заряженное ядро, вокруг которого вращались отрицательно заряженные электроны, подобно планетам, вращающимся вокруг Солнца.
Распределение положительных и отрицательных зарядов в атоме можно выяснить, произведя непосредственное опытное «зондирование» внутренних областей атома. Такое зондирование осуществили Резерфорд и его сотрудники с помощью α-частиц, наблюдая изменение направления их полета (рассеяние) при прохождении через тонкие слои вещества.
Рисунок 7
Напомним, что α-частицами называют частицы, испускаемые некоторыми веществами при радиоактивном распаде. Скорости α-частиц бывают порядка 109 см/с. В то время, когда Резерфорд приступал к своим опытам, было известно, что α-частицы имеют положительный заряд, равный удвоенному элементарному заряду, и что при потере этого заряда (при присоединении двух электронов) α–частица превращается в атом гелия.
По характеру рассеяния α–частицы можно отдать предпочтение той или иной модели строения атома (рис.2).
Опыт осуществлялся следующим образом (рис. 3). Выделяемый отверстием узкий пучок α-частиц, испускаемых радиоактивным веществом К, падал на тонкую металлическую фольгу Ф. При прохождении через фольгу α–частицы отклонялись от первоначального направления движения на различные углы φ. Рассеянные α-частицы ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции (вспышки) наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр рассеивающей фольги, и устанавливать таким образом под любым углом φ. Весь прибор помещался в откачанный кожух, чтобы устранить рассеяние α-частиц за счет столкновений с молекулами воздуха.
Оказалось, что некоторое количество α-частиц рассеивается на очень большие углы (почти до 180°). Проанализировав результаты опыта, Резерфорд пришел к выводу, что столь сильное отклонение α-частиц возможно только в том случае, если внутри атома имеется чрезвычайно сильное электрическое поле, которое создается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Основываясь на этом выводе, Резерфорд предложил в 1911 г. ядерную модель атома. Согласно Резерфорду атом представляет собой систему зарядов, в центре которой расположено тяжелое положительное ядро с зарядом Zе, имеющее размеры, не превышающие 10-12 см, а вокруг ядра расположены Z электронов, распределенных по всему объему, занимаемому атомом. Почти вся масса атома сосредоточена в ядре.
Исходя из таких предположений, Резерфорд разработал количественную теорию рассеяния α-частиц и вывел формулу для распределения рассеянных частиц по значениям угла φ. При выводе формулы Резерфорд рассуждал следующим образом. Отклонения α -частиц обусловлены воздействием на них со стороны атомных ядер. Заметного отклонения из-за взаимодействия с электронами не может быть, поскольку масса электрона на четыре порядка меньше массы α -частицы. Когда частица пролетает вблизи ядра, на нее действует кулоновская сила отталкивания
В этом случае траектория частицы представляет собой гиперболу. Угол между асимптотами гиперболы обозначим буквой θ (рис. 14.2). Этот угол характеризует отклонение частицы от первоначального направления. Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем, естественно, сильнее она отклоняется (тем больше θ). Между величинами b и θ имеется простое соотношение, которое легко установить решая задачу о движении частицы в центральном поле:
Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая частица при прохождении через него пролетала вблизи только одного ядра, т. е. чтобы каждая частица претерпевала лишь однократное рассеяние. Для того чтобы испытать рассеяние на угол, лежащий в пределах от θ до θ +dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b+db (рис. 4), причем dθ и db, как следует из (1), связаны соотношением
Знак минус в этом выражении обусловлен тем, что с увеличением b
(т.е. при db > 0) угол отклонения убывает (dθ < 0). В дальнейшем нас будет интересовать лишь абсолютное значение db в функции от θ и dθ, поэтому знак минус мы не будем учитывать.
Обозначим площадь поперечного сечения пучка α-частнц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка можно представить в виде пSа, где п — число атомов в единице объема, а – толщина фольги. Если α-частицы распределены равномерно по сечению пучка и число их очень велико (что имеет место на самом деле), то относительное количество α-частиц, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db (и, следовательно, отклоняющихся в пределах углов от θ до θ+dθ), будет равно (см. рис. 5):
В этом выражении dNθ — поток частиц, рассеиваемых в пределах углов от θ до θ+dθ, N — полный поток частиц в пучке.
Заменив в формуле (2) b и db через θ и dθ в соответствии с (1) и (2), получим
Преобразуем множители, содержащие угол θ:
С учетом этого преобразования
Выражение дает телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Поэтому можно написать:
Мы получили формулу Резерфорда для рассеяния α-частиц. В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени. В условиях опыта (см. рис. 3) счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла (определявшегося площадью экрана Э и расстоянием его от фольги), поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально . Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и скорости α-частиц также оказалась -в соответствии с формулой (4).
Справедливость теории, исходящей из кулоновского взаимодействия между α-частицей и ядром атома, свидетельствует о том, что даже отбрасываемая в обратном направлении α-частица не проникает в область положительного заряда атома. Вместе с тем, летящая точно по направлению к ядру α-частица подошла бы кего центру на расстояние, которое можно определить, приравняв кинетическую энергию α-частицы потенциальной энергии взаимодействия α-частицы с ядром в момент полной остановки частицы:
— минимальное расстояние между центрами α-частицы и ядра,
.
Итак, результаты опытов по рассеянию α-частиц свидетельствуют в пользу ядерной модели атома, предложенной Резерфордом рис.7.
Однако ядерная модель оказалась в противоречии с законами классической механики и электродинамики. Поскольку система неподвижных зарядов не может находиться в устойчивом состоянии, Резерфорду пришлось отказаться от статической модели атома и предположить, что электроны движутся вокруг ядра, описывая искривленные траектории. Но в этом случае электрон будет двигаться с ускорением, в связи с чем, согласно классической электродинамике, он должен непрерывно излучать электромагнитные (световые) волны. Процесс излучения сопровождается потерей энергии, так что электрон должен в конечном счете упасть на ядро (рис. 7).
Date: 2015-05-18; view: 598; Нарушение авторских прав