Какие свойства силы бывают
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
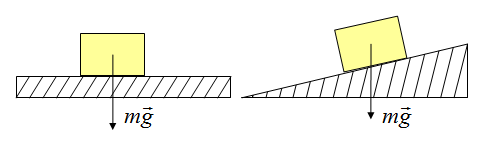
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
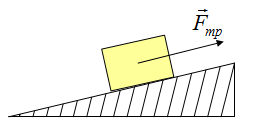
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
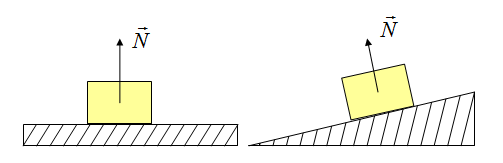
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
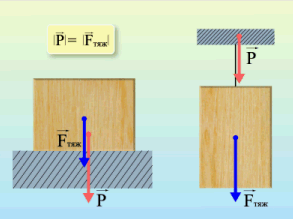
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
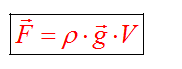
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
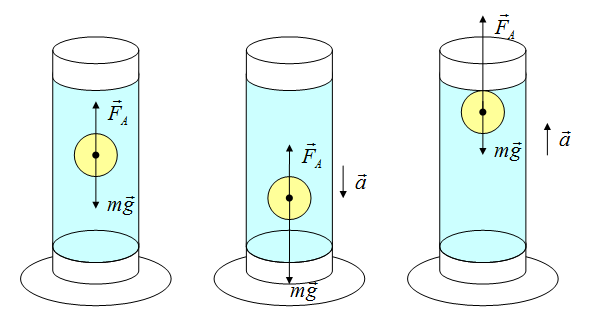
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
 Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Сила характеризует количественную сторону механического взаимодействия. Таким образом, когда говорят, что на тело действуют силы, то это значит, что на него воздействуют другие тела (или физические поля). Не всегда, впрочем, сила действительно приводит к изменению движению тела; такое изменение может блокироваться действием других сил. С учетом сказанного запишем:
Сила (ньютонова) – мера механического воздействия на некото- рое материальное тело со стороны другого материального тела (или физического поля); она характеризует интенсивность и направление этого воздействия. Это, разумеется, не определение, а лишь пояснение к понятию силы. Поскольку понятие силы – фундаментальное, то его точный смысл раскрывается в аксиомах механики.
Пока же мы отметим вот что. Оговорка “ньютонова” сделана потому, что в динамике мы встретимся с другими величинами, также именуемыми силами, которые, однако, не являются мерами механического взаимодействия. В этом же семестре речь будет идти именно о ньютоновых силах, и мы для краткости будем называть их просто силами.
Далее, под словом “мера” в механике и в физике понимается физическая величина, которая служит для количественного описания какого-либо свойства или отношения. В данном случае речь идет об описании именно механического взаимодействия (а бывают еще, как Вы знаете, и другие взаимодействия – тепло- вые, химические и прочие).
В физике элементарных частиц выделяют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Эти четыре взаимодействия лежат в основе всех наблюдаемых явлений – относящихся как к механике, так и к другим разделам естествознания.
Однако в макромире фундаментальные взаимодействия проявляются, как правило, опосредованно, и нам приходится иметь дело со значительно более широким перечнем взаимодействий (уже не обязательно фундаментальных). Если говорить о механических взаимодействиях, то речь может идти о силах различного происхождения.
Примеры сил: силы тяжести, силы упругости, архимедовы силы, силы сопротивления среды и др. В большинстве задач механики, впрочем, физическая природа тех или иных сил обычно интереса не представляет.
Ещe мы, поясняя понятие силы, говорили об интенсивности и направлении воздействия. Это означает, что сила является векторной величиной. Именно, это – вектор, приложенный к определeнной точке материального тела. Поэтому можно говорить о таких характеристиках силы.
Сила характеризуется:
1) величиной (модулем);
2) направлением;
3) точкой приложения.
К сожалению, на экзамене нередко приходится встречаться с полным пренебрежением к этому правилу. В лучшем случае экзаменатор в этой ситуации поступит так: вздохнет и попросит студента быстренько проставить обозначения векторов в тексте ответа на поставленный вопрос. Если студент не сумеет правильно проставить обозначения – это первый шаг на пути к получению “двойки”. Поэтому, пожалуйста, не игнорируйте в своих конспектах черту, если она написана на доске.
Круглые скобки с запятой в середине обозначают скалярное произведение векторов (запятая при этом разделяет сомножители). Обратите внимание: во многих книгах скалярное произведение обозначается иначе – точкой между век- торами, причем точку обычно можно опустить.
Но мы будем придерживаться именно таких обозначений (они тоже достаточно распространены). Помимо всего прочего, они позволяют избежать путаницы (ведь скалярное произведение векторов нужно отличать от обычного произведения двух скаляров).
Пока мы говорили только о векторе силы. Но понятие силы не сводится к понятию ее вектора. Важна еще и точка приложения силы: ведь если тот же по величине и направлению вектор силы приложить в другой точке тела, то его движение может измениться.
В геометрии принята следующая терминология. Свободный вектор (или просто вектор) – вектор, характеризуемый только модулем и направлением. Связанный вектор – вектор, характеризуемый еще и точкой приложения. Иногда используют такие обозначения.
Через u—.A обозначается связанный вектор, получаемый, если свободный вектор u— приложить в точке A. Обратите внимание: здесь точка пишется не в середине строки (как при умножении чисел), а на ее нижней линии. Таким образом, можно сделать следующий вывод. Итак, сила – связанный вектор (полное обозначение: F—-.A).
Там, где нам потребуется подчеркнуть наличие у силы определенной точки приложения, мы будем пользоваться именно этим полным обозначением. Там, где точка приложения силы будет заранее оговорена, мы будем применять сокращенное обозначение, обозначая силу просто F—- (т.е. так же, как и вектор силы). О точке приложения силы нужно сказать следующее: Если сила действует на материальную точку, то точкой приложения служит сама эта точка.
Если сила действует на материальное тело, то точкой приложения служит точка тела (она может меняться с течением времени). В общем случае точка приложения силы не может лежать вне тела. Если тело – абсолютно твердое, то данное ограничение можно снять; но об этом мы будем говорить позже.
Возникает вопрос: а как можно на практике задать точку приложения силы? Любую точку можно задать, например, ее радиус-вектором, проведенным из некоторого полюса. Полюс – произвольно выделенная точка (положение которой обычно предполагается известным).
Раз здесь говорится “обычно”, то текст в скобках Вы вполне можете игнорировать. Часто бывает так: взяли некоторую точку и объявили ее полюсом (и будет она с этого времени считаться таковым). Но для задания положения точки приложения силы нам как раз нужно знать положение полюса. Можно – но не обязательно – принять за полюс начало системы координат.
Употребляют оба обозначения, но первое предпочтительнее: вектор обозначается одной буквой, а буква “r” напоминает, что речь идет именно о радиус- векторе, или шестью скалярами (Fx , Fy , Fz , xA , yA , zA ). Это – удобно, и так поступают часто. Но задать силу можно также иным способом, который мы рассмотрим в следующем пункте.
Статика
В статике изучают свойства сил и определяют условия равновесия тел.
Свойства силы и пар сил.
Сила есть мера механического действия одного тела на другое, которая проявляется в виде деформации или изменения движения тела.
Сила есть приложенный вектор, изображаемый из точки приложения силы, определяемый двумя векторами: вектором и радиус-вектором точки её приложения.
Силу можно задавать в декартовой системе отсчета шестью скалярами: тремя проекциями силы на оси координат X, Y, Z и тремя координатами x,y,z точки приложения силы.
Силу, приложенную к абсолютно твердому телу можно считать скользящим вектором, т.е. силу можно перемещать вдоль линии её действия, минуя точку приложения, поскольку известно, что при этом механическое действие силы на тело, способность разгонять и раскручивать тело не меняются. Параллельный перенос силы не допустим — при переносе силы на параллельную линию, изменяется её вращательная способность. Силу можно раскладывать на составляющие, т.е. – заменять несколькими силами, приложенными в прежней точке тела.
Нередко, заменяют тремя составляющими:
.
Пару сил можно считать приложенной в любом месте твердого тела, момент пары есть свободный вектор, который обычно изображается из точки приложения одной из двух сил, либо – из середины плеча пары.
Внешние силы, приложенные к телу, разделяют на неизвестные силы (реакции опор, связей) и известные силы (приложенные нагрузки). В некоторых случаях известно направление реакции опоры, тогда имеем только одну неизвестную – модуль реакции опоры.
Применяется следующий прием: если в каком-либо направлении связь не препятствует бесконечно малому перемещению тела, то реакция этой связи перпендикулярна этому направлению. Система сил, приложенных к телу, называется плоской, если все неизвестные и известные силы расположены в некоторой одной плоскости 0xy.
Скалярным моментом силы относительно точки O называется произведение модуля силы и плеча силы со знаком, определяющим направление кажущегося вращения силы вокруг точки
Теорема. Если тело находится в состоянии равновесия ( не движется ), то система всех приложенных к нему внешних сил удовлетворяет трем алгебраическим уравнениям равновесия, а именно, равны нулю сумма моментов всех приложенных сил и суммы проекций сил на две оси координат :
Пример 1
| Рис.1 Рисунок к задаче |
Криволинейный стержень ОАВ, опирающийся на каток и шарнир находится в состоянии равновесия. Определить реакции связей. Задан линейные размеры, и величины сосредоточенной силы и интенсивность распределенной нагрузки , а также — момент пары приложенных сил (Рис.1)
Решение.
Освободим тело от связей, но сохраним действие связей и заменим нагрузку интенсивностью на равнодействующую , приложенную к середине участка приложения распределенной нагрузки (рис. 2). Неизвестные реакции связей направляем в положительную сторону. Продолжим пунктиром линии действия сил и покажем плечи сил относительно точки О, отметим знаком (±) направления вращения силы вместе с плечом вокруг точки О. А также перенумеруем все силы, в частности переобозначим :
| Рис.1 Реакции опор и плечи сил |
плечо силы
– плечо силы , знак (-)
– плечо , знак (+)
– плечо , знак (+), где
– плечо , знак (-)
Составим в табличной форме два уравнения проекций и уравнение моментов относительно точки :
Далее, выражая длину плеч сил через известные размеры и углы, получим систему трех линейных алгебраических уравнений относительно трех неизвестных реакций опор
Замечание: момент любой силы можно также находить и методом разложения на составляющие, что упрощает вычисление плеч сил.
Например, имеем (рис. 3)
| Рис. 3 Момент силы как сумма моментов ее проекций |
Пример 2
| Рис. 4 Рисунок к задаче |
Консольная балка, закрепленная в стене. (рис. 4), нагруженная растягивающей силой F и поперечной расперделенной нагрузкой q (например — собственным весом).
Решение
В заделке возникает реакция в виде составляющих , а так же — пара сил с неизвестным моментом удерживающие балку от вращения. Относительно О имеем плечи сил (со знаком) и уравнения равновесия в табличной форме:
В результате получаем систему уравнений вида
Отсюда окончательно получаем неизвестные реакции опоры:
Ма́сса — скалярная физическая величина, одна из важнейших величин в физике. Первоначально она характеризовала «количество вещества» в физическом объекте. Масса — это мера инертности тела. Масса аддитивна и инвариантна относительно смены системы отсчета
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: . может быть только положительной величиной, либо равной нулю.
Сила — Сила — векторная величина, характеризующая механическое действие одного тела на другое, которое проявляется в деформациях рассматриваемого тела и изменении его движения относительно других тел.Сила характеризуется модулем и направлением. Модуль и направление силы не зависят от выбора системы отсчета. Способы измерения силы: динамометром. Единица измерения силы в СИ — 1 Н.
Свойства силы:
1. Сила является функцией скорости и положения материальной точки.
F= f((Vx;Vy;Vz), x, y, z).
2. Сила, с которой одна частица действует на другую зависит от R векторов и скоростей только этих двух частиц, присутствие других частиц на эту силу не влияет. Это свойство силы называют принципом парности взаимодействия. Следствие из него называется принципом суперпозиции. 3. 3-й закон Ньютона — сила действия равна силе противодействия
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: “результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил” (Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.)
Силы в механике: 1) Сила тяготения, гравитационная. . 2) Сила упругости, электромагнитная. .
3)Сила трения, сухого, жидкого. электромагнитная.
Законы классической механики Ньютона. Условия применимости законов Ньютона. Основной закон классической динамики материальной точки. Решение основной задачи динамики.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Свойство тела сохранять свое состояние называется инертностью. Поэтому первый закон Ньютона называют законом инерции.
Второй закон Ньютона: ускорение, приобретаемое материальной точкой или телом, пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Третий закон Ньютона: Действие равно противодействию: F = -F.
Условия применимости законов Ньютона: В инерциальных системах отсчета и при движении со скоростями, много меньшими скорости света.
Основной закон классической динамики МТ — Масса движущихся релятивистских частиц зависит от их скорости:
где m0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Решение основной задачи динамики –
1) Зная массу точки и ее движение, найти силы, действующие на точку или их равнодействующую.
1. Составить дифференциальные уравнения
2. По известному движению материальной точки найти проекции ускорения на оси координат, которые выбраны для составления дифференциальных уравнений.
3. Подставляя проекции ускорения в составленные дифференциальные уравнения, найти проекции равнодействующей сил, приложенных к точке.
4. Используя дополнительные условия, например, направления реакций связей, определить по равнодействующей силы, приложенные к точке. Если на точку действует одна сила, то для нахождения величины и направления этой силы можно использовать формулы (1) — (3), полученные для равнодействующей.
5. Проанализировать полученное решение.
2) Зная приложенные к точке силы, а также ее массу, определить ее движение, описываемое кинематическими уравнениями.
1. Составить дифференциальные уравнения для конкретного случая движения материальной точки
2. Определить и записать начальные условия задачи.
3. Проинтегрировать дифференциальные уравнения в соответствии с методами, известными из курса математики, определяя постоянные интегрирования с помощью начальных условий, для нахождения единственногорешения.
4. Проанализировать полученный в решении закон движения материальной точки в зависимости от конкретных вопросов в задаче и найти ответы на них.
5.системой материальных точек называется такая их совокупность,в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы.
Какие взаимодействия относятся к фундаментальным? На каких расстояниях проявляются фундаментальные взаимодействия? Какова относительная интенсивность фундаментальных взаимодействий?
Фундаментальные воздействия
1)слабое (менее 10-15) интнесивность – 10-13
2)сильное (менее 10-15) интнесивность – 1
3) Электростатическое (от 0 до беконеч.) интнесивность – 10-2
4) Гравитационное (от 0 до беконеч.) интнесивность – 10-38
Определение момента импульса материальной точки и момента силы. Проекция векторов момента импульса и момента силы на выбранную ось Уравнение моментов для материальной точки. При каких условиях сохраняется момент импульса материальной точки?
Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Моментом импульса материальной точки А относительно неподвижной точки Оназывается физическая величина, определяемая векторным произведением:
L = [rp] = [r,mv],
где г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс
Вектор будет направлен вдоль нормали к плоскости, образованной векторами и ,направление которого определяется по правилу буравчика.
Условие сохранения — остается постоянной, пока на систему не воздействуют внешние силы
5. Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз)
Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой.
Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.
Цен-
тром масс (или центром инерции)
системы материальных точек называет-
ся воображаемая точка С, положение
которой характеризует распределение
массы этой системы. Ее радиус-вектор
равен
Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Скорсть центра масс
Для непрерывного распределения массы с плотностью r . Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если не параллельны, то центр масс и центр тяжести не совпадают.
Взяв производную по времени от , получим:
т.е. полный импульс системы равен произведению ее массы на скорость центра масс.
Подставляя это выражение в закон изменения полного импульса, находим:
Центр масс системы движется как частица, в которой сосредоточена вся масса системы и к которой приложена результирующая внешних сил.
При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс.
Так как , то центр масс замкнутой системыдолжен сохранять состояние покоя или равномерного прямолинейного движения, т.е. =const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.
Rс(t1) = Rc(t2) закон сохранения координаты центра масс
8. Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии
Потенциальная сила — сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Потенциальное (консервативное) силовое поле:Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.
Введения понятия потенц. Энергии через работу сил — Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля.
Связь силы и потенциальной энергии — Каждой точке потенциального поля соответствует некоторое значение силы , действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой и U должна быть связь , с другой стороны, dA = –dU,
Механика абсолютно твердого тела.
1 Модель абсолютно твердого тела (определение). Уравнение движения АТТ на
примере двух жестко связанных материальных точек, вращающихся вокруг оси. Введение понятия момента инерции.
В механике вводится еще одна модель —
абсолютно твердое тело. Абсолютно
твердым называют тело, которое ни
при каких условиях не может деформи-
роваться и при всех условиях расстоя-
ние между двумя точками (или точнее
между двумя частицами) этого тела ос-
тается постоянным.
2 Применение момента инерции АТТ при вращательном движении. Его физический
