Какие свойства произведения векторов вы знаете
В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.
Действия над векторами
Определение
Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ — начало, точка
$B$ — конец вектора.
Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец — с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.
Свойства операции сложения:
1° $overline{a}+overline{b}=overline{b}+overline{a}$ — коммутативность
2° $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ — ассоциативность
3° $overline{a}+overline{0}=overline{a}$
4° $overline{a}+(-overline{a})=overline{0}$
Определение
Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.
Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:
- $overline{b} | overline{a}$
- $|overline{b}|=|alpha||overline{a}|$
- $overline{a} uparrow uparrow overline{b}$, если
$alpha>0$,
$overline{a} uparrow downarrow overline{b}$, если
$alpha
Свойства умножения вектора на число:
1° $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$
2° $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$
3° $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$
4° $1 cdot overline{a}=overline{a}$
5° $-1 cdot overline{a}=-overline{a}$
6° $0 cdot overline{a}=overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:
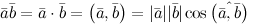
Свойства скалярного произведения:
1° $(overline{a}, overline{b})=(overline{b}, overline{a})$ — симметричность.
2° $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.
3° Если $overline{a} neq overline{0}$, то 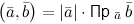
4° Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.
5° $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$
6° $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$
7° $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$
Определение
Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
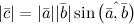 .
.
Свойства векторного произведения:
1° $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$
2° $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$
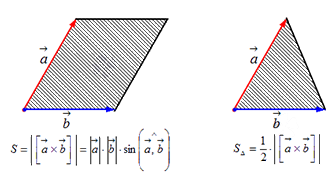
3° Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.
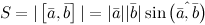
4° $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$
5° $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Свойства смешанного произведения:
1° $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2° $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3° Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4° Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c})
5° $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6° $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7° $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8° $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9° $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10° Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
Вы поняли, как решать? Нет?
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
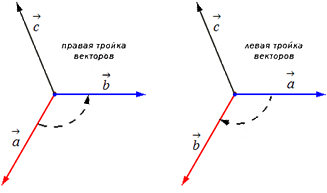
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
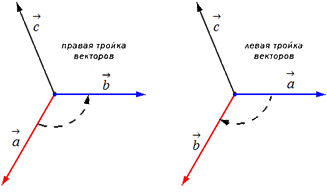
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1
Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
- его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Определение 2
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативности
По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Пример 1
Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2
В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Пример 3
Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6..
Пример 4
В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Пример 5
Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.
Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Определение 3
Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
Векторное произведение в трёхмерном евклидовом пространстве
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.
Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.
Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.
Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.
История[править | править код]
Векторное произведение было введено У. Гамильтоном в 1846 году[1] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[2].
Определение[править | править код]
Векторным произведением вектора на вектор в трёхмерном евклидовом пространстве называется вектор , удовлетворяющий следующим требованиям:
Обозначения:
Замечания[править | править код]
В качестве определения можно использовать описанное далее выражение векторного произведения в координатах в правой (или левой) прямоугольной системе координат.
Также в качестве исходного определения может быть взят набор алгебраических свойств векторного произведения.
Правые и левые тройки векторов в трёхмерном евклидовом пространстве[править | править код]
Рассмотрим упорядоченную тройку некомпланарных (линейно независимых) векторов в трёхмерном евклидовом пространстве. В ориентированном пространстве такая тройка векторов будет либо «правой», либо «левой».
Геометрическое определение[править | править код]
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если с конца вектора кратчайший поворот от вектора к вектору виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.
Определение с помощью руки[править | править код]
Другое определение связано с правой рукой человека, откуда и берётся название. На рисунке тройка векторов , , является правой.
Алгебраическое определение[править | править код]
Существует также аналитический способ определения правой и левой тройки векторов, который требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора , второй — вектора , третьей — вектора . Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Замечания[править | править код]
Определения «правой» и «левой» тройки векторов зависят от ориентации пространства, но не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого определение самого векторного произведения. При этом формулы выражения координат векторного произведения через координаты исходных векторов будут отличаться знаком в правой и левой прямоугольной системе координат.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
При заданной ориентации пространства система координат называется правой (левой), если тройка из векторов с координатами , , является правой (левой).
Геометрическое определение и определение с помощью руки сами задают ориентацию пространства. Алгебраическое определение задаёт способ разбить тройки некомпланарных векторов на два класса одинаково ориентированных векторов, но оно не задаёт ориентацию пространства, а использует уже заданную — ту, на основании которой данная система координат считается правой или левой. При этом, если ориентация системы координат неизвестна, можно сравнивать знак определителя со знаком определителя другой тройки некомпланарных векторов, ориентация которой известна — если знаки совпадают, то тройки одинаково ориентированы, если знаки противоположны — тройки ориентированы противоположно.
Свойства[править | править код]
Геометрические свойства векторного произведения[править | править код]
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов так же, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения[править | править код]
Далее и обозначают соответственно векторное и скалярное произведение векторов и .
Выражение в координатах[править | править код]
В правом ортонормированном базисе[править | править код]
Если два вектора и представлены в правом ортонормированном базисе координатами
то их векторное произведение имеет координаты
Для запоминания этой формулы удобно использовать мнемонический определитель:
где , , , или
где — символ Леви-Чивиты.
В левом ортонормированном базисе[править | править код]
Если базис левый ортонормированный, то векторное произведение в координатах имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
В произвольной аффинной системе координат[править | править код]
Векторное произведение в произвольной аффинной системе координат имеет координаты
Вариации и обобщения[править | править код]
Кватернионы[править | править код]
Координаты векторного произведения в правом ортонормированном базисе можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме[править | править код]
Векторное произведение двух векторов в координатах в правом ортонормированном базисе можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в эпиполярной геометрии[en]).
Из общих свойств векторного произведения следует, что
и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «БАЦ минус ЦАБ»).
Распространение на матрицы[править | править код]
В трёхмерном случае можно определить в координатах в произвольном базисе векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот.
Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева (базис считается правым ортонормированным). В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём[править | править код]
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
.
Эта конструкция называется внешним произведением.
Для двумерного случая операция
.
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению.)
Алгебра Ли векторов[править | править код]
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также[править | править код]
Произведения векторов
Другое
- Ротор
- Дивергенция
Примечания[править | править код]
Литература[править | править код]
- Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. АН СССР: Изд-во «НАУКА», М. 1965.
Ссылки[править | править код]
- Многомерное векторное произведение
- Векторное произведение и его свойства. Примеры решения задач
- В. И. Гервидс. Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Дата обращения 3 мая 2011.
