Какие свойства параллельных прямых включены в их определение и аксиому
Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.
Определение 1
Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.
Пример 1
Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.
Определение 2
Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.
Пример 2
При параллельных прямых их секущая образует равные накрест лежащие углы.
Определение 3
Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.
Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.
Аксиома параллельных прямых
Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Теорема 1
Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Аксиома доказательства не требует.
Свойства параллельных прямых
Теорема 2
Свойство1. Свойство транзитивности параллельности прямых:
Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.
Свойства требуют доказательств.
Доказательство:
Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.
Для доказательства будем пользоваться противоположным суждением:
Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.
Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.
Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.
Теорема 3
Свойство 2.
Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.
Доказательство:
Пусть имеются две параллельные прямые $а$ и $b$. Также пусть имеется некоторая прямая $с$, которая пересекает одну из параллельных прямых, например, прямую $а$. Необходимо показать, что прямая $с$ пересекает и вторую прямую – прямую $b$.
Построим доказательство методом от противного.
Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. е. являются параллельными ей. Но такая ситуация противоречит аксиоме параллельных прямых. Значит, предположение было неверным и прямая $с$ пересечет прямую $b$.
Теорема доказана.
Свойства углов, которые образуют две параллельные прямые и секущая:
накрест лежащие углы равны,
соответственные углы равны,
* сумма односторонних углов равна $180^{circ}$.
Пример 3
Даны две параллельные прямые и третья прямая, перпендикулярная одно из них. Доказать, что эта прямая перпендикулярна и другой из параллельных прямых.
Доказательство.
Пусть имеем прямые $а parallel b$ и $с perp а$.
Поскольку прямая $с$ пересекает прямую $а$, то согласно свойству параллельных прямых она будет пересекать и прямую $b$.
Секущая $с$, пересекая параллельные прямые $а$ и $b$, образует с ними равные внутренние накрест лежащие углы.
Т.к. $с perp а$, то углы будут по $90^{circ}$.
Следовательно, $с perp b$.
Доказательство завершено.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Аксиома параллельных прямых
Рассмотрим произвольную прямую 
и точку М, не лежащую на ней (Рис.1).
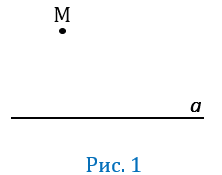
Докажем, что через точку М можно провести прямую, параллельную прямой . Для этого проведем через точку М две прямые: сначала прямую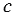 
перпендикулярно к прямой , а затем прямую 
перпендикулярно к прямой 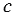(Рис.2). А из того, что две прямые и перпендикулярны к третьей прямой 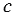следует, что они параллельны (
).
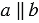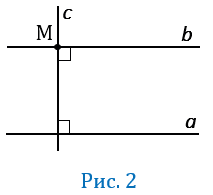
Возникает вопрос: можно ли через точку М провести еще одну прямую, параллельную прямой ?
Если прямую «повернуть» на какой-то угол вокруг точки М, то она пересечет прямую (прямая ‘ на рис.3).
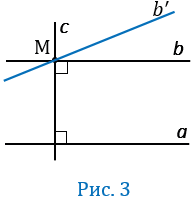
То естьнам кажется, что через точку М нельзяпровести прямую отличную от прямой , параллельную прямой . Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы параллельных прямых
10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Дано: ,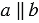 
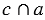= М (Рис.4).
Доказать: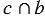 
.
Доказательство:
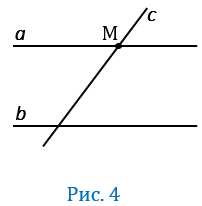
Если мы предположим, что прямая 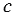не пересекает прямую , то прямая 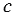будет параллельна прямой , а по условию через точку М проходит прямая параллельная прямой , значит получим, чточерезточку М будут проходить две прямые и 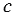параллельные прямой (Рис.5).
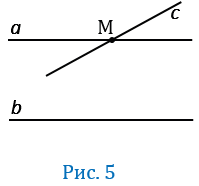
Но это противоречит аксиоме параллельных прямых, значит, наше предположение неверно, и прямая 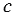пересекает прямую , т.е. 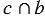. Что и требовалось доказать.
20. Если две прямые параллельны третьей прямой, то они параллельны.
Дано: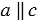 
, 
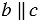(Рис.6).
Доказать: .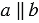
Доказательство:
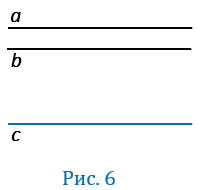
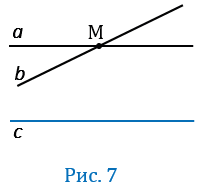
Предположим, что прямые и не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).
Тогда получим, что через точку М проходят две прямые и параллельные прямой 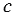, т.к. по условию 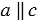и 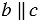. Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые и параллельны, т.е. 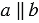. Что и требовалось доказать.
Следствие — утверждение, которое выводится непосредственно из аксиом или теорем.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 196,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 199,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 217,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 218,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 279,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 282,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 567,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1148,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Юлия Ш. · 29 апреля 2019
14,6 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас…
Паралелльные прямые — прямые, которые не пересекаются в какой угодно точке, сколько бы их не продолжали, достаточно абстрактное понятие.
Параллельные лучи — лучи, прямые которых не пересекаются в какой угодно точке, сколько бы их не продолжали.
Угол не может быть образован двумя параллельными прямыми, потому что определение параллельных прямых противоречит определению угла, если говорить об углах между ними, то:
- Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.
- Если две параллельные прямые пересечены секущей, то соответственные углы равны.
- Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
- Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Свойства параллельных прямых:
Если параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если параллельные прямые пересечены секущей, то соответственные углы равны.
Если параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Признаки параллельности прямых:
Если накрест лежащие углы, образованные при пересечении двух прямых… Читать далее
Если прямые пересечены секущей и накрест лежащие углы равны значит прямые паралельны
Почему через две параллельные прямые можно провести только одну плоскость?
Давайте проведём плоскость через две параллельные прямые а затем станем её перемещать, не меняя положения прямых.
Если вращать плоскость вокруг одной из прямых, вторая прямая будет лежать на плоскости только в одном случае — изначально данном.
Если вращать плоскость вокруг другой оси, параллельной нашим прямым, это будет происходить с обеими прямыми.
Если вращать вокруг вращать вокруг непараллельной оси, прямые будут пересекать плоскость в любом случае, кроме данного.
И, наконец, если просто перемещать плоскость в пространстве, прямые не будут лежать на плоскости вообще.
Таким образом, мы перебрали все возможные плоскости в пространстве, и лишь на одной из них лежат обе наши прямые. Следовательно, через две параллельные прямые можно перевести только одну плоскость
Прочитать ещё 1 ответ
Что имел в виду К. Поппер, утверждавший, что «Платон — первый полит. идеолог, […] придумавший «концентрационные лагеря»?
Основная мысль Поппера состоит в том, что политическая модель Платона, описанная в «Государстве» и «Законах», является теоретическим обоснованием тоталитарного государства.
Действительно, при всей проницательности Платона относительно политики и при вполне справедливом указании в «Государстве» на проблемы существующих политических режимов, на жизнь в рамках которых мы обречены (идеи Платона в этом отношении, к слову сказать, вполне актуальны и могут быть использованы при осмыслении современной политики), лекарство от «порочных форм правления», предлагаемое Платоном, кажется, во многом хуже самой болезни.
Прежде всего, политический идеал Платона, вне всякого сомнения, тяготеет к тоталитарной модели, при которой индивид во всех отношениях ставится в подчинение государству. Сам Платон ясно проговаривает это в седьмой книге «Государства»:
«…закон ставит своей целью не благоденствие одного какого-нибудь слоя населения, но благо всего государства. То убеждением, то силой обеспечивает он сплоченность всех граждан, делая так, чтобы они были друг другу взаимно полезны в той мере, в какой они вообще могут быть полезны для всего общества. Выдающихся людей он включает в государство не для того, чтобы предоставить им возможность уклоняться куда кто хочет, но чтобы самому пользоваться ими для укрепления государства».
Что же касается «концентрационных лагерей», то ближайший аналог подобной политики, как мне кажется, можно усмотреть в пятой книге «Законов», где Платон пишет о необходимости «очищения» государства от неблагонадёжных людей, причём не только от преступников, но и, например, от потениальных бунтарей.
«Относительно очищений государства дело обстоит так: полных очищений существует немало; одни из них легче, другие более тягостны. Тягостные и наилучшие мог бы установить лишь тот, кто одновременно является и тираном и законодателем. Законодатель, лишенный тиранической власти, при установлении нового государственного строя и законов должен удовольствоваться самыми мягкими способами очищений. Наилучший способ мучителен совершенно также, как бывает, когда принимают подобного рода лекарства. При этом способе правосудие влечет за собой справедливое возмездие; возмездие заканчивается смертью или изгнанием. Так обыкновенно отделываются от величайших, к тому же неисцелимых, преступников, чрезвычайно вредных для государства. Более мягкий способ очищения заключается у нас вот в чем: если неимущие люди, следуя за своими вождями, выкажут из-за недостатка воспитания склонность выступить против имущих, это станет болезнью, вкравшейся в государство. Поэтому их надо выслать прочь, делая это, однако, в высшей степени дружелюбно и смягчая их удаление названием «переселение». Так или иначе всякому законодателю надлежит это сделать сразу».
Почему кажется, что линии на этой картинке не параллельны, хотя они параллельны?
интеллектуал. дизайнер. меломан. мизантроп.
Потому что мозг человека настроен иначе. Он не рассчитан на восприятие геометрических узоров такого типа — различные способы анализа изображения начинают конфликтовать друг с другом. Миллионы лет человек приспосабливаться к трёхмерному миру (перспектива) освещённому сверху вниз. Эта привычка помогает быстро ориентироваться в пространстве, но мешает решению визуальных ребусов. 🙂
Вот простейший случай:
Иллюзия стены кафе — оптическая иллюзия, создаваемая за счёт совместного действия разных уровней нейронных механизмов: нейронов сетчатки и нейронов зрительной коры.
С первого взгляда кажется, что серые линии между чёрными и белыми квадратами расположены под углом, но если присмотреться то можно увидеть что линии абсолютно ровные. Мозг, сбитый с толку контрастными и близко расположенными квадратами, видит серые линии как часть мозаики, выше или ниже квадратов.
Иллюзия была открыта в 1973 году исследователем Ричардом Грегори из Бристольского университета который теперь является почетным профессоромнейропсихологии. Посмотрев на одну из стен кафе, исследователь обнаружил причудливую особенность рисунка на стене. В материале и конструкции стены не было ничего необычного, все дело в рисунке из черных и белых кирпичиков, ряды которых были сдвинуты на пол-ширины кирпича и разделены тонкой полоской раствора. Эффект оказался гипнотическим. Из-за того, что иллюзия была найдена на стене кафе, она и получила своё название.
Вот более весёлый вариант:
Что такое параллельность плоскостей?
Образование: высшее (бакалавр + магистр). Увлечения: спорт, путешествие, кофе:)
Определение: Две плоскости называются параллельными, если они не имеют общих точек.
Свойства:
1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны;
2. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну;
3. Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны;
4. Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.
Признак:
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.
Источник: https://ru.wikipedia.org/wiki/Параллельность_плоскостей .
Две прямые, лежащие на одной плоскости, либо имеют только одну общую точку, либо не имеют ни одной общей точки.
В первом случае говорят, что прямые пересекаются, во втором случае — прямые не пересекаются.
На плоскости две прямые (a) и (b), которые не пересекаются, называются параллельными и обозначаются a∥b.
Обрати внимание!
Если рассмотреть прямые, которые не лежат в одной плоскости, то возможна ситуация, что прямые не пересекаются, но они и не параллельны.
Один из признаков параллельности прямых на плоскости гласит:
1. признак. Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны.
Этот признак легко доказать, если вспомнить, что к прямой в плоскости из любой точки можно провести только один перпендикуляр.
Допустим, что прямые, перпендикулярные одной и той же прямой, не параллельны, то есть имеют общую точку.
Получается противоречие — из одной точки (H) к прямой (c) проведены два перпендикуляра. Такое невозможно, поэтому две прямые на плоскости, перпендикулярные одной и той же прямой, параллельны.
Для рассмотрения других признаков надо ознакомиться с некоторыми видами углов:
1) вспомним, что нам известны названия и свойства углов, которые образуют две пересекающиеся прямые.
Вертикальные углы равны: ∡1=∡3;∡2=∡4.
Сумма смежных углов 1800:∡1+∡2=∡2+∡3=∡3+∡4=∡4+∡1=1800.
2) Если две прямые пересекает третья прямая, то углы называются так:
накрест лежащие углы: ∡3 и ∡5;∡2 и ∡8;
соответственные углы: ∡1 и ∡5;∡4 и ∡8;∡2 и ∡6;∡3 и ∡7;
односторонние углы: ∡3и∡8;∡2и∡5.
Эти углы помогут определить параллельность прямых (a) и (b). Итак, другой признак параллельности прямых на плоскости гласит:
2. признак. Если при пересечении двух прямых третьей секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна (180°) — то прямые параллельны.
Докажем этот признак.
Сначала докажем: если прямые (a) и (b) пересекает прямая (c), и накрест лежащие углы равны, то прямые (a) и (b) параллельны.
Например, если ∡3=∡5, то a∥b.
1) Отметим точки (C) и (D), в которых прямые (a) и (b) пересекает прямая (c). Через серединную точку (K) этого отрезка проведём перпендикуляр (AB) к прямой (a).
2) ∡CKA (=) ∡DKB как вертикальные углы, ∡3 (=) ∡5 (=) α, (CK = KD) — значит, ΔCKA (=) ΔDKB по признаку о стороне и двум прилежащим к ней углам.
3) Очевидно, если ΔCKA прямоугольный, то и ΔDKB прямоугольный, и (AB) перпендикулярен к прямой (b).
4) Согласно первому доказанному признаку прямые, перпендикулярные одной и той же прямой, параллельны.
5) В случае, когда равны соответственные углы, имеем в виду, что вертикальные углы равны, и доказываем, как в пунктах 1) — 4).
6) В случае, когда сумма односторонних углов равна 180°, имеем в виду, что сумма смежных углов тоже равна (180°), и используем в доказательстве пункты 1) — 4).
3. признак. При пересечении двух параллельных прямых третьей секущей:
— накрест лежащие углы равны,
— соответственные углы равны,
— сумма односторонних углов равна (180°).
О свойствах параллельных прямых — в следующем пункте теории.
Паралле́льные прямы́е (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны.
В евклидовой геометрии[править | править код]
На чертежах параллельные линии выделяются одинаково направленными стрелками.
В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются[1].
В другом варианте определения совпадающие прямые также считаются параллельными[2][3].
Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности[4].
Параллельность прямых и обычно обозначается:
Свойства[править | править код]
- Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Соответственные углы равны (Рис.1).
- Накрест лежащие углы равны (Рис.2).
- Внутренние односторонние углы в сумме составляют 180° (Рис.3).
- Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
- Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.
Построение параллельных прямых[править | править код]
В стереометрии[править | править код]
В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
В геометрии Лобачевского[править | править код]
Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к ней
В геометрии Лобачевского в плоскости через точку вне данной прямой проходит бесконечное множество прямых, не пересекающих .
Прямая называется равнобежной прямой в направлении от к , если:
- точки и лежат по одну сторону от прямой ;
- прямая не пересекает прямую , но всякий луч, проходящий внутри угла , пересекает луч .
Аналогично определяется прямая, равнобежная в направлении от к .
Равнобежные прямые называются также асимптотически параллельными или просто параллельными.
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися[5].
Свойства[править | править код]
Расходящиеся параллельные прямые имеют единственный общий перпендикуляр.
Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.
Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.
См. также[править | править код]
- Параллельность плоскостей
- Антипараллельные прямые
- Перпендикулярность
- Ортогональность