Какие свойства можно привести для описания множества объектов
Ответы на вопросы и задания
Самое главное
Объект — это любая часть окружающей действительности (предмет, процесс, явление), воспринимаемая человеком как единое целое.
Множество — это совокупность, набор, коллекция объектов.
Каждый объект имеет имя, которое позволяет отличать его от других объектов. Имена бывают общими, обозначающими множество объектов, и единичными, обозначающими конкретный объект в некотором множестве.
В сообщении об объекте человек может описать его признаки — свойства, действия, поведение, состояние.
Вопросы и задания
1. Дайте имена объектам:
а) выросшим на грядке;
Овощи
б) проживающим в Москве;
Москвичи
в) управляющим трактором;
Трактористы
г) посещающим детский сад;
Дети из детского сада (детсадовцы)
д) находящимся в школе.
Школьники
2. Приведите примеры:
а) пустого множества;
Множество 4 ногих обезьян
б) множества, состоящего из одного элемента;
Множество хвостов собаки
в) множества, состоящего из 10 элементов;
Множество целых чисел от 1 до 10
г) бесконечного множества.
Множество натуральных чисел
3. Дайте несколько возможных общих имён каждой группе объектов. Выберите из них самое подходящее. Ответ обоснуйте:
а) Буратино, Мальвина, Пьеро, Артемон;
Персонажи сказки Буратино
б) «12 месяцев», «Морозко», «Золушка», «Синяя борода»;
Сказки
в) Москва, Санкт-Петербург, Новосибирск;
Крупные города России
г) Енисей, Волга, Лена, Москва;
Реки России
д) Москва, Санкт-Петербург, Тула.
Города России
4. Вспомните по одному объекту каждого из приведённых множеств и обозначьте его единичным именем в этом множестве:
а) мореплаватель;
Христофор Колумб
б) орфограмма;
Орфограмма безударная проверяемая гласная в корне слова.
в) формула;
Формула вычисления площади прямоугольника S=a*b
г) былина.
Былина Добрый молодец Илья Муромец
5. Назовите общие имена объектов, о которых сообщается в путеводителях. Назовите единичные имена объектов, о которых может рассказать человек после туристической поездки по России.
Страны, города, моря, достопримечательности.
Город Москва, Кремль, река Москва.
6. Каким образом можно узнать признаки интересующих вас объектов?
Изучением свойств этих объектов.
7. Какие свойства можно привести при описании множества объектов? Можно ли для множества объектов привести значения величин? Приведите примеры.
При описании объектов можно привести свойства присущие всем объектам. Значения величин можно привести если они одинаковы для множества и нельзя если значения отличаются.
Множество обезьяны, можно указать число глаз, лап. Нельзя указать вес, рост т.к. эти параметры будут индивидуальны.
8. Для каждого примера укажите объект, его свойство, определяющую свойство величину и её значение:
а) рыжеволосый человек;
Человек, рыжеволосый, цвет волос, рыжие.
б) семикилограммовый арбуз;
Арбуз, семикилограммовый, вес, 7 килограмм.
в) фарфоровая чашка;
Чашка, фарфоровая, материал, фарфор.
г) семнадцатидюймовый монитор.
Монитор, семнадцатидюймовый, размер экрана, 17 дюймов.
9. Назовите для каждого из приведённых действий два предмета, с которыми указанное действие человек выполняет по-разному: собрать;заполнить;открыть;связать;включить;сложить;измерить;поймать.
Собрать ягоды, конструктор.
Заполнить ведро, таблицу.
Открыть дверь, банку.
Связать шарф, данные.
Включить свет, компьютер.
Сложить числа, одежду.
Измерить глубину, стороны треугольника.
Поймать птицу, мышь.
10. Приведите примеры возможных активных и пассивных действий для объектов «птица», «мяч», «велосипед».
Птицы сидят на ветке. Птицы клюют зерно.
Мяч лежит на веранде. Мяч перелетел через забор.
Велосипед стоит в углу. На велосипеде едут по парку.
11. Приведите примеры пошаговых описаний действий человека. Как их называют?
Называют алгоритм. Например рецепт приготовления пирожков.
12. Ответьте на следующие вопросы.
а) Значением какой величины определяется переход чайника в состояние «кипит»?
Температура воды.
б) В каком состоянии находится вода, если её нельзя вылить из чашки?
В замороженном или испаренном.
в) В каком состоянии находится карандаш, когда с его помощью нельзя ничего написать или нарисовать?
Затупился, сломан, не заточен.
г) В каком состоянии находится долька яблока, если её можно согнуть, и она при этом не ломается?
В упругом.
Практическая работа №2
«Работаем с объектами файловой системы»
Отношения объектов
 |
|
Человек может рассказать не только о свойствах объекта, но и об отношениях, в которых этот объект находится с другими объектами.
Например:
• «Иван — сын Андрея»;
• «Эверест выше Эльбруса»;
• «Винни Пух дружит с Пятачком»;
• «21 кратно 3»;
• «Кострома такой же старинный город, как и Москва»;
• «Текстовый процессор входит в состав программного обеспечения компьютера».
В каждом из приведенных предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.
Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:
• «Дискета является носителем информации»;
• «Камчатка — это полуостров (является полуостровом)».
В каждом из этих предложений описано отношение «является элементом множества».
Отношение может связывать два множества объектов, например:
• «Колеса входят в состав автомобилей»;
• «Бабочки — это насекомые (являются разновидностью насекомых)».
Попарно связаны одним и тем же отношением могут быть несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нем трудно разобраться.
Пусть про населенные пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населенный пункт А соединен железной дорогой с населенными пунктами В, Г и Е, населенный пункт Е — с населенными пунктами В, Г и Д.
Для большей наглядности имеющиеся связи («соединен железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. (рис. 1.2).
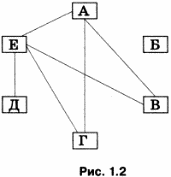
Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения обозначают стрелкой на схеме отношений.
Так, на рис. 1.3 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».
Стрелки можно не использовать, если удается сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 1.3 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.
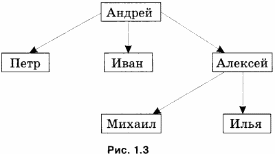
Такие отношения, как «приходится сыном», «соединен железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. А в отношениях «входит в состав» и «является разновидностью» могут находиться любые объекты.
Коротко о главном
В сообщении об объекте могут быть приведены не только свойства данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.
Любые отношения между объектами можно наглядно описать с помощью схемы отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. Связи между объектами могут быть изображены линиями или стрелками.
Вопросы и задания
1. Назовите имя отношения в каждом приведенном предложении. Какое имя можно будет дать отношению, если имена объектов в предложении поменять местами? В каких парах имя отношения при этом не изменится?
а) Колобок поет песню Лисе.
б) Конек-Горбунок помогает Ивану.
в) В Москве есть Манежная площадь.
г) Пилюлькин лечит Сиропчика.
д) Страшила путешествует вместе с Элл и.
2. Для каждой пары объектов укажите соответствующее отношение.
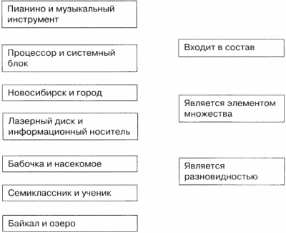
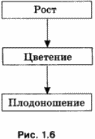
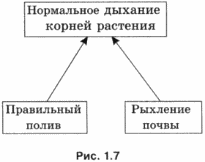
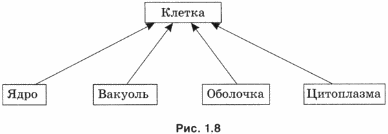
3. Какую связь отражает каждая схема отношений на рис. 1.4-1.8? Выберите правильный ответ из следующих вариантов:
• «является разновидностью»;
• «входит в состав»;
• «является условием (причиной)»;
• «предшествует».
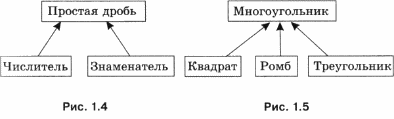
Разновидности объектов и их классификация
 |
|
Из двух множеств, связанных отношением «является разновидностью», одно является подмножеством другого. Например, множество попугаев является подмножеством множества птиц, множество натуральных чисел является подмножеством множества целых чисел.
Схему отношения «является разновидностью» мы будем называть схемой разновидностей (рис. 1.9). Такие схемы используются в учебниках, каталогах и энциклопедиях для описания самых разных объектов, например растений, животных, сложных предложений, транспортных средств и т. д.
На схеме разновидностей имя подмножества всегда располагается ниже имени включающего его множества.
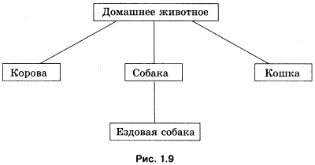
Объекты подмножества обязательно обладают всеми признаками объектов множества (наследуют признаки множества) и кроме них имеют еще свой, дополнительный признак (или несколько признаков). Этим дополнительным признаком может быть свойство или действие. Например, любое домашнее животное нужно кормить, собаки, кроме того, лают и кусаются, а ездовые собаки, кроме того, еще и бегают в упряжке.
Важно понимать, что сами по себе объекты не делятся ни на какие множества и подмножества. Например, арбузу совершенно «безразлично», относят его к семейству тыквенных растений, к подмножеству полосатых или шарообразных объектов. Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5-9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, еще раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются основанием классификации.
Классификация называется естественной, если в качестве ее основания взяты существенные признаки объектов. Примером естественной классификации является классификация живых существ, предложенная Карлом Линнеем (1735 г.). В настоящее время ученые разделяют множество всех живых существ на пять основных царств: растения, грибы, животные, простейшие и прокариоты. Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.
Классификация называется искусственной, если в качестве ее основания взяты несущественные признаки объектов. К
искусственным классификациям относятся вспомогательные классификации (алфавитно-предметные указатели, именные каталоги в библиотеках).
Пример искусственной классификации — деление множества звезд на небе на созвездия, проводившееся по признакам, которые к самим звездам не имели никакого отношения.
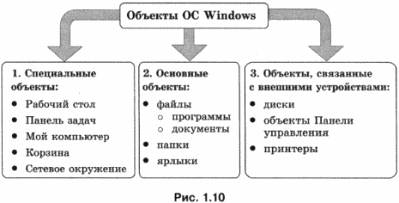
Можно предложить следующую классификацию объектов, с которыми взаимодействует пользователь в операционной системе Windows (рис. 1.10).
Коротко о главном
Схема разновидностей — это схема отношений «является разновидностью» между множествами и подмножествами объектов.
У объектов подмножества есть дополнительные признаки, кроме тех, которые есть у объектов множества, включающего данное подмножество.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются осно¬ванием классификации.
Вопросы и задания
1. Для каждого из указанных подмножеств назовите множество, с которым оно связано отношением «является разновидностью» (назовите общее имя, отвечающее на вопрос «Что это такое?»):
а) местоимение;
б) запятая;
в) джойстик;
г) параллелограмм;
д) ратуша;
е) басня;
ж) капилляр.
2. Найдите в списке шесть пар множеств, между которыми существуют отношения «является разновидностью». Определите в каждой такой паре имя подмножества. Назовите для него хотя бы одно дополнительное свойство:
• книга;
• бензин;
• врач;
• молоко;
• строитель;
• учебник;
• жидкость;
• справочник;
• человек.
3. Выберите из списка имена девяти множеств, связанных отношениями «является разновидностью». Составьте схему разновидностей:
• яблоня;
• хвойное дерево;
• сосна;
• пихта;
• дерево;
• лиственное дерево;
• яблоко;
• ствол;
• фруктовое дерево;
• береза;
• дуб;
• лиственница;
• корень;
• желудь.
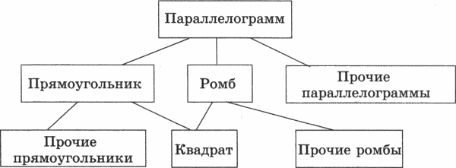
4. Используя предложенную классификацию паралле-лограммов, опишите свойства квадрата, наследующего их сразу у двух предков — прямоугольника и ромба. Какими дополнительными свойствами обладает квадрат:
а) по отношению к прямоугольнику;
б) по отношению к ромбу?
5. В каждом пункте перечислены объекты, сгруппированные по классам. Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
а) ель, сосна, кедр, пихта / береза, осина, липа, тополь;
б) картофель, лук, огурцы, помидоры / яблоки, апельсины, груши, мандарины;
в) рожь, тишь, ложь, рысь / пшеница, тишина, истина, кошка;
г) рубашка, пиджак, платье, сарафан / пальто, шуба, плащ, штормовка;
д) волк, медведь, лиса, лось / корова, собака, кошка, лошадь.
6. Предложите свою классификацию компьютерных объектов «файл» и «документ».
Практическая работа №2
«Работаем с объектами файловой системы»
1. Откройте окно Мой компьютер. Просмотрите файлы и папки, расположенные на диске С:.
2. Воспользуйтесь кнопками Вперед и Назад на панели инструментов Обычные кнопки для перемещения между ранее просмотренными объектами.

3. Выберите в меню Вид команды: Эскизы страниц, Плитка, Значки, Таблица. Проследите за изменениями в отображении папок и файлов.
Найдите на панели инструментов Обычные кнопки кнопку, обеспечивающую быстрое изменение вида содержимого папок.
4. С помощью кнопки Папки отобразите в левой части окна панель Обозревателя Папки. С ее помощью еще раз просмотрите файлы и папки, расположенные на диске С:. Проследите за изменениями, происходящими в правой части окна.
5. С помощью кнопки Поиск найдите собственную папку — папку, в которой хранятся ваши работы. Для этого в окне Помощника по поиску щелкните на ссылке Файлы и папки. В соответствующих полях укажите имя папки и область поиска.
6. Откройте собственную папку. В ней должны быть вложенные папки Документы, Заготовки_6, Заготовки_7, Презентации и Рисунки. Просмотрите содержимое этих папок.
7. Папка Заготовки_6 содержит файлы, которыми вы пользовались при выполнении работ компьютерного практикума в пошлом году. Так как эта папка вам больше не нужна, удалите ее (например, командой контекстного меню).
8. Папки Документы, Презентации и Рисунки содержат ваши прошлогодние работы. Их хотелось бы сохранить.
Создайте в собственной папке папку Архив. Для этого переведите указатель мыши в чистую область окна собственной папки и щелкните правой кнопкой мыши (вызов контекстного меню). Выполните команду [Создать-Папку].
Поочередно переместите папки Документы, Презентации и Рисунки в папку Архив. Для этого:
1) выделите папку Документы и, удерживая нажатой левую кнопку мыши, перетащите папку Документы в нанку Архив;
2) откройте контекстное меню панки Презентации, выполните команду Вырезать. Откройте папку Архив и с помощью контекстного меню вставьте в нее папку Презентации;
3) вырежьте папку Рисунки и вставьте ее в папку Архив с помощью команд строки меню.
9. С помощью контекстного меню переименуйте папку Заготовки_7 в Заготовки.
10. Убедитесь, что ваша папка имеет структуру, аналогичную приведенной ниже:

11. Откройте файл Описание.doc из папки Заготовки.
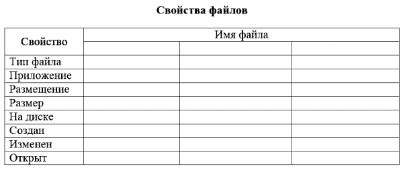
Внесите в соответствующие ячейки таблицы информацию о свойствах трех своих файлов — текстового документа, рисунка и презентации.
12. Сохраните файл в собственной папке под именем Описание1. Вспомните как можно больше способов завершения работы с программой. Завершите работу с программой.
Теперь мы умеем
— выполнять операции с объектами файловой системы — папками и файлами;
— определять свойства объектов файловой системы.

Множество – определенная совокупность объектов.
Объекты, из которых состоит множество, называются элементами множества.
ПРИМЕР
Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
Множества обычно обозначают заглавными латинскими буквами А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c, d, x, y…
Для обозначения того, что объект x является элементом множества A, используют символику: xА (читается: x принадлежит А ), запись xА обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).
Множество не содержащее ни одного элемента называется пустым (обозначается: Ø).
Множества из элементов которого составляем конкретное множество называется универсальным (обозначается: U).
ПРИМЕР
U – множество людей на земле, А – студенты группы Эп-305.
Множества можно изображать с помощью кругов, которые называются кругами Эйлера или диаграммами Венна, универсальное множество принято обозначать прямоугольником.
ПРИМЕР

Тема 2.2. Способы задания множеств
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
1) Перечислением всех элементов множества в фигурных скобках.
ПРИМЕР
A = {Оля, Маша, Саша}
2) Характеристическим предикатом, который описывает свойство всех элементов, входящих в множество. Характеристический предикат записывается после двоеточия или символа « | ».
ПРИМЕР
Р(x) = xN x < 8 — характеристический предикат.
M = {x : Р(x)} или M = {x : xN x < 8}.
Множество M можно задать и перечислением его элементов:
M = {1, 2, 3, 4, 5, 6, 7}
ПРИМЕР
В = {x | x — четное натуральное число} = {2, 4, 6, 8, …}
Если множество состоит из небольшого количества элементов, то его удобно задавать перечислением всех элементов, если же элементов много или множество имеет бесконечное число элементов, то оно задается с помощью характеристического предиката.
Тема 2.3. Операции над множествами
1) Сравнение множеств
Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.
Два множества называются равными, если они содержат одинаковые наборы элементов.
ТЕОРЕМА
# Пустое множество Ø является подмножеством всех множеств.
# Универсальное множество U содержит все множества.
# Если , то В надмножество А.
ПРИМЕР
А={0, 1, 2, 3}, В={0, 1}, .

2) Объединением двух множеств называется множество, содержащее все элементы обоих множеств.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я},
.

3) Пересечением двух множеств называется множество, состоящее из общих элементов обоих множеств.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, ={К, Т, Я}.

4) Разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, А В={A}, В А ={О, С}.


5) Симметрической разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В и всех элементов множества В не содержащихся в А.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, А Δ В={A,О,С}.

6) Дополнением (дополнением до универсального множества) множества А называется множество, состоящее из всех элементов универсального множества не содержащихся в А.

7) Прямым или декартовым произведением множеств A и B, называется множество всех упорядоченных пар (a, b), где первый элемент a из множества A, а второй элемент b из множестваB.
ПРИМЕР
,
Степенью множества называется декартовое произведение множества A само на себя n раз.
ПРИМЕР
, .
Свойства операций над множествами
1) Коммутативность.
2) Ассоциативность.
3) Дистрибутивность.
4) Закон поглощения.
5) Идемпотентность.
6) Инволютивность.
7) Свойство нуля.
АØ=А
АØ= Ø
8) Свойство единицы.
9) Закон де Моргана
Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается: | X |
ПРИМЕР
X ={1,3,6},
| X | = 3
6

