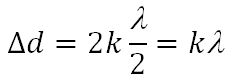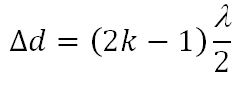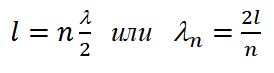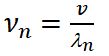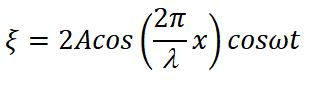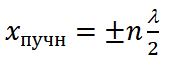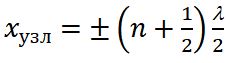Какие свойства механических волн
С волнами любого происхождения при определённых условиях можно наблюдать четыре ниже перечисленных явления, которые мы рассмотрим на примере звуковых волн в воздухе и волн на поверхности воды.
Отражение волн. Проделаем опыт с генератором тока звуковой частоты, к которому подключён громкоговоритель (динамик), как показано на рис. «а». Мы услышим свистящий звук. На другом конце стола поставим микрофон, соединённый с осциллографом. Поскольку на экране возникает синусоида с малой амплитудой, значит, микрофон воспринимает слабый звук.
Расположим теперь сверху над столом доску, как показано на рис.«б». Поскольку амплитуда на экране осциллографа возросла, значит, звук, доходящий до микрофона, стал громче. Этот и многие другие опыты позволяют утверждать, что механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред.
Преломление волн. Обратимся к рисунку, где изображены волны, набегающие на прибрежную мель (вид сверху). Серо-жёлтым цветом изображён песчаный берег, а голубым – глубокая часть моря. Между ними есть песчаная мель – мелководье.
Волны, бегущие по глубокой воде, распространяются в направлении красной стрелки. В месте набегания на мель волна преломляется, то есть изменяет направление распространения. Поэтому синяя стрелка, указывающая новое направление распространения волны, расположена иначе.
Это и многие другие наблюдения показывают, что механические волны любого происхождения могут преломляться при изменении условий распространения, например, на границе раздела двух сред.
Дифракция волн. В переводе с латинского «дифрактус» означает «разломанный». В физике дифракцией называется отклонение волн от прямолинейного распространения в одной и той же среде, приводящее к огибанию ими препятствий.
Взгляните теперь на другой рисунок волн на поверхности моря (вид с берега). Волны, бегущие к нам издалека, заслоняются большой скалой слева, но при этом частично огибают её. Скала меньших размеров справа и вовсе не является преградой для волн: они полностью её огибают, распространяясь в прежнем направлении.
Опыты показывают, что дифракция наиболее отчётливо проявляется, если длина набегающей волны больше размеров препятствия. Позади него волна распространяется так, как будто препятствия не было.
Интерференция волн. Мы рассмотрели явления, связанные с распространением одной волны: отражение, преломление и дифракцию. Рассмотрим теперь распространение с наложением друг на друга двух или более волн – явление интерференции (от лат. «интер» – взаимно и «ферио» – ударяю). Изучим это явление на опыте.
К генератору тока звуковой частоты присоединим два динамика, соединённые параллельно. Приёмником звука, как и в первом опыте, будет микрофон, подключённый к осциллографу.
Начнём двигать микрофон вправо. Осциллограф покажет, что звук становится то слабее, то сильнее, несмотря на то, что микрофон удаляется от динамиков. Вернём микрофон на среднюю линию между динамиками, а затем будем двигать его влево, снова удаляя от динамиков. Осциллограф вновь покажет нам то ослабление, то усиление звука.
Этот и многие другие опыты показывают, что в пространстве, где распространяются несколько волн, их интерференция может приводить к возникновению чередующихся областей с усилением и ослаблением колебаний.
Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.
Определение 1
Волна – это процесс распространения колебаний в среде.
Виды механических волн
Различают следующие виды механических волн:
Определение 2
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.
Пример: волны, распространяющиеся по струне или резиновому жгуту в натяжении (рисунок 2.6.1);
Определение 3
Продольная волна: частицы среды смещаются в направлении распространения механической волны.
Пример: волны, распространяющиеся в газе или упругом стержне (рисунок 2.6.2).
Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.
Замечание 1
Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.
Рисунок 2.6.1. Распространение поперечной волны по резиновому жгуту в натяжении.
Рисунок 2.6.2. Распространение продольной волны по упругому стержню.
Модель твердого тела
Характерная черта механических волн – их распространение в материальных средах в отличие, например, от световых волн, способных распространяться и в пустоте. Для возникновения механического волнового импульса необходима среда, имеющая возможность запасать кинетическую и потенциальную энергии: т.е. среда должна иметь инертные и упругие свойства. В реальных средах эти свойства получают распределение по всему объему. К примеру, каждому небольшому элементу твердого тела присуща масса и упругость. Самая простая одномерная модель такого тела представляет из себя совокупность шариков и пружинок (рисунок 2.6.3).
Рисунок 2.6.3. Простейшая одномерная модель твердого тела.
В этой модели инертные и упругие свойства разделены. Шарики имеют массу m, а пружинки – жесткость k. Такая простая модель дает возможность описать распространение продольных и поперечных механических волн в твердом теле. При распространении продольной волны шарики смещаются вдоль цепочки, а пружинки растягиваются или сжимаются, что есть деформация растяжения или сжатия. Если подобная деформация происходит в жидкой или газообразной среде, ее сопровождает уплотнение или разрежение.
Замечание 2
Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.
Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.
В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.
Замечание 3
Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.
В плане практического применения особый интерес представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны получают распространение в однородных средах с некоторой постоянной скоростью υ.
Запишем выражение, показывающее зависимость смещения y(x, t) частиц среды из положения равновесия в синусоидальной волне от координаты x на оси OX, вдоль которой распространяется волна, и от времени t:
y(x, t)=Acos ωt-xυ=Acos ωt-kx.
В приведенном выражении k=ωυ – так называемое волновое число, а ω=2πf является круговой частотой.
Бегущая волна
Рисунок 2.6.4 демонстрирует «моментальные фотографии» поперечной волны в момент времени t и t+Δt. За промежуток времени Δt волна перемещается вдоль оси OX на расстояние υΔt. Подобные волны носят название бегущих волн.
Рисунок 2.6.4. «Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t+Δt.
Определение 4
Длина волны λ – это расстояние между двумя соседними точками на оси OX, испытывающими колебание в одинаковых фазах.
Расстояние, величина которого есть длина волны λ, волна проходит за период Т. Таким образом, формула длины волны имеет вид: λ=υT, где υ является скоростью распространения волны.
С течением времени t происходит изменение координатыx любой точки на графике, отображающем волновой процесс (к примеру, точка А на рисунке 2.6.4), при этом значение выражения ωt–kx остается неизменным. Спустя время Δt точка А переместится по оси OX на некоторое расстояние Δx=υΔt. Таким образом:
ωt-kx=ω(t+∆t)-k(x+∆x)=const или ω∆t=k∆x.
Из указанного выражения следует:
υ=∆x∆t=ωk или k=2πλ=ωυ.
Становится очевидно, что бегущая синусоидальная волна имеет двойную периодичность – во времени и пространстве. Временной период является равным периоду колебаний T частиц среды, а пространственный период равен длине волны λ.
Определение 5
Волновое число k=2πλ – это пространственный аналог круговой частоты ω=-2πT.
Сделаем акцент на том, что уравнение y(x,t)=Acos ωt+kx является описанием синусоидальной волны, получающей распространение в направлении, противоположном направлению оси OX, со скоростью υ=-ωk.
Когда бегущая волна получает распространение, все частицы среды гармонически колеблются с некоторой частотой ω. Это означает, что как и при простом колебательном процессе, средняя потенциальная энергия, являющаяся запасом некоторого объема среды, есть средняя кинетическая энергия в том же объеме, пропорциональная квадрату амплитуды колебаний.
Замечание 4
Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляетсяпоток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Скорость распространения волны
Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.
Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы μ (или массы единицы длины) и силы натяжения T:
υ=Tμ.
Скорость, с которой продольные волны распространяются в безграничной среде, рассчитывается при участии таких величин как плотность среды ρ (или масса единицы объема) и модульвсестороннего сжатия B (равен коэффициенту пропорциональности между изменением давления Δp и относительным изменением объема ΔVV, взятому с обратным знаком):
∆p=-B∆VV.
Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:
υ=Bρ.
Пример 1
При температуре 20 °С скорость распространения продольных волн в воде υ≈1480 м/с, в различных сортах стали υ≈5–6 км/с.
Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:
υ=Eρ.
Для стали отличие E от B незначительно, а вот для прочих материалов оно может составлять 20–30 % и больше.
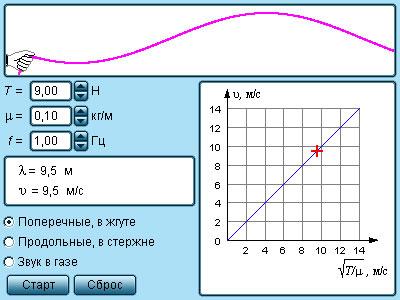
Рисунок 2.6.5. Модель продольных и поперечных волн.
Стоячая волна
Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.
Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.
Допустим, струна длины l зафиксирована таким образом, что один из ее концов расположен в точке x=0, а другой – в точке x1=L (рисунок 2.6.6). В струне имеется натяжение T.
Рисунок 2.6.6. Возникновение стоячей волны в струне, зафиксированной на обоих концах.
По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:
- y1(x, t)=A cos (ωt+kx) – волна, распространяющаяся справа налево;
- y2(x, t)=A cos (ωt-kx) – волна, распространяющаяся слева направо.
Точка x=0 — один из зафиксированных концов струны: в этой точке падающая волна y1 в результате отражения создает волну y2. Отражаясь от зафиксированного конца, отраженная волна входит в противофазу с падающей. В соответствии с принципом суперпозиции (что есть экспериментальный факт) колебания, созданные встречными волнами во всех точках струны, суммируются. Из сказанного следует, что итоговое колебание в каждой точке определяется как сумма колебаний, вызванных волнами y1 и y2 в отдельности. Таким образом:
y=y1(x, t)+y2(x, t)=(-2A sin ωt) sin kx.
Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.
Определение 6
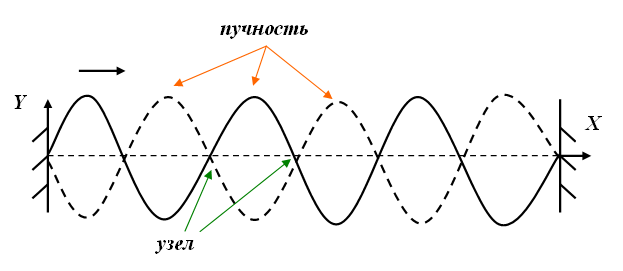
Узлы – точки неподвижности в стоячей волне.
Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.
Если следовать данным определениям, для возникновения стоячей волны оба зафиксированных конца струны должны являться узлами. Указанная ранее формула отвечает этому условию на левом конце (x=0). Чтобы условие было выполнено и на правом конце (x=L), необходимо чтобы kL=nπ, где n является любым целым числом. Из сказанного можно сделать вывод, что стоячая волна в струне появляется не всегда, а только тогда, когда длина L струны равна целому числу длин полуволн:
l=nλn2 или λn=2ln(n=1, 2, 3,…).
Набору значений λn длин волн соответствует набор возможных частот f
fn=υλn=nυ2l=nf1.
В этой записи υ=Tμ есть скорость, с которой распространяются поперечные волны по струне.
Определение 7
Каждая из частот fn и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f1 носит название основной частоты, все прочие (f2, f3, …) называются гармониками.
Рисунок 2.6.6 иллюстрирует нормальную моду для n=2.
Стоячая волна не обладает потоком энергии. Энергия колебаний, «запертая» в отрезке струны между двумя соседними узлами, не переносится в остальные части струны. В каждом таком отрезке происходит периодическое (дважды за период T) преобразование кинетической энергии в потенциальную и обратно, подобно обычной колебательной системе. Однако, здесь имеется различие: если груз на пружине или маятник имеют единственную собственную частоту f0=ω02π, то струна характеризуется наличием бесконечного числа собственных (резонансных) частот fn. На рисунке 2.6.7 показано несколько вариантов стоячих волн в струне, зафиксированной на обоих концах.
Рисунок 2.6.7. Первые пять нормальных мод колебаний струны, зафиксированной на обоих концах.
Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями n) способны одновременно присутствовать в колебаниях струны.
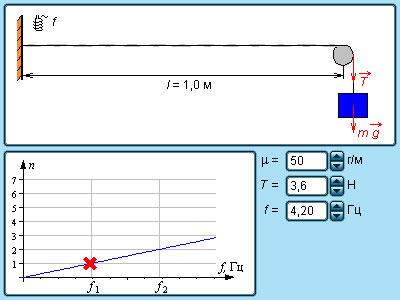
Рисунок 2.6.8. Модель нормальных мод струны.
Волна — это процесс распространения колебания в среде с течением времени
Для существования волны необходим источник колебания и материальная среда или поле, в которых эта волна распространяется. Волны бывают самой разнообразной природы, но они подчиняются аналогичным закономерностям.
По физической природе различают:
Механические волны упругие, звуковые, волны на поверхности жидкости
| Электромагнитные волны свет, радиоволны, излучения |
По ориентации возмущений различают:
Продольные волны — Смещение частиц происходит вдоль направления распространения; могут распростаняться только в упругих средах; необходимо наличие в среде силы упругости при сжатии; могут распространяться в любых средах. Примеры:звуковые волны
| Поперечные волны — Смещение частиц происходит поперек направления распространения; могут распростаняться только в упругих средах; необходимо наличие в среде силы упругости при сдвиге; могут распространяться только в твердых средах (и на границе двух сред). Примеры: упругие волны в струне, волны на воде |
По характеру зависимости от времени различают:
Упругие волны — механические возмещения (деформации), распространяющиеся в упругой среде. Упругая волна называется гармонической (синусоидальной), если соответствующие ей колебания среды являются гармоническими.
Бегущие волны — волны, переносящие энергию в пространстве.
По форме волновой поверхности: плоская, сферическая, цилиндрическая волна.
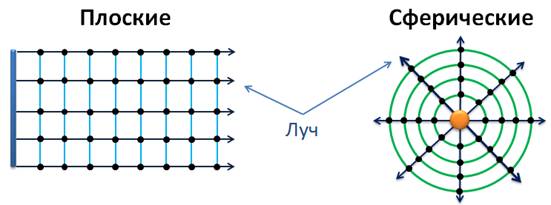
Волновой фронт — геометрическое место точек, до которых дошли колебания к данному моменту времени.
Волновая поверхность — геометрическое место точек, колеблющихся в одной фазе.
Характеристики волны
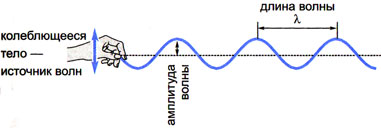
Длина волны λ — расстояние, на которое волна распространяется за время, равное периоду колебаний
Амплитуда волны А — амплитуда колебаний частиц в волне
Скорость волны v — скорость распространения возмущений в среде
Период волны Т — период колебаний
Частота волны ν — величина, обратная периоду
Уравнение бегущей волны
В процессе распространения бегущей волны возмущения среды доходят до следующих точек пространства, при этом волна переносит энергию и импульс, но не переносит вещество (частицы среды продолжают колебаться в том же месте пространства).
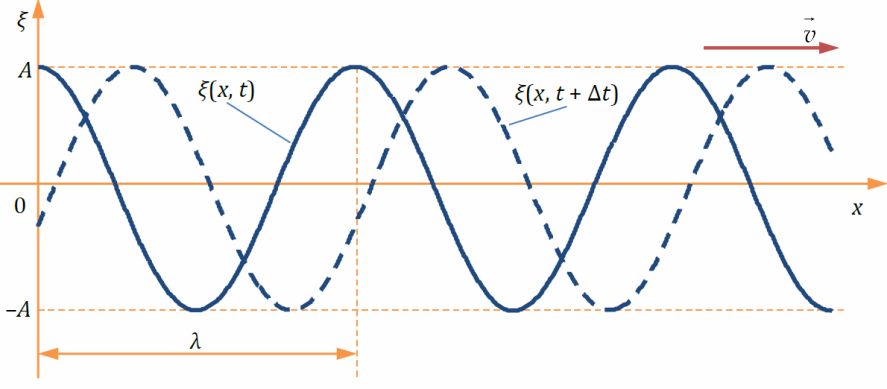
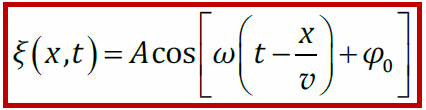
где v – скорость, φ0 – начальная фаза, ω – циклическая частота, A – амплитуда
Свойства механических волн
1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.
2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.
3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.
4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний
Интерференция и дифракция механических волн.
Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении.
При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн.
Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.
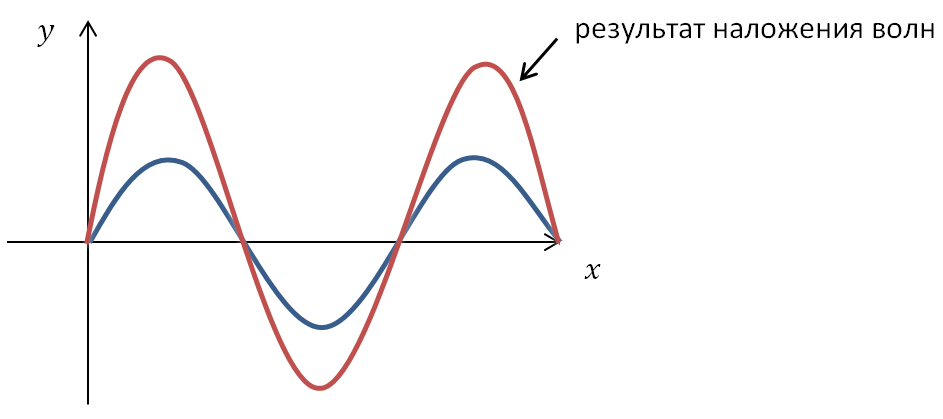
Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.
Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.
Условия максимума и минимума
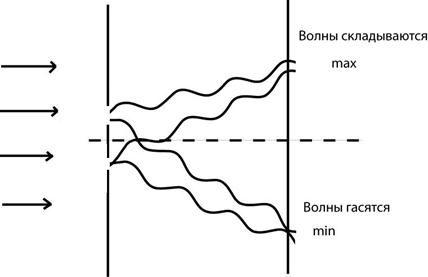
Если колебания точек А и Б совпадают по фазе и имеют равные амплитуды, то очевидно, что результирующее смещение в точке С зависит от разности хода двух волн.
Условия максимума

Если разность хода этих волн равна целому числу волн (т. е. четному числу полуволн) Δd = kλ, где k = 0, 1, 2, …, то в точке наложения этих волн образуется интерференционный максимум.
Условие максимума:
Амплитуда результирующего колебания А = 2×0.
Условие минимума
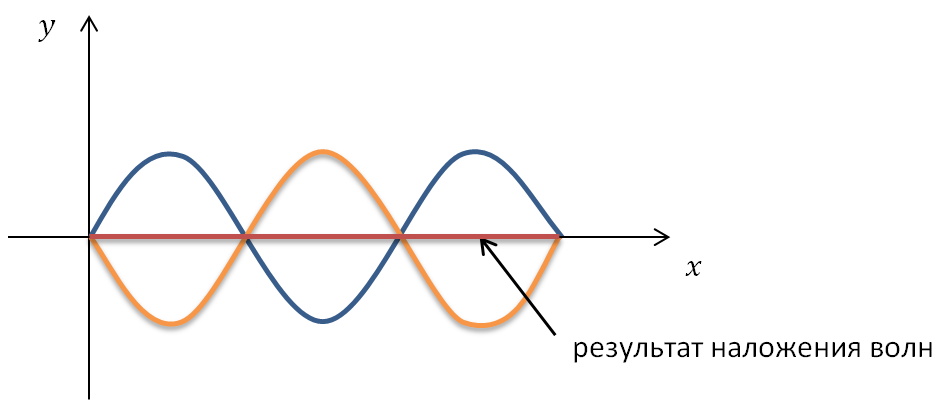
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.
Условие минимума:
Амплитуда результирующего колебания А = 0.
Если Δd не равно целому числу полуволн, то 0 < А < 2х0.
Дифракция волн.
Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией.
Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d<<λ, где d – размер препятствия.
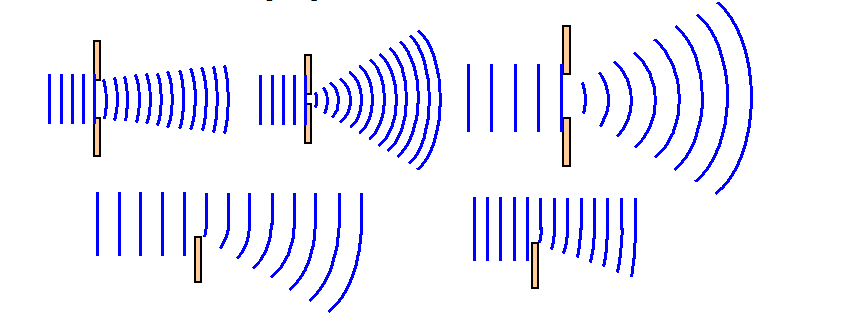
Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные.
Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.
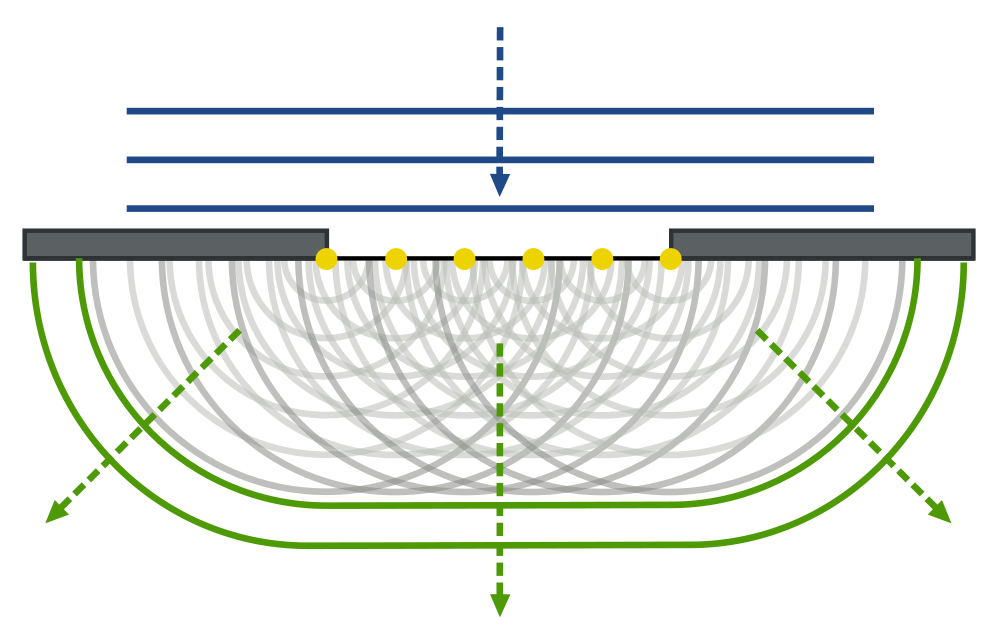
Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.
Стоячие волны
Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда.
В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Колебания струны. В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.
Отсюда вытекает условие
Длинам волн соответствуют частоты
n = 1, 2, 3…Частоты vn называются собственными частотами струны.
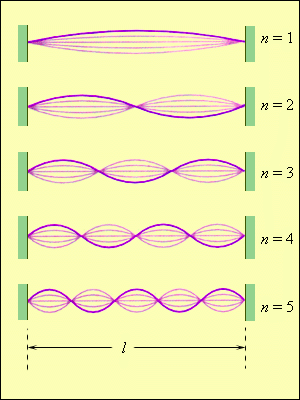
Гармонические колебания с частотами vn называются собственными или нормальными колебаниями. Их называют также гармониками. В общем случае колебание струны представляет собой наложение различных гармоник.
Уравнение стоячей волны:
В точках, где координаты удовлетворяют условию 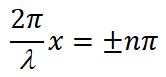
В точках, координаты которых удовлетворяют условию 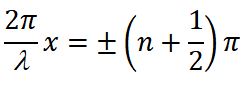
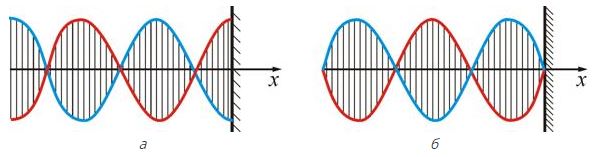
Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (a), и узел – если более плотная (б).
Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.