Какие свойства этих фигур вам известны

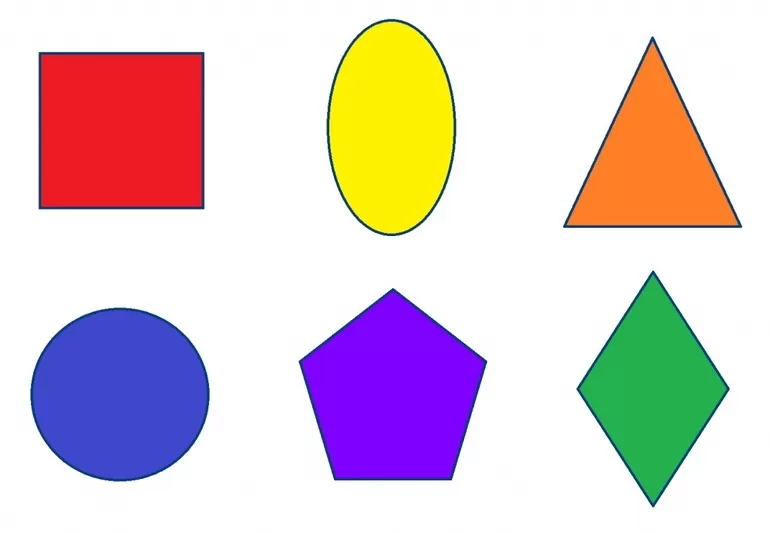
Общая характеристика
Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.
Основные понятия о составляющих
Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).
Виды линий:

- Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
- Разомкнутая. Начало и окончание не соединяются.
- Прямая. Обозначается буквой а или b.
- Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
- Кривая.Отличная от прямой линии.
Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.
Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.
Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объекты
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.
Виды треугольника в зависимости от угла (У):
- Прямой. Один У будет прямым, два — менее 90 градусов.
- Острый. Градусная мера больше 0, но меньше 90 гр.
- Тупой. Один У тупой, два других будут острыми.

Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.
Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.
Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.
Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
Сложные модели
В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.
Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.
Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).
Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.
В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.
Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.
Объемные фигуры:
- Шар.
- Конус.
- Параллелепипед.
- Цилиндр.
- Сфера.
Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.
Виды многогранников:
- Тетраэдер (четырехгранник). Это правильный треугольник.
- Куб (гексаэдр). Грани являются квадратом.
- Октаэдр. Имеется шесть вершин и восемь граней.
- Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
- Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.
В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.
Познавательные игрушки детям
Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.
Основной материал для обучения детей:
- Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
- Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
- Специальная детская литература.
Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.
Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.
Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.
Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.
Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.
Александр А. · 18 мая 2019
6,9 K
Копирайтер, увлекаюсь психологией и философией. Люблю искусство и моду
Фигуры на плоскости изучают раздел геометрии- планиметрия. Геометрическая фигура-это любое множество точек.
Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.
Основные свойства простых фигур выражаются в аксиомах:
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Эта аксиома выражает основное свойство принадлежности точек и прямых на плоскости.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
Этой аксиомой выражается основное свойство расположения точек на прямой.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Очевидно, что аксиома 3 выражает основное свойство измерения отрезков.
- Прямая разбивает плоскость на две полуплоскости.
Этим предложением выражается основное свойство расположения точек относительно прямой на плоскости.
Какие вопросы изучает геометрия?
Дорога под названием «потом» ведет в страну под названием «никуда»…
Геометрия изучает форму предметов, определяет их размеры и взаимное расположение.
Наука геометрия делится на два больших раздела — планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.
Прочитать ещё 1 ответ
В какой геометрии параллельные прямые пересекаются?
Здравствуйте . Не силён в геометрии и математике, но меня всегда смущало выражение » две параллельные прямые не пересекаются». Я считаю что зависит от обстоятельств . Например если проделать опыт : два столба стоят паралельно друг другу . Если их продолжить в обе стороны до бесконечности они ни когда не пересекутся , при условии что я стою и смотрю на них . Если взять эти же 2 столба которые стоят паралельно и отойти в сторону, грубо говоря встать паралельно им и посмотреть на них ( зная что они параллельные и что их 2 ), я увижу один столб и с моей точки зрения в данном положении оба этих параллельных столба пересекаются в любой точке . То есть с точки зрения наблюдателя находящегося паралельно 2 параллельным прямым параллельные прямые пересекаются.
Понимаю что это выглядит обсурдно и наверное даже смешно , но захотелось поделиться рассуждением на эту тему )))). Грубо говоря если взять во внимание перемещение точки наблюдения во времени и пространстве то параллельные прямые пересекаются ).
Прочитать ещё 3 ответа
Как определить геометрическую форму молекулы?
Подготовила к ЕГЭ по химии 5000 учеников. С любого уровня до 100 в режиме онлайн 🙂 · vk.com/mendo_him
????sp гибридизация- это когда атомы находятся на одной линии
????sp 3 гибридизация — это когда атомы находятся в углах тетраэдра
????sp2 гибридизация-это когда атомы располагаются в одной плоскости треугольником
Есть ли обратная сторона у плоских фигур?
Плоскость, как понятие математики, и геометрии, в частности, является абстракцией. То есть, не существует на самом деле. К тому же, априори (то есть, без опыта), принимается, что плоскость не имеет толщины.
Может ли иметь обратную сторону то, что является вымыслом и не имеет толщины?
С точки зрения здравого смысла, этот вопрос лишён всякого смысла.
Но, обратную сторону плоскости, можно использоавть в художественной литературе, и разглядывать, что там с другой её сторны)
Этой статьей начинаем с Вами изучение одного из самых сложных и запутанных, но одновременно прекрасных, выверенных, наглядных и точных направлений математики — общей топологии. Название — не игра слов, к концу этой заметки Вы поймете, как математика относится ко всему роду homo sapiens. Начинаем!
Это так называемая бутылка Клейна — не правда ли завораживает? Какими свойствами обладает это фигура, можно ли ее построить в нашем трехмерном мире, как пройти из одной точки бутылки Клейна в другую?
Тополо́гия (от др. греч τόπος — место и λόγος — слово, учение) — наука, изучающая качественные свойства фигур не только в привычном нам трехмерном мире, но и в мирах с большим и меньшим количеством измерений (уж поверьте все вы сталкивались с ними, только может быть не догадывались).
Самый простой пример пространства меньшей размерности — это плоскость у которой размерность равна 2, подобно тому, как у прямоугольника есть ширина и длина.
Проделаем такой эксперимент: возьмем на плоскости квадрат и начнем его сжимать по краям, как бы сглаживая углы. После некоторого количества движений и выравниваний мы сможем получить круг — другую геометрическую фигуру. Процесс обратим — из этого круга мы всё так же можем получить квадрат. Значит ли это, что квадрат равен кругу, а круг квадрату? Конечно нет, но обычный человек сказал бы: «Они подобны», а тополог скажет: «Они гомеоморфны или получены гомеоморфным преобразованием».
Стрелки — направление растягивания.
Страшное слово? Как бы не так! Каждый из Вас (во всяком случае женская половина моей аудитории)за свою жизнь проводил гомеоморфные преобразования: «отщипнул тесто — сделал из него шар — раскатал в блин».
Гомеоморфное преобразование — это ни что иное, как растягивание или сжатие точек какой-либо фигуры без образования разрывов и склеек одинаковых точек. Возьмите раскатанный блин и порвите его по центру — получите негомеоморфное преообразование.
Возникает резонный вопрос, а какие свойства остаются неизменными при гомеоморфизме? Математики называют такие свойства качественными или топологическими и если мы хотим говорить о них, то должны как-то охарактеризовать эти свойства, хотя бы интуитивно-наглядно. Очередной эксперимент:
Возьмем сферу — поверхность точек, равноудаленную от другой точки, называемой центром сферы. Сфера — пуста, если наполнить сферу любым веществом (в нашем случае мягким и эластичным) получится шар. Попытаемся понять, чем «топологически» отличается сфера от шара?
1) Зададимся вопросом: как наикратчайшим образом добраться из одной точки сферы в другую, противоположную ей (например. с северного на южный полюс)? Правильно, пойти как нормальный человек по поверхности. А для шара? Теоретически мы могли бы «срезать» добрую часть путь проникнув через его центр и прошив его насквозь. Есть отличие!
Напоминаю, что по «пустоте» мы не перемещаемся, а внутри шара — пустота.
2) Представьте, что вы решили прокатить по поверхности сферы колесо и вернуться в ту же точку. Изменится ли направление его вращения после Вашего с ним кругосветного приключения? Очевидно и для сферы и для шара, что нет.
Именно поэтому у кругосветных путешественников-автомобилистов колеса по приезду в родной город не крутятся в одну сторону
Но есть фигуры, прокатив колесо по которым и вернувшись в ту же точку мы изменим направление его вращения! Пример — широко известный лист Мёбиуса.
Источник: https://ds04.infourok.ru/uploads/ex/01a0/001892af-c470c37a/1/hello_html_m1ce4bf27.jpg
Это свойство фигур называется ориентируемость. Шар и сфера — ориентируем, а вот лист Мёбиуса — нет. Здесь отличий между шаром и сферой не выявлено.
3) Из определения следует, что под поверхностью сферы пустота. В шаре такого нет, он заполнен полностью.
Именно в третьем различии вся «соль». Что же из него следует?
Представьте, что Вы взяли комок мокрого снега и хотите придать ему идеальную форму.
Снег еще рыхлый, поэтому сжимая снег со всех сторон Вы начнете «стягивать» точки этого шара к одной из его точек — центру.
А теперь попробуйте стянуть футбольный мяч хотя бы к одной его точке. Попробуем стянуть северный (N) и южный полюса (S). Суть в том, что в предельном приближении мяч порвется в точках W и E, а разрыв, как мы помним из определения, недопустим при гомеоморфизме.
Таким образом, мы не смогли гомеоморфно стянуть сферу к какой-либо из своих точек (зато сферу мы можем вывернуть наизнанку — видео в конце статьи), а шар смогли. В этом и заключается топологическое различие между этими фигурами: шар не гомеоморфен сфере. Остается открытым вопрос: чему же тогда гомеоморфен шар и сфера? Ответ: кубу.
Источник: https://ruread.net/bookimages/45203/img_41.jpg
Со сферой всё намного интереснее. Топологи различают сферу без ручки (тогда это просто сфера) и сферу с n-ручками, где n=1,2… Например, сфера с ручкой получается с помощью гомеоморфных преобразований из тора (бублика).
Так выглядит ручка — как подрезанный бублик.
Источник: https://habr.habrastorage.org/post_images/539/bb8/785/539bb878571fb370ff85bc9c70f4e8af.gif
Что же общего у кружки и тора? Ответ: количество дырок, и это ключевое топологическое свойство фигур. Фигуры с разным количеством дырок не могу быть гомеоморфны другу другу, не могут быть получены друг из друга посредством сжатия/растягивания. И это главный вывод нашего вводного экскурса. Где-то мог ошибиться, я думаю, найдутся корифеи. которые исправят в комментариях.
Стой, стой, а что же с человеком, который — шар с ручками?
Ах да, знакомьтесь — это человек-Шар и он попал в передрягу: у него руки закреплены между собой как два кольца.
Ему нужно помочь распутать руки не разрывая пальцы. Вы скажете невозможно, топологи скажут: элементарно.
Обещанное видео про выворачивание сферы наизнанку (завораживает):
Часть 1
Часть 2
Подведем итог:
1) Топология изучает качественные свойства геометрических фигур.
2) Топология не нарушается при гомеоморфном преобразовании: сжатии, растягивании или склейке.
3) Важнейшим топологическим свойством фигур является количество дырок.
4) Фигуры с разным количеством дырок не гомеоморфны.
На этом ознакомительная статья подходит к концу, но приступать к изучению топологии не на интуитивно-бытовом уровне еще рано. Необходимо дать и другие основополагающие понятия. а именно множества и расстояния. Этим категориям и будут посвящены следующие статьи этого цикла.
ПРОДОЛЖЕНИЕ (МОЖЕТ, НУДНОЕ, НО НУЖНОЕ)
Часть 2. Определения множества и подмножества.
Часть 3. Бинарные операции над множествами.
Часть 4. Унарные операции над множествами
Часть 5. Законы де Моргана и диаграммы Эйлера-Венна (выйдет вечером 24.05) — подпишитесь на телеграмм-канал, чтобы не пропустить.
************************************************************************
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.
**************************************************************************
О чем я еще пишу:
Теорема неслучайности: неравенство Чебышева
Про факториал
Ответ тем, кто отрицает пользу математики в обычной жизни
Правда интересные числа, «мамой клянусь»
Экзотические тригонометрические формулы, которые не дают в школе
