Какие свойства электропривода характеризует маховый момент
Иногда возникает необходимость приведения маховых масс электропривода к одной оси. Это приводит к удобству расчета системы электропривода, так как все моменты инерции системы приводятся как правило к валу машины.
Для начала разберемся что такое момент инерции относительно оси – это сумма произведений масс отдельных частей тела, умноженного на квадрат расстояния этой же части тела до оси вращения, которая берется для всего тела:
На практике, как правило, момент инерции довольно часто выражают как произведение квадрата радиуса инерции на массу тела:
m – общая масса всего тела, выраженная в кГсек2/м;
p – радиус инерции тела, выражен он в м;
Радиус инерции – расстояние от оси вращения, которая проходит через центр тяжести объекта, на котором нужно поместить массу объекта, которая будет сосредоточена в одной точке, чтоб она удовлетворяла равенству:
Значения радиусов инерции простейших геометрических тел приведены ниже. Используя формулы приведенные ниже и при условии известности массы тела, можно вычислить момент инерции тела по формулам, приведенным выше:
Если геометрические тела не сложные, то момент инерции можно приблизительно определить как сумму таких моментов отдельных тел , взятых относительно оси вращения. Как пример – момент инерции (далее J) маховика будет равен сумме J спиц, обода и втулки. В случаях, когда точное вычисление J представляется затруднительным, могут оперировать приближенными величинами. Иногда для маховика определяют J обода и прибавляют от 8% до 15% для учета маховых масс спиц. В случае червяка J ротора зубцов принимается 40% J пологого цилиндра соответствующих размеров. Червячное или зубчатое колесо учитывается как полый цилиндр. К полученной величине добавляют 25% для спиц и втулки. Если для зубчатого колеса известны только вес и шаг зацепления, то J могут определять как произведение 60% всего веса на квадрат радиуса длительной окружности.
Приведенный момент инерции (Jпр) входит в уравнение движения электропривода. Jпр – это J простейшей системы, которая состоит из элементов, которые вращаются со скоростью вала или оси, к которой производят приведение, и при этом запас кинетической энергии приведенной системы равен запасу кинетической энергии реальной системы.
Ниже показана реальная система и приведенная
Реальная:
Приведенная:
В таком случае выполнится равенство:
Где: Jпр – приведенный момент инерции в валу электромашины;
J1, J2… Jn, ω1, ω2, ωn – моменты инерции и угловые скорости вращения механизмов или передач машины в соответствующих осях;
Jд, ωд – угловая скорость и момент инерции электродвигателя.
Отсюда очевидно, что:
Где: j1, j2, …, jn – передаточные числа между осями вращающихся звеньев и осью электромашины.
Отсюда следует, что Jпр вращающихся частей равен сумме J каждого отдельного элемента системы относительно своего вала, деленного на квадрат передаточного числа (j), между валом конкретного элемента и валом, к котором приводится момент инерции. Часто при определении Jпр системы его считают равным сумме моментов инерций ротора или якоря электрической машины и Jпр рабочего органа, а также J отдельных звеньев системы передаточного механизма учитывают с помощью увеличения J в δ раз, то есть:
Значение δ обычно лежит в пределах 1,1 ÷ 1,3.
В теории электропривода довольно часто встречается понятия махового момента – GD2, вместо моментов инерций. Если заменить в формуле приведенной выше массу m на вес G и ускорение свободного падения g, а радиус величины инерции p через ее диаметр D, получим следующее выражение:
GD2 выражается в кГм2. Очевидно, что для GD2 также существует соотношение, аналогичное выражению для J:
При введении вместо J в уравнение движение электропривода GD2 получим следующее выражение:
- При постоянном GD2:
- При переменном GD2:
Уравнения движения с использованием GD2 и числа оборотов в минуту могут казаться более удобными для применения на практике, так как скорость вращения вала машины обычно измеряют в оборотах в минуту — об/мин, GD2 – довольно часто публикуют в каталогах. Однако при использовании их следует помнить, что коэффициенты 375 и 7200 – числа, имеющие размерность ускорения. Без учета этих обстоятельств правые части этих выражений не будут иметь размерность момента. Поэтому при сложных расчетах рекомендуется использовать уравнение движения в форме 
или 
.
Âûáîð ýëåêòðîïðèâîäà îïðåäåëÿåòñÿ òðåáîâàíèÿìè ðàáî÷åé ìàøèíû. Ýëåêòðîïðèâîä äîëæåí îáåñïå÷èòü âûïîëíåíèå ðàáî÷åé ìàøèíîé çàäàííîé òåõíîëîãèè ïðè âñåõ âîçìîæíûõ ðåæèìàõ: ïóñêà, ïðèåìà è ñáðîñà íàãðóçêè, òîðìîæåíèÿ, èçìåíåíèÿ ñêîðîñòè, ïîñòîÿííîé íàãðóçêè. Õàðàêòåð ïðîòåêàíèÿ ýòèõ ðåæèìîâ â ïåðâóþ î÷åðåäü îïðåäåëÿåòñÿ ìåõàíè÷åñêèìè ñâîéñòâàìè äâèãàòåëÿ è ðàáî÷åé ìàøèíû. Îäíèì èç îñíîâíûõ êðèòåðèåâ îöåíêè ìåõàíè÷åñêèõ ñâîéñòâ êàê äâèãàòåëÿ, òàê è.ðàáî÷åé ìàøèíû ñëóæàò èõ ìåõàíè÷åñêèå õàðàêòåðèñòèêè.
Ìåõàíè÷åñêèå õàðàêòåðèñòèêè ýëåêòðîäâèãàòåëåé
Ìåõàíè÷åñêîé õàðàêòåðèñòèêîé ýëåêòðîäâèãàòåëÿ íàçûâàåòñÿ çàâèñèìîñòü ñêîðîñòè âðàùåíèÿ âàëà îò ðàçâèâàåìîãî äâèãàòåëåì ìîìåíòà ω=φ(Ìä) èëè n =f(Ìä), ãäå ω — óãëîâàÿ ñêîðîñòü âðàùåíèÿ âàëà, ðàä/ñ, n — ñêîðîñòü âðàùåíèÿ âàëà, îá/ìèí.
Ìåõàíè÷åñêàÿ õàðàêòåðèñòèêà äâèãàòåëÿ íàçûâàåòñÿ åñòåñòâåííîé, åñëè çàâèñèìîñòü n = f (Ì) ïîëó÷åíà ïðè íîìèíàëüíûõ ïàðàìåòðàõ ïèòàþùåé ñåòè, íîðìàëüíîé ñõåìå âêëþ÷åíèÿ è áåç äîáàâî÷íûõ ñîïðîòèâëåíèé â öåïè äâèãàòåëÿ.
Ïðè íàëè÷èè äîáàâî÷íûõ ñîïðîòèâëåíèé èëè ïèòàíèè äâèãàòåëÿ îò ñåòè ñ íàïðÿæåíèåì èëè ÷àñòîòîé, îòëè÷íûìè îò íîìèíàëüíûõ, ìåõàíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëÿ áóäóò íàçûâàòüñÿ èñêóññòâåííûìè. Î÷åâèäíî, ÷òî èñêóññòâåííûõ õàðàêòåðèñòèê äâèãàòåëü èìååò áåñ÷èñëåííîå ìíîæåñòâî, à åñòåñòâåííóþ — òîëüêî îäíó.
Áîëüøèíñòâî ýëåêòðîäâèãàòåëåé ïîä íàãðóçêîé ïðè óâåëè÷åíèè ìîìåíòà ñíèæàåò ñêîðîñòü âðàùåíèÿ. Õàðàêòåðèñòèêó â ýòîì ñëó÷àå íàçûâàþò ïàäàþùåé. Ñòåïåíü èçìåíåíèÿ ñêîðîñòè äâèãàòåëÿ ïðè èçìåíåíèè ìîìåíòà îöåíèâàþò òàê íàçûâàåìîé æåñòêîñòüþ ìåõàíè÷åñêîé õàðàêòåðèñòèêè, êîòîðóþ îïðåäåëÿþò îòíîøåíèåì α = ΔÌ/Δω èëè α = ΔÌ/Δn
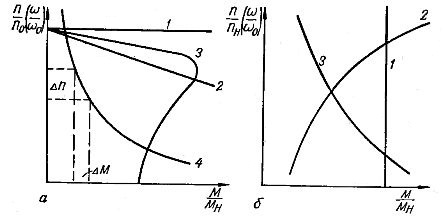
Ðèñ. 1. Ðàçëè÷íûå âèäû ìåõàíè÷åñêèõ õàðàêòåðèñòèê: à — ýëåêòðîäâèãàòåëåé, á — ïðîèçâîäñòâåííûõ ìàøèí.
Âåëè÷èíû èçìåíåíèÿ ìîìåíòà è ïàäåíèÿ ñêîðîñòè ïðè îïðåäåëåíèè æåñòêîñòè áåðóò îáû÷íî â îòíîñèòåëüíûõ åäèíèöàõ. Ýòî äàåò âîçìîæíîñòü ñðàâíèâàòü õàðàêòåðèñòèêè äâèãàòåëåé ðàçëè÷íîãî âèäà.
 çàâèñèìîñòè îò ñòåïåíè æåñòêîñòè âñå ìåõàíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëåé ïîäðàçäåëÿþò íà ñëåäóþùèå ãðóïïû.
1. Àáñîëþòíî æåñòêèå õàðàêòåðèñòèêè ñ âåëè÷èíîé æåñòêîñòè α = ∞. Òàêèå ìåõàíè÷åñêèå õàðàêòåðèñòèêè (êðèâàÿ 1, ðèñ. 1, à) ñî ñòðîãî ïîñòîÿííîé ñêîðîñòüþ âðàùåíèÿ èìåþò ñèíõðîííûå äâèãàòåëè.
2. Æåñòêèå õàðàêòåðèñòèêè ñî ñðàâíèòåëüíî íåáîëüøèì ïàäåíèåì ñêîðîñòè ïðè óâåëè÷åíèè ìîìåíòà è α = 40 — 10. Ê ýòîé ãðóïïå îòíîñÿòñÿ åñòåñòâåííûå õàðàêòåðèñòèêè äâèãàòåëåé ïîñòîÿííîãî òîêà ñ íåçàâèñèìûì âîçáóæäåíèåì (êðèâàÿ 2) è õàðàêòåðèñòèêè àñèíõðîííûõ äâèãàòåëåé â ïðåäåëàõ ëèíåéíîãî ó÷àñòêà (êðèâàÿ 3).
3. Ìÿãêèå ìåõàíè÷åñêèå õàðàêòåðèñòèêè ñ áîëüøèì îòíîñèòåëüíûì ïàäåíèåì ñêîðîñòè ïðè óâåëè÷åíèè ìîìåíòà è ñ æåñòêîñòüþ äî α = 10. Òàêèå õàðàêòåðèñòèêè èìåþò äâèãàòåëè ïîñòîÿííîãî òîêà ñ ïîñëåäîâàòåëüíûì âîçáóæäåíèåì (êðèâàÿ 4), äâèãàòåëè ñ íåçàâèñèìûì âîçáóæäåíèåì ñ áîëüøèì ñîïðîòèâëåíèåì â öåïè ÿêîðÿ è àñèíõðîííûå äâèãàòåëè ñ äîáàâî÷íûìè ñîïðîòèâëåíèÿìè â öåïè ðîòîðà.
Ïðè ðàáîòå ýëåêòðîïðèâîäà äëÿ ïðåîäîëåíèÿ ñîïðîòèâëåíèÿ ðàáî÷åé ìàøèíû äâèãàòåëü äîëæåí ðàçâèâàòü îïðåäåëåííûé ìîìåíò. Ïîýòîìó ïðè âûáîðå äâèãàòåëÿ íåîáõîäèìî âûÿâèòü ïðåæäå âñåãî ñîîòâåòñòâèå õàðàêòåðèñòèê äâèãàòåëÿ è ðàáî÷åé ìàøèíû.
Ìåõàíè÷åñêèå õàðàêòåðèñòèêè ðàáî÷èõ ìàøèí
Ìåõàíè÷åñêîé õàðàêòåðèñòèêîé ðàáî÷åé ìàøèíû íàçûâàþò çàâèñèìîñòü ìîìåíòà ñòàòè÷åñêèõ ñîïðîòèâëåíèé ìàøèíû îò ñêîðîñòè âðàùåíèÿ ïðèâîäíîãî âàëà. Ýòó çàâèñèìîñòü äëÿ óäîáñòâà ñîâìåñòíîãî ïîñòðîåíèÿ âûðàæàþò îáû÷íî òàê æå, êàê è õàðàêòåðèñòèêó äâèãàòåëÿ, â âèäå ω=φ(Ìñ) èëè n =f(Ìñ).
Ìîìåíò ñòàòè÷åñêèõ ñîïðîòèâëåíèé Ìñ, èëè ñîêðàùåííî ñòàòè÷åñêèé ìîìåíò, ïðåäñòàâëÿåò ñîáîé ìîìåíò ñîïðîòèâëåíèÿ, ñîçäàâàåìûé ìàøèíîé íà ïðèâîäíîì âàëó â ñòàòè÷åñêîì (óñòàíîâèâøåìñÿ) ðåæèìå, êîãäà ñêîðîñòü íå èçìåíÿåòñÿ.
Ìåõàíè÷åñêóþ õàðàêòåðèñòèêó ìàøèíû ìîæíî ïîëó÷èòü îïûòíûì ïóòåì èëè ðàñ÷åòîì, åñëè èçâåñòíî ðàñïðåäåëåíèå ñòàòè÷åñêèõ óñèëèé èëè ìîìåíòîâ ïî ýëåìåíòàì êèíåìàòè÷åñêîé ñõåìû. Ñòàòè÷åñêèå ìîìåíòû ìàøèí ìîãóò çàâèñåòü íå òîëüêî îò ñêîðîñòè, íî è îò äðóãèõ âåëè÷èí, ïîýòîìó ïðè ïðàêòè÷åñêèõ ðàñ÷åòàõ ýëåêòðîïðèâîäîâ íåîáõîäèìî ðàññìàòðèâàòü êàæäûé ñëó÷àé â îòäåëüíîñòè.
Ñòàòè÷åñêèå ìîìåíòû ðàçëè÷íûõ ðàáî÷èõ ìàøèí ïî õàðàêòåðó çàâèñèìîñòè èõ îò ñêîðîñòè (ìåõàíè÷åñêèå õàðàêòåðèñòèêè) ïîäðàçäåëÿþò íà ãðóïïû. Íàèáîëåå ÷àñòî âñòðå÷àþùèåñÿ íà ïðàêòèêå èç íèõ ñëåäóþùèå.
1. Ñòàòè÷åñêèé ìîìåíò ìàëî çàâèñèò èëè ïðàêòè÷åñêè íå çàâèñèò îò ñêîðîñòè (êðèâàÿ 1, ðèñ. 2, á). Òàêèå õàðàêòåðèñòèêè èìåþò ïîäúåìíûå ìåõàíèçìû, êðàíû, ëåáåäêè, òåëüôåðû, à òàêæå ëåíòî÷íûå òðàíñïîðòåðû ïðè ïîñòîÿííîé íàãðóçêå.
2. Ñòàòè÷åñêèé ìîìåíò ìàøèíû âîçðàñòàåò ïðîïîðöèîíàëüíî êâàäðàòó ñêîðîñòè (êðèâàÿ 2). Ýòó õàðàêòåðèñòèêó, òèïè÷íóþ äëÿ îñåâûõ âåíòèëÿòîðîâ, íàçûâàþò âåíòèëÿòîðíîé õàðàêòåðèñòèêîé è àíàëèòè÷åñêè ïðåäñòàâëÿþò â âèäå ôîðìóëû: Mc = Mî+kn2, ãäå Ìî — íà÷àëüíûé ñòàòè÷åñêèé ìîìåíò, îáóñëîâëåííûé ÷àùå âñåãî ñèëàìè òðåíèÿ, êîòîðûå îáû÷íî íå çàâèñÿò îò ñêîðîñòè, k — îïûòíûé êîýôôèöèåíò. Êðîìå âåíòèëÿòîðîâ, âåíòèëÿòîðíûìè õàðàêòåðèñòèêàìè îáëàäàþò öåíòðîáåæíûå è âèõðåâûå íàñîñû, ñåïàðàòîðû, öåíòðèôóãè, ãðåáíûå âèíòû, òóðáîêîìïðåññîðû è áàðàáàíû ìîëîòèëîê íà õîëîñòîì õîäó.
3. Ñòàòè÷åñêèé ìîìåíò óìåíüøàåòñÿ ïðè óâåëè÷åíèè ñêîðîñòè (êðèâàÿ 3). Ê ýòîé ãðóïïå îòíîñÿòñÿ õàðàêòåðèñòèêè íåêîòîðûõ òðàíñïîðòåðíûõ ìåõàíèçìîâ è íåêîòîðûõ ìåòàëëîðåæóùèõ ñòàíêîâ.
4. Ñòàòè÷åñêèé ìîìåíò èçìåíÿåòñÿ îò ñêîðîñòè íåîäíîçíà÷íî, ñ ðåçêèì ïåðåõîäîì, îáóñëîâëåííûì îñîáåííîñòüþ òåõíîëîãè÷åñêîãî ïðîöåññà. Õàðàêòåðèñòèêè ýòîé ãðóïïû èìåþò ìàøèíû, ðàáîòàþùèå ñ ÷àñòûìè áîëüøèìè ïåðåãðóçêàìè, êîòîðûå èíîãäà ïðèâîäÿò ê ïîëíîé îñòàíîâêå. Íàïðèìåð, ìåõàíèçì ÷åðïàíèÿ îäíîêîâøîâîãî ýêñêàâàòîðà, ñêðåáêîâûé òðàíñïîðòåð, ðàáîòàþùèé ïîä çàâàëîì òðàíñïîðòèðóåìîé ìàññû, äðîáèëêè è äðóãèå ìàøèíû.
Êðîìå ïåðå÷èñëåííûõ, íà ïðàêòèêå âñòðå÷àþòñÿ è äðóãèå âèäû ìåõàíè÷åñêèõ õàðàêòåðèñòèê ìàøèí, íàïðèìåð ïîðøíåâûõ íàñîñîâ è êîìïðåññîðîâ, ñòàòè÷åñêèå ìîìåíòû êîòîðûõ çàâèñÿò îò ïóòè.
Мгновенный крутящий момент на валу двигателя определяют по формуле
где D — диаметр цилиндра, м;
R — радиус кривошипа, м;
?р? —значение касательной силы принимается для заданного ? по диаграмме ?P? = f(?).
Так как с изменением ? величина ?P? также изменяется, то крутящий момент Мк не остается постоянным и вследствие этого коленчатый вал двигателя вращается неравномерно, угловая скорость вращения вала изменяется от максимального значения ?mах до минимального ?min. Показателем, характеризующим изменение скорости вращения коленчатого вала, является степень неравномерности вращения ? = ?max – ?min / ?cp, где ?ср= ?max + ?min / 2 . Чем меньше ?, тем равномернее вращается коленчатый вал. Для судовых двигателей, работающих непосредственно на винт, ? = 1/20 : 1/40, а для работающих на электрогенератор ? = 1/100 ? 1/300.
Одним из способов увеличения равномерности вращения является увеличение числа цилиндров, однако по целому ряду обстоятельств число цилиндров бывает ограничено. Вторым способом является применение маховиков, которые, аккумулируя избыточную энергию, сглаживают неравномерность вращения.
Применяя уравнения движения тела, вращающегося около неподвижной оси, к движению коленчатого вала, можно записать
где М — момент сил инерции неравномерно вращающихся масс двигателя; J — суммарный момент инерции всех вращающихся масс двигателя, передачи и гребного вала, приведенный к пальцу кривошипа и принимаемый постоянным; ? — угловая скорость вращения вала;
d? / dt — мгновенное значение углового ускорения вала двигателя.
Из уравнения (175) видно, что с увеличением J уменьшается угловое ускорение, т. е. ход двигателя становится более равномерным. С достаточной для практики точностью можно считать J = J0 = Jм, где J0 — приведенный момент инерции массы КШМ; Jм— момент инерции массы маховика.
Приближенно можно принять: для тронковых двигателей
где ?G — масса поступательно-движущихся частей двигателя, кг;
R — радиус кривошипа, м;
Динамический момент инерции
где L— наибольшая работа крутящего момента, затрачиваемая на увеличение кинетической энергии вращающихся масс двигателя, дж;
п — частота вращения, об/сек.
Величина L определяется из суммарной диаграммы касательных усилий. Для этого на диаграмме ?Р? = f (?) нужно построить линию среднего суммарного касательного усилия Р? ср. Площадь между кривой ?Р? = f (?)и линией Р? ср, лежащей над этой линией, называется избыточной. Она характеризует избыток работы движущих сил, вызывающих ускорение вращения вала и поглощаемых маховиком и вращающимися массами двигателя. В области, где площадь между кривой ?Р? = f (?) и линией Р? ср лежит под этой линией, происходит уменьшение угловой скорости вращения. Если за период ?всп кривая ?Р? = f (?) имеет несколько максимумов, то расчетная величина избыточной работы L определяется следующим образом (рис. 224).
Площадь избыточной работы (лежащие над линией Р? ср) представляют в виде векторов, направленных вверх (f2, f4), а площади затраченной работы (лежащие под линией Р? ср) — в виде векторов, направленных вниз (f1,f2,f5). Алгебраически сложив эти векторы, получают как результирующий вектор площадь f, характеризующую избыточную работу, накопленную системой за цикл. Если на диаграмме суммарных касательных сил масштаб по оси абсцисс l соответствует ?° или ?°?/180 радиан, то 1 м будет соответствовать ?°?/180l радиан.
При масштабе ординат 1 м = а н/м2, масштаб 1 м2 площади составит ?0?a / 180l = с.
Наибольшая избыточная работа L = FRfc, где F — площадь поршня, м2; R — радиус кривошипа, м; f — площадь наибольшей площадки на диаграмме ?Р? cp = f (?).
Определив суммарный момент инерции всех вращающихся масс J и приведенный момент инерции массы КШМ J0, подсчитывают необходимый для поддержания требуемой степени неравномерности момент инерции маховика Jм = J—J0. Если величина Jм ? 0, то маховик не нужен.
Момент инерции маховика Jм можно выразить через его маховой момент
где G0 — масса обода маховика, кг;
dм — диаметр маховика по центру тяжести обода, м.
Из формулы (179), задавшись диаметром маховика dм определяют массу его обода
Так как при этом не учитывают влияния диска маховика, то полученное значение массы обода окажется завышенным. Поэтому массу обода окончательно принимают: G‘о = (0,7?0,9)G0. Полная масса маховика
Приняв форму сечения обода и выбрав для него материал, определяют размеры обода из выражения
где а и b — ширина и толщина обода, м;
? — плотность материала маховика, кг/м3.
Задавшись одним из размеров сечения обода, определяют другой его размер. Диаметр маховика для судовых двигателей принимают не более 2 м, причем исходя из соображений прочности нельзя допускать, чтобы окружная скорость на внешней стороне обода превышала 30—40 м/сек для чугунных маховиков и 40— 60 м/сек для стальных.
ЛАБОРАТОРНАЯ РАБОТА №1 «ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ И МАХОВОГО МОМЕНТА ЭЛЕКТРОПРИВОДА МЕТОДОМ СВОБОДНОГО ВЫБЕГА»
Цель работы:
Определить момент инерции и маховый момент электропривода. Приобрести практические навыки в опытном определении момента инерции электропривода.
Теоретическая часть
Момент инерции (маховый момент) электропривода или двигателя может быть определен экспериментально методами крутильных колебаний, маятниковых колебаний, падающего груза и свободного выбега. Выбор метода зависит от условий проведения эксперимента, наличия оборудования, приборов, возможности разборки двигателя и т.д.
Метод крутильных колебаний. Предварительно двигатель разбирают, чтобы освободить ротор от крышек и подшипников. Ротор за конец вала подвешивают на стальной проволоке, второй конец которой жестко закрепляют в опоре. При этом нужно обеспечить строгую вертикаль оси ротора. Проволоку с подвешенным ротором закручивают из положения равновесия на некоторый угол и подсчитывают число полных колебаний, совершаемых ротором, за достаточно большой промежуток времени t.
Метод маятниковых колебаний. Ротор крепится любым способом, например, проволокой к отрезку угловой стали так, чтобы вершина уголка могла быть использована в качестве призмы, относительно которой ротор совершает колебания. Оба конца полученного маятника опирают на горизонтальные металлические опоры таким образом, чтобы ротор мог совершать колебания относительно точек опоры. Момент инерции ротора относительно оси, совпадающей с вершиной уголка (если пренебречь моментом инерции этого уголка) определится как:
где, G — вес ротора, кг; a — расстояние между осью ротора и осью качания, м.
Метод падающего груза. Недостатком описанных выше двух методов определения момента инерции ротора является необходимость разборки двигателя. Метод падающего груза позволяет определить момент инерции без разборки. На конце вала или шкива на валу навивают несколько витков гибкого шнура. Другому концу шнура с прикрепленным к нему грузом дают возможность опускаться. При эксперименте измеряют время t, за которое груз опускается на высоту h. Момент инерции
где m — масса груза, кг; r — радиус вала или шкива, м; t -время опускания груза, с; h — высота опускания груза, м.
Метод свободного выбега. Изложенные выше методы при значительных размерах и весе ротора становятся малопригодными или совершенно непригодными, если нужно определить момент инерции электропривода и общего махового момента системы электропривода. В подобной ситуации пользуются методом свободного выбега или самоторможения.
Сущность этого метода состоит в следующем. Исследуемый агрегат, включающий в себя электродвигатель и механически соединённые с ним элементы, разгоняется до некоторой установившейся частоты вращения щ в режиме холостого хода. После этого электродвигатель отключают от сети, и наступает процесс свободного выбега. Ротор двигателя и соединенный с ним механизм (если он есть) за счет накопленной кинетической энергии продолжают вращаться. Из-за потерь на трение частота вращения падает. Снижение частоты вращения будет тем больше, чем больше тормозящее действие сил трения и чем меньше запас кинетической энергии. Мощность, затрачиваемая на преодоление сил трения, должна быть равна уменьшению во времени кинетической энергии электропривода. Торможение происходит за счёт внутренних сил трения.
На преодоление этих сил затрачивается кинетическая энергия А, запасённая во вращающихся частях агрегата:
(1)
где Jобщ — общий момент инерции агрегата, ? — угловая частота вращения электродвигателя на холостом ходу (х.х.).
С другой стороны, эта энергия может быть определена как произведение мощности, затраченной на приведение во вращение агрегата в режиме х.х. Pвр.0 на время свободного выбега t:
(2)
Приравняв (1) и (2), получим выражение общего момента инерции
(3)
По полученному значению момента инерции определяют маховый момент:
(4)
По опыту холостого хода и паспортным данным двигателя определяют Pвр.0
где RЯ — сопротивление цепи якоря, I0-ток холостого хода, U0-напряжение холостого хода, Uщ?2В-падение напряжения на щётках.
По кривой выбега определяют t0. Для этого проводят касательную к кривой выбега в точке щ0. Пересечение касательной с осью времени t даст t0.
Задание на выполнение лабораторной работы.
- 1. Снять кривые щ=f(t) свободного выбега и отчеты, выдаваемые лабораторным модулем программы для двух пар двигателей (М1-М2 и М3-М4). Сохранить отчеты в виде файлов с расширением *.txt и графики зависимостей в виде растровых изображений (*.bmp) отдельную папку.
- 2. Рассчитать момент инерции и маховый момент для агрегата М1. Рассчитать момент инерции и маховый момент агрегата М3.
- 3. Оценить моменты инерции электромашинных агрегатов используя габаритные размеры маховиков и паспортные данные двигателей. Плотность железа 7800кг/м3. Сравнить результаты. Паспортные данные двигателей даны в разделе справочные данные для выполнения лабораторных работ.
Методика выполнения
- 1. Запустить программу удаленного управления рабочим столом (см. выше).
- 2. Запустить программу El-drive
- 3. Пройти тест по 1-й лабораторной работе «Проверка знаний»>»Лаб.№1 Свободный выбег»
- 4. После успешного прохождения теста, в меню откроются пункты «Проведение лаб. работ», «Настройки», «Просмотр журнала событий».
- 5. Войти в меню «Настройки» и установить маркер напротив пункта «Режим управления», который позволит управлять стендом с ПК и маркер напротив пункта «Регистрировать по событию»
- 6. Войти в пункт меню «Проведение лаб. работ» выбрать пункт «Лаб. №1 Свободный выбег» и затем «Свободный выбег М1-М2», как показано на рис. 28.
Рис. 28 Запуск лабораторной работы №1
7. В открывшемся окне лабораторной работы №1(см. рис. 29) необходимо выполнить следующие действия:
Рис. 29 Окно лабораторной работы №1
8. В окне лабораторной работы задать параметр «Начальная скорость» равным 90 рад/с.
Рис. 30 Изменение масштаба графика
- 9. Нажать кнопку «Пуск». После окончания построения графика, в меню «Отчет» выбрать пункт «Создать новый», затем из того же меню пункт «Просмотр и редактирование», просмотреть отчет и сохранить его в указанном преподавателем месте или в вашей папке.
- 9.1 Кнопками управления масштабом графика добиться, чтобы он занимал всю площадь координатной плоскости, как показано на рис. 30.
- 9.2 Сохранить результаты эксперимента лабораторной работы как указано в пункте «Методика снятия показаний лабораторных экспериментов в программе El-drive»
- 10. Повторить действия пп. 8.1 — 8.4 для агрегата М3-М4.
- 11. После выполнения лабораторной работы нажать кнопку «Стоп», закрыть окно лабораторной работы, в общем окне программы El-drive нажать кнопку «Общий стоп», закрыть окно программы El-drive.
- 12. Закрыть окно программы уделенного доступа Radmin Viewer 3.0 и Windows Media.
Контрольные вопросы.
- 1. На какие свойства электропривода влияет величина момента инерции и махового момента?
- 2. Как можно изменить момент инерции? С какой целью уменьшают или увеличивают момент инерции?
- 3. Методы определения момента инерции. Их сущность.
- 4. Что такое маховый момент и какова его зависимость от момента инерции?
- 5. На чём основан метод свободного выбега для определения момента инерции?
- 6. Что представляет собой кривая выбега и каков порядок снятия данных для её построения? Научно-техническое предприятие «Центр». Описание лабораторных работ «Электропривод». Могилев, 2005.
- 7. Сущность формул для расчета момента инерции.