Какие свойства является общим для всех функций распределения одномерных случайных величин
ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ
2. ОДНОМЕРНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ
2.1. Случайные величины
Одномерной случайной величиной , или просто случайной величиной,
называют любую числовую функцию, определенную на пространстве элементарных
событий .
Примеры.
1. Рассмотрим пространство элементарных событий, которое
получается в результате независимых бросаний двух монет. В этом примере пространство
элементарных событий состоит из четырех элементарных событий, которым
сопоставляется вероятность 1/4. Определим теперь на этом пространстве случайную
величину , равную числу гербов, появившихся при
бросании двух монет. Очевидно, что значения случайной величины есть
0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5,
0,25, соответственно.
2. Пусть у нас имеется некоторое количество кроликов (N),
среди которых доля альбиносов равна 0.05. Предположим, что мы из общего
количества N кроликов наугад выбрали 40. Рассмотрим пространство
элементарных событий для представления результатов данного
эксперимента. В этом примере пространство элементарных событий состоит из равновероятных
элементарных событий. Определим теперь на этом пространстве случайную величину ,
равную числу альбиносов среди 40 выбранных кроликов. Множество возможных
значений случайной величины есть числа от 0 до 40 включительно.
Из формулы Бернулли следует, что вероятность того, что случайная величина примет
значение i, где i=,
1, 2, …, 40, равна
Так как одномерная случайная величина представляет
собой числовую функцию на пространстве элементарных событии, то любая числовая
функция от случайной величины в соответствии с
определением также является случайной величиной.
2.2. Функция распределения
вероятностей случайной величины
Определение.
Функцией распределения вероятностей, или просто функцией
распределения (иногда применяют термин кумулятивная функция
распределения) случайной величины , называется функция F(х), равная
для любого значения x
вероятности события :
Иногда в литературе применяется другое обозначение
функции распределения вероятностей случайной величины .
Из определения (2.1) легко вывести свойства функции
распределения:
1.
2. F(х) — неубывающая функция
3.
4.
5.
На рис. 2.1 приведен график функции распределения вероятностей
случайной величины из первого примера предшествующего пункта.
Рис. 2.1. Функция
распределения F(x) случайной величины из первого примера 2.1.
2.3. Дискретные случайные величины
Различаются два типа случайных величин: дискретные,
принимающие конечное или счетное число значений, и непрерывные, принимающие все
значения на некотором непрерывном промежутке числовой оси.
Определение.
Дискретной случайной величиной называется
случайная величина, принимающая конечное или счетное множество значений х,
х1, x2,… .
Обозначим множество всех возможных значений, которые
принимает дискретная случайная величина , через x, х1, х2,…,
а вероятности, с которыми принимает
эти значения, — через р, р1, р2,…
. Тогда . Распределение дискретной случайной величины будет
полностью описано, если указать для любого i вероятность
рiтого,
что принимает
значение xi, т.е. . Функция распределения F(x)
дискретной случайной величины при этом оказывается равной
.
Таким образом, F(x) —
ступенчатая функция, равная постоянной на любом интервале, не содержащем точек xi, и
имеющая в каждой точке xiскачок
вверх на величину pi.
Таким образом, чтобы задать дискретную случайную
величину , достаточно описать множество всех
возможных значений случайной величины x, х1, х2,…, а также указать числа рi такие, что
1.
2.
Наиболее распространенными формами представления
дискретных случайных величин являются табличная
и графическая (рис. 2.2-2.5), отображающие зависимость
—вероятности рi от
возможного значения случайной величины xi. Функция , выражающая эту зависимость, называется
распределением вероятностей дискретной случайной величины.
Наиболее известными примерами дискретных случайных
величин являются: случайная величина, распределенная по дискретному
равномерному закону, биномиально распределенная
случайная величина, случайная величина, распределенная по закону Бернулли,
случайная величина, распределенная по закону Пуассона.
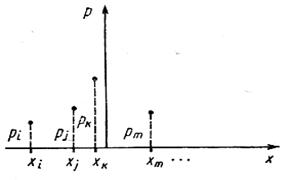
Рис.2.2. Распределение вероятностей дискретной
случайной величины.
Случайная величина, принимающая п() значений х1, х2,…,
xn с вероятностями рi=1/п, называется случайной величиной,
распределенной по дискретному равномерному закону. На рис. 2.3
рассматриваемая случайная величина (для n=6) представлена в графической форме. Случайная
величина, распределенная по дискретному равномерному закону, является моделью
событий с равновероятными исходами (см. пример с бросанием игральной кости).
Рис.2.3. Распределение
вероятностей дискретного равномерного распределения (n=6).
Случайная величина, принимающая два значения: 0 и 1 с
вероятностями q=1-р и р,
соответственно(0<р<1),
называется случайной величиной, распределенной по закону Бернулли
спараметром p.
Случайная величина, распределенная по закону Бернулли — это удачная модель для
описания многих конкретных испытаний, имеющих два исхода (наиболее известный
пример — бросание правильной монеты; здесь p=q=1/2), в том числе и в биологии: присутствие
или отсутствие некоторого признака: пол родившегося цыпленка, цвет цветка и т.
д..
Случайная величина , принимающая п+1
значение 0, 1, 2,…, п, с
вероятностями
где i=0, 1,
2,…, n, q=1-р, 0<p<1, называется биноминально
распределенной случайной величиной, а п
и р — параметрами распределения.
На рис. 2.4 биномиальная случайная величина
представлена в графической форме. Пример использования биномиальной случайной
величины дан в 2.1.
Рис. 2.4. Распределение вероятностей биномиально
распределенной случайной величины для n=10 и p=0.2.
Заметим также, что случайная величина, распределенная
по закону Бернулли, является частным случаем биномиальной случайной величины
для n=1.
Случайная величина , принимающая счетное
множество значений 0, 1, 2,…, с вероятностями
где i=,
1, 2, …, называется случайной величиной,
распределенной по закону Пуассона. Величина называется
параметром распределения Пуассона.
На рис. 2.5 случайная величина, распределенная по
закону Пуассона, представлена в графической форме. Случайная величина,
распределенная по закону Пуассона, служит моделью эксперимента, связанного с
определением численности бактерий в единице объема, или численности животных на
единицу площади, и других подобных экспериментов.
Рис. 2.5. Распределение
вероятностей Пуассоновской случайной величины с λ=5.
Распределение Пуассона иногда называют
«распределением вероятностей редких событий» поскольку оно хорошо
описывает ситуацию случайно и независимо друг от друга появляющихся
событий в течение заданного периода времени (регистрации радиоактивных
частиц в счетчике Гейгера, телефонные звонки, появление посетителей в
малопосещаемом магазине и т.п.). Существенна именно независимость
событий, а их «редкость» требуется лишь для того, чтобы можно было
пренебречь вероятностью одновременного появления двух событий. Если параметр относится
к единице времени, то периоду времени длительностью tбудет
соответствовать пуассоновское распределение с параметром .
Соответственно, вероятность того, что в течение периода t не произойдет ни одного события равна
Если,
например, появление события влечет гибель организма, то можно интерпретировать как вероятность
того, что организм доживет до возраста t. Параметр в этом
случае называют интенсивностью смертности, или просто смертностью. Из
приведенной формулы видно, что чем больше , тем меньше вероятность
дожить до заданного возраста t и, конечно, чем
больше этот заданный возраст, тем меньше вероятность до него дожить (типичный
пример — время жизни стакана в столовой).
1.
Нарисовать
график функции распределения случайной величины, распределенной по закону
Бернулли.
2.
Нарисовать
график функции распределения случайной величины, распределенной по дискретному
равномерному закону (n=6).
3.
Каково
должно быть среднее число бактерий в единичной пробе, чтобы вероятность того,
что в пробе имеется хотя бы одна бактерия, была не меньше 1/2.
4.
Имеется
пять проб воздуха единичного объема, которые в среднем содержат по 2 бактерии в
пробе. Найти вероятность того, что по крайней мере в одной пробе имеется не
менее двух бактерий.
где Q>0.
где .
Предположим, что каждая из п независимых случайных величин (определение независимости случайных величин
будет дано в (4.1) распределена нормально с параметрами 0 и 1 (). Тогда
случайная величина
имеет F—распределение с п и т степенями
свободы (записывается ).
Определение. Непрерывная случайная величина называется
распределенной по логнормальному закону с параметрами и , если случайная величина распределена нормально
().
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 января 2020;
проверки требуют 2 правки.
Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее или равное х, где х — произвольное действительное число. При соблюдении известных условий (см. ниже) полностью определяет случайную величину.
Определение[править | править код]
Пусть дано вероятностное пространство , и на нём определена случайная величина с распределением . Тогда функцией распределения случайной величины называется функция , задаваемая формулой:
.
То есть функцией распределения (вероятностей) случайной величины называют функцию , значение которой в точке равно вероятности события , то есть события, состоящего только из тех элементарных исходов, для которых .
Свойства[править | править код]
- Распределение случайной величины однозначно определяет функцию распределения.
Тождества[править | править код]
Из свойств вероятности следует, что , таких что :
Дискретные распределения[править | править код]
Если случайная величина дискретна, то есть её распределение однозначно задаётся функцией вероятности
,
то функция распределения этой случайной величины кусочно-постоянна и может быть записана как:
.
Эта функция непрерывна во всех точках , таких что , и имеет разрыв первого рода в точках .
Непрерывные распределения[править | править код]
Распределение называется непрерывным, если такова его функция распределения . В этом случае:
,
и
,
а следовательно формулы имеют вид:
,
где означает любой интервал, открытый или закрытый, конечный или бесконечный.
Абсолютно непрерывные распределения[править | править код]
Распределение называется абсолютно непрерывным, если существует неотрицательная почти всюду (относительно меры Лебега) функция , такая что:
.
Функция называется плотностью распределения. Известно, что функция абсолютно непрерывного распределения непрерывна, и, более того, если , то , и
.
Вариации и обобщения[править | править код]
Иногда в российской литературе берётся такое определение функции распределения:
.
Определённая так функция распределения будет непрерывна слева, а не справа.
Многомерные функции распределения[править | править код]
Пусть фиксированное вероятностное пространство, и — случайный вектор. Тогда распределение , называемое распределением случайного вектора или совместным распределением случайных величин , является вероятностной мерой на . Функция этого распределения задаётся по определению следующим образом:
,
где в данном случае обозначает декартово произведение множеств.
Свойства многомерных функций распределения аналогичны одномерному случаю. Также сохраняется взаимно-однозначное соответствие между распределениями на и многомерными функциями распределения. Однако, формулы для вычисления вероятностей существенно усложняются, и потому функции распределения редко используются для .
См. также[править | править код]
- Плотность вероятности
Примечания[править | править код]
Под случайной величиной понимают величину, принимающую свои возможные значения в зависимости от исхода эксперимента, с которым она связана.
Законом распределения (вероятностей) случайной величины называют любое правило, позволяющее найти вероятность того, что случайная величина примет значение из некоторого подмножества своих возможных значений. Общим законом распределения, присущим всем случайным величинам, является функция распределения.
Функцией распределения (вероятностей) случайной величины называется функция действительной переменной , , определяемая формулой .
Каждая функция распределения обладает следующими свойствами:
1) , ; 2) не убывает;
3) , ; 4) непрерывна слева.
Любая неубывающая непрерывная слева действительная функция , удовлетворяющая условиям и , является функцией распределения некоторой случайной величины.
Вероятность события определяется формулой:
.
Случайная величина называется дискретной случайной величиной (ДСВ), если множество её возможных значений конечно или счётно, причём , , где суммирование распространяется на все возможные значения . Функция распределения в этом случае имеет ступенчатый вид и задаётся формулой , где суммирование распространяется на все значения индекса , для которых .
Закон распределения ДСВ удобно задавать рядом распределения. Рядом распределения ДСВ называют таблицу, в которой перечислены все возможные значения этой случайной величины и соответствующие им вероятности . Для наглядности закон распределения ДСВ изображают графически, для чего в прямоугольной системе координат строят точки и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Математическим ожиданием дискретной случайной величины называется число , если ряд сходится абсолютно.
Дисперсией случайной величины называется неотрицательное число . Число называется средним квадратичным отклонением.
Дисперсию дискретной случайной величины вычисляют по формулам:
или .
Пусть -постоянная величина. Математическое ожидание и дисперсия случайной величины обладают следующими свойствами:
Свойства математического ожидания: 1) ; 2) ; 3) ; 4) , если и независимы.
Свойства дисперсии: 1) ; 2) ; 3) ; 4) ; 5) , если и независимы.
Случайная величина называется (абсолютно) непрерывной случайной величиной(НСВ), если её функция распределения представляется в виде , , где -неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности (распределения) вероятностей. Множество возможных значений непрерывной случайной величины несчётно и обычно представляет собой некоторый конечный или бесконечный промежуток числовой прямой.
Функция распределения непрерывной случайной величины является непрерывной неубывающей функцией на всей числовой прямой, причём вероятность попадания в любую фиксированную точку равна нулю: , .
Функция является плотностью вероятностей некоторой НСВ , тогда и только тогда, когда: 1) ; 2) .
Плотность вероятностей в точках, где дифференцируема, определяется равенством: . В точках, где не дифференцируема, плотность вероятностей , определяется произвольным образом, чаще всего по непрерывности слева или справа.
Для непрерывной случайной величины с плотностью вероятностей :
.
Математическим ожиданием непрерывной случайной величины называется число , если интеграл сходится абсолютно.
Дисперсию непрерывной случайной величины вычисляют по формулам:
или .
Медианой непрерывной случайной величины называется число , удовлетворяющее условию или .
Начальным моментом -го порядка ( ) распределения случайной величины (если он существует) называется число .
Центральным моментом -го порядка ( ) распределения случайной величины (если он существует) называется число .
Для непрерывной случайной величины начальные и центральные моменты вычисляют по формулам: , .
2.2 Основные законы распределения одномерных случайных величин.
Дискретная случайная величина имеет биномиальное распределение , если: , .Если ~ , то: , .
Дискретная случайная величина имеет распределение Пуассона если: , .Если ~, то:
, .
Непрерывная случайная величина имеет равномерное распределение ,если: .Если ~, то: , , .
Непрерывная случайная величина имеет показательное распределение ,если: .Если ~, то: , , .
Непрерывная случайная величина имеет нормальное распределение ,если: , . Если ~, то: , , , , где — функция Лапласа, значения которой находят с помощью специальных таблиц.
2.3 Многомерные случайные величины.
Под -мерной случайной величиной (случайным вектором) понимаютсовокупность случайных величин , принимающих свои возможные значения в зависимости от исхода эксперимента, с которым они связаны. Ограничимся рассмотрением двумерных случайных величин , .
Функцией распределения случайного вектора называется функция действительных переменных и , , определяемая формулой .
Зная функцию распределения (совместную) вектора , можно найти функцию распределения (частную) каждой компоненты:
, .
Случайные величины и называются независимыми, если для всех : . В противном случае случайные величины называют зависимыми.
Случайный вектор называется дискретным случайным вектором, если каждая из его компонент является дискретной случайной величиной. Ограничимся рассмотрением дискретных случайных величин и с конечным множеством возможных значений и .
Функция распределения дискретного случайного вектора задаётся формулой , где , , и суммирование распространяется на все значения индексов и для которых и .
Закон распределения дискретного случайного вектора удобно задавать таблицей распределения (вероятностей), в которой перечислены все возможные пары значений ), , компонент вектора и соответствующие им вероятности , причём .
Частные законы распределения , и , компонент и , где , , можно найти, производя в таблице суммирования в каждой строке по столбцам и в каждом столбце по строкам.
Дискретные случайные величины и независимы тогда и только тогда, когда , , , . В противном случае они зависимы.
Ковариацией (корреляционным моментом) случайных величин и называют число . Очевидно, что . Более удобной для вычисления является формула . Для независимых случайных величин и : (необходимое условие независимости).
Коэффициентом корреляциислучайных величин и называют число
, где , .
Коэффициент корреляции обладает свойствами: 1) ; 2) тогда и только тогда, когда и связаны линейной зависимостью , ; 3) если и независимы, то (необходимое условие независимости). Если , то случайные величины и называют некоррелированными.
Условные законы распределения компоненты при , (индекс сохраняет одно и тоже значение при всех возможных значениях ) задают рядами распределения, указывая все возможные значения и соответствующие им условные вероятности: , . Аналогично задают условные законы распределения компоненты при , : , . Условные вероятности компонент и вычисляют соответственно по формулам:
, .
Числовые характеристики , , , , , вычисляют по формулам: , , ,
, .
Условные математические ожидания дискретных случайных величин и при условиях и определяются соответственно формулами: , .
Вероятность события , где — постоянная величина, вычисляется по формуле , где суммирование распространяется на все значения индексов и для которых .
2.4 Функции случайных величин.
Случайную величину , которая каждому исходу ставит в соответствие число , называют функцией от скалярной случайной величины и пишут .
Функция от дискретной случайной величины также является дискретной. Если задана рядом распределения , , то рядом распределения случайной величины является ряд: , , , где — различные числа среди чисел , ( суммирование распространяется на все значения индекса для которых ).
Функция от непрерывной случайной величины может быть как непрерывной, так и дискретной случайной величиной.
Для вычисления числовых характеристик неслучайной функции от случайной величины можно не знать закон распределения зависящей от случайной величины , а достаточно знать закон распределения случайного аргумента . Математическое ожидание и дисперсия случайной величины , где дискретная случайная величина задана рядом распределения , , , могут быть найдены по формулам:
, .
Тема 3. Предельные теоремы теории вероятностей.
Если для неотрицательной случайной величины существует математическое ожидание , то для всех выполняется неравенство:
(первое неравенство Чебышева).
Если для случайной величины существует дисперсия , то для всех выполняется второе неравенство Чебышева:
или
Второе неравенство Чебышева часто используют в виде:
, .
Последовательность случайных величин называют сходящейся по вероятности к случайной величине (кратко записывается ), если для всех : .
Говорят, что для последовательности случайных величин , имеющих математические ожидания , , выполняется закон больших чисел, если , т.е. для всех .
Закон больших чисел в форме Чебышева. Если последовательность независимых случайных величин такова, что существуют и , причём дисперсии этих величин равномерно ограничены (не превышают постоянного числа ), то для неё выполняется закон больших чисел, т.е. . В частности, если случайные величины , являются также одинаково распределёнными (в этом случае , ), то .
Закон больших чисел в форме Бернулли. Если — число успехов в испытаниях по схеме Бернулли с вероятностью успеха в отдельном испытании, то , т.е. для всех .
Закон больших чисел в форме Бернулли является частным случаем закона больших чисел в форме Чебышева.
Центральная предельная теорема. Пусть — последовательность независимых одинаково распределённых случайных величин ( , , ), тогда последовательность нормированных случайных величин , где , сходится по распределению при к стандартной нормальной величине ~ , т.е. для всех : .
Тема 4. Основные понятия и задачи математической статистики. Предварительная обработка экспериментальных данных.
Выборкой объёма из генеральной совокупности называется совокупность наблюдаемых значений случайной величины , соответствующих независимым повторениям случайного эксперимента с которым связана величина . В математической статистике генеральную совокупностьотождествляют со случайной величиной, совокупность всех возможных значений которой и называют генеральной совокупностью.
Выборка может быть записана в виде вариационного и статистического (дискретного или интервального) рядов. Выборку, записанную в виде статистического ряда, называют группированной.
Вариационным рядом выборки называется такой способ её записи, при котором элементы выборки упорядочиваются по величине, т.е. записываются в виде последовательности , где . Разность называется размахом выборки. Всюду в дальнейшем выборочные характеристики будем, как правило, обозначать символом с « » наверху.
Различные значения , ( ), называются вариантами. Число повторений варианты в выборке называется её частотой, а отношение называется её относительной частотой.
Дискретным статистическим рядомназывается упорядоченная в порядке возрастания значений вариант последовательность пар , . Обычно его записывают в виде таблицы, первая стока которой содержит варианты , а вторая их частоты.
Полигоном частотназывается фигура, расположенная под ломаной линией с вершинами в точках , построенных в прямоугольной системе координат.
Интервальным статистическим рядомназывается последовательность пар , , где — непересекающиеся интервалы, как правило, равной длины, объединением которых является отрезок , содержащий все выборочные значения; — частота интервала , равная числу элементов выборки, значения которых попали в данный интервал. Обычно его записывают в виде таблицы, первая строка которой содержит границы интервалов или их середины , а вторая – частоты интервалов.
Гистограммой частотназывается ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группировки так, что площадь каждого прямоугольника равна частоте , . Если длины всех интервалов одинаковы и равны , то высоты прямоугольников равны .
