Какие свойства есть у кривой
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Элементарная геометрия[править | править код]
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».
По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.).
Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.
Определение в топологии[править | править код]
Отображение отрезка[править | править код]
Чаще всего кривая определяется как непрерывное отображение из отрезка в топологическое пространство:
При этом кривые могут быть различными, даже если их образы совпадают.
Такие кривые называют параметризованными кривыми или, если , путями.
Отношение эквивалентности[править | править код]
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
и
эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) из отрезка на отрезок , такая что
Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Комментарий[править | править код]
Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.
Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Кривая Жордана[править | править код]
Кривая Жордана на плоскости с положительной мерой Лебега.
Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство.
В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.
Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.
Кривая Жордана является довольно сложным объектом. Например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, что было сделано Осгудом[1] по аналогии с кривой Пеано.
.
Определение в анализе[править | править код]
В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в ). Пусть и — функции на отрезке , непрерывно дифференцируемые на этом отрезке, и такие, что ни для какого t не равно нулю. Тогда отображение задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле
Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.
Определение в дифференциальной геометрии[править | править код]
Если — гладкое многообразие, можно определить гладкую кривую на как гладкое отображение , дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия равен , то -кривая вводится как кривая, для которой — раз непрерывно дифференцируемое отображение. Если — аналитическое многообразие (например, евклидово пространство) и — аналитическое отображение, кривую называют аналитической.
Гладкие кривые и называются эквивалентными, если существует диффеоморфизм (замена параметра), такой что . Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.
Алгебраические кривые[править | править код]
Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она называется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x2 + y2 + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.
Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.
Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен
после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xn + yn = zn в аффинной форме принимает вид xn + yn = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.
Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:
- Кривые четвёртого порядка: лемниската Бернулли и овал Кассини.
- Кривые шестого порядка: астроида и нефроида.
- Кривая, определяемая уравнением произвольной чётной степени: (многофокусная) лемниската.
Трансцендентные кривые[править | править код]
Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:
Типы кривых[править | править код]
- Замкнутая кривая — кривая у которой начало совпадает с концом.
- Плоская кривая — кривая, все точки которой лежат в одной плоскости.
- Простая кривая — то же, что кривая Жордана.
- Путь — непрерывное отображение отрезка в топологическое пространство.
Типы точек на кривой[править | править код]
- Точка излома
- Касп
- Точка перегиба плоской кривой
- Двойная точка
Обобщённые кривые[править | править код]
Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:
Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.
Важный пример канторовой кривой доставляет ковёр Серпинского.
Какова бы ни была канторова кривая , она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество , гомеоморфное .
Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.
Впоследствии это определение было обобщено Урысоном:
Кривой Урысона называется связное компактное топологическое пространство топологической размерности 1.
Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона.
Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.
См. также[править | править код]
- Кривая Осгуда
- Длина кривой
- Кривая второго порядка
- Кривизна
- Кривые и их каустики
Примечания[править | править код]
- ↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.
Литература[править | править код]
- Болтянский В.Г., Ефремович В.А. Наглядная топология. — М.: Наука, 1982. — 160 с.
- Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии. — Москва, Ижевск: Институт компьютерных исследований, 2004. — 496 с. — (Современная математика). — ISBN 5-93972-300-4.
- Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г.
- Кривые // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Caustics (англ.)
- Surfaces, curves (англ.)
- специальные плоские кривые [1] (рус.)
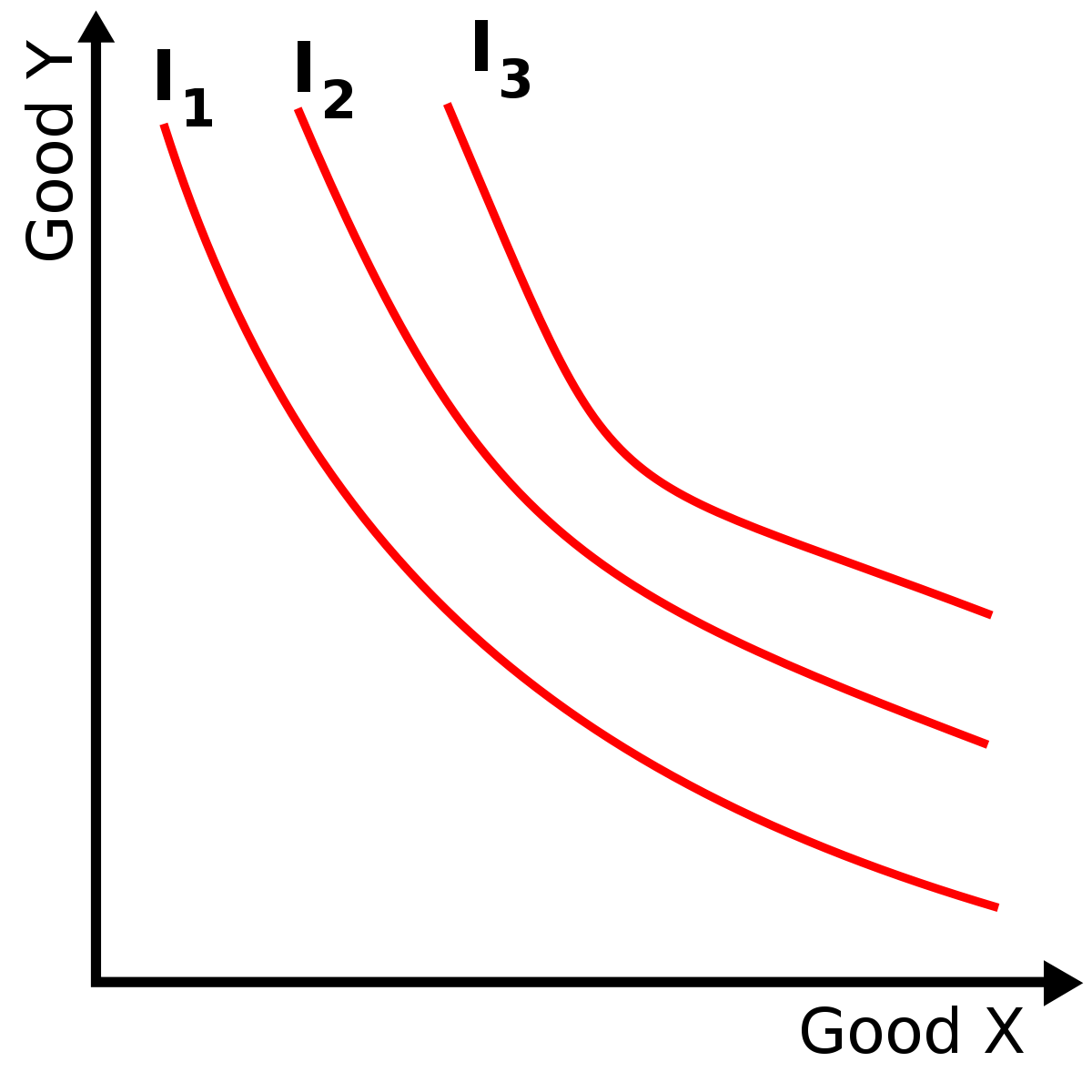
График карты кривых безразличия.
Кривая безразличия — множество всевозможных комбинаций благ, имеющих для потребителя одинаковую полезность и по отношению к выбору которых он безразличен. В простейшем двумерном случае кривую безразличия часто изображают на плоскости в виде выпуклой (к началу координат) линии. Однако кривая имеет такой вид лишь при выполнении ряда условий (см. свойства). Понятие кривой безразличия восходит к Фрэнсису Эджуорту и Вильфредо Парето.
Аналогом понятия кривой безразличия для производителя является изокванта — множество всевозможных комбинаций факторов производства. В простейшем случае в качестве факторов используют труд и капитал.
Кривые безразличия явно или неявно возникают при решении задачи потребителя.
Проблема оценки потребителем полезности благ[править | править код]
Поведение потребителя зависит от двух составляющих: рационализм и иррационализм. Под рационализмом понимается логическая обоснованность каких-либо действий. Иррационализм включает в себя совершение действий под воздействием каких-либо чувств, эмоций, инстинктов, рефлексов и так далее. Целью изучения поведения потребителя является определение предсказуемости его поступков. Однако иррациональная часть поведения в настоящее время является малоизученной и малопредсказуемой. Поэтому можно утверждать, что абсолютно точно предсказать поведение потребителя невозможно. В связи с тем, что иррациональность сложно систематизировать и оценить, в классической экономике предпочитают рассматривать только рациональное поведение потребителя. Оно состоит в сопоставлении результатов потребления и затрат. В качестве результатов рассматриваются изменения полезности, в качестве затрат — суммы денег, потраченные на покупки. Так как в экономике для анализа используются цифры, то первоначально была предпринята попытка оценки полезности. Учёные (Уильям Джевонс, Карл Менгер, Леон Вальрас), которые придерживались данного подхода, назывались кардиналистами. Они понимали, что существует субъективность в оценках различных людей, поэтому пользовались методом индукции, рассматривая оценку среднего потребителя. Благодаря кардиналистам была исследована динамика общей предельной полезности. Другая группа учёных — ординалисты, считали подход кардиналистов неправильным из-за таких обстоятельств как: 1) неспособность точной цифровой оценки, из-за несовершенства информации; 2) переменчивость взглядов потребителя во времени. Взамен точной оценке, ординалисты предложили относительную оценку, которая не нуждалась в цифровой оценке полезности.
Эффект дохода и эффект замещения[править | править код]
Эффект дохода — это результат воздействия на спрос потребителя изменения его реального дохода, вызванного изменением цены товара, без учёта эффекта замещения. Эффект замещения — изменение структуры потребления в результате изменения соотношения цен товаров при неизменном реальном доходе.
Разделение эффекта цены на эффект дохода и замещения позволяет проводить оценку товаров по отношению к доходу. Эффект замещения всегда имеет одно направление: в случае снижения цены он положительный, в случае увеличения — отрицательный. В то же время эффект дохода имеет разное направление: в случае снижения цены эффект дохода положителен, общий эффект цены положительный, значит речь идёт о нормальных товарах. Если в случае снижения цены, эффект дохода отрицательный, а общий эффект положительный, то речь идёт о низших товарах. Если в случае снижения цены эффект дохода отрицательный, общий эффект отрицательный (то есть эффект дохода больше эффекта замещения), то это товар Гиффена.
Практическое значение анализа кривых безразличия[править | править код]
Анализ кривых безразличия используется для определения потребностей различных потребителей с целью изменения различных товаров и услуг. Под видом кривых безразличия подразумевается структура расходов населения, а в случае изменения доходов, каково изменение данной структуры. Также анализ кривых безразличия может быть использован в различных частных ситуациях, связанных, например с осуществлением выбора, в качестве представителя различных направлений социальной политики, в случае подбора различных подарков и т. д.
Формальное определение[править | править код]
Кривая безразличия — это линия (поверхность, гиперповерхность) уровня функции полезности .
При различных (допустимых) значениях константы получается семейство кривых, которое обычно именуется картой безразличия. Математически карта безразличия — это фактормножество в пространстве альтернатив.
Свойства кривых безразличия[править | править код]
Свойства кривых безразличия зависят от свойств функции полезности, которая в свою очередь определяется лежащим в её основе предпочтением.
- Кривые безразличия не могут пересекаться, поскольку не пересекаются линии уровня функции полезности.
- Если предпочтения являются монотонными, то каждая следующая кривая безразличия, проходящая дальше от начала координат, отражает бо́льшую величину полезности, чем предыдущая.
- Из-за монотонности предпочтений кривые безразличия имеют отрицательный наклон.
- Если предпочтения удовлетворяют свойству локальной ненасыщаемости, то кривые безразличия являются «тонкими».
- Предельная норма замещения MRS одного блага другим уменьшается при движении вдоль кривой безразличия, а сами кривые безразличия являются вогнутыми по отношению к началу координат. Это свойство связано с выпуклостью отношения предпочтения (квазивогнутостью функции полезности).
Примеры кривых[править | править код]
Примеры кривых для наиболее распространённых функций полезности.
Форма кривых для «обычных товаров», обладающих частичной заменяемостью.
Встречаются экзотические примеры «кривых» безразличия. Например, карта безразличия для лексикографических предпочтений состоит из отдельных точек.
Литература[править | править код]
- Bruce R. Beattie and Jeffrey T. LaFrance, «The Law of Demand versus Diminishing Marginal Utility» (2006). Review of Agricultural Economics. 28 (2), pp. 263—271.
- Volker Böhm and Hans Haller (1987). «Demand Theory», The New Palgrave: A Dictionary of Economics, v. 1, pp. 785-92.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 мая 2019;
проверки требуют 7 правок.
Кривы́е Безье́ — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Кривая Безье является частным случаем многочленов Бернштейна, описанных русским математиком Сергеем Натановичем Бернштейном в 1912 году.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Кривая Безье относится к частному классу алгебраических кривых, а именно: к кривым 3-го и 2-го порядков соответственно.
Определение[править | править код]
Кривая Безье — параметрическая кривая, задаваемая выражением
где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.
,
где — число сочетаний из по , где — степень полинома, — порядковый номер опорной вершины.
Виды кривых Безье[править | править код]
Линейные кривые[править | править код]
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
.
Квадратичные кривые[править | править код]
Квадратичная кривая Безье
Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: P0, P1 и P2.
.
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF-файлах.
Кубические кривые[править | править код]
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
.
Четыре опорные точки P0, P1, P2 и P3, заданные в 2- или 3-мерном пространстве, определяют форму кривой.
Линия берёт начало из точки P0, направляясь к P1 и заканчивается в точке P3, подходя к ней со стороны P2. То есть, кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.
В матричной форме кубическая кривая Безье записывается следующим образом:
,
где называется базисной матрицей Безье:
В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG)[1], Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
Построение кривых Безье[править | править код]
Линейные кривые[править | править код]
Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
Квадратичные кривые[править | править код]
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия, чтобы параметр t изменялся от 0 до 1:
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
Построение квадратичной кривой Безье | Анимация t: [0;1] |
Кривые высших степеней[править | править код]
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение .
Построение кубической кривой Безье | Анимация t: [0;1] |
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
Построение кривой Безье 4-й степени | Анимация t: [0;1] |
Свойства кривой Безье[править | править код]
- непрерывность заполнения сегмента между начальной и конечной точками;
- кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
- при наличии только двух контрольных точек сегмент представляет собой прямую линию;
- прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
- кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
- масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, так как она с математической точки зрения «аффинно инвариантна»;
- изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
- любой частичный отрезок кривой Безье также является кривой Безье;
- степень (порядок) кривой всегда на одну ступень меньше числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола, так как парабола — кривая 2-го порядка;
- окружность не может быть описана параметрическим уравнением кривой Безье;
- невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые), хотя существуют алгоритмы, строящие приближённую параллельную кривую Безье с приемлемой для практики точностью.
Применение в компьютерной графике[править | править код]
Благодаря простоте задания и манипуляции кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того, аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики, например Adobe Illustrator или Inkscape, подобные фрагменты известны под названием «путей» (path), а в 3DS Max и подобных программах 3D-моделирования кривые Безье имеют название «сплайны».
Преобразование квадратичных кривых Безье в кубические[править | править код]
Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .
См. также[править | править код]
- Поверхность Безье
- NURBS
- B-сплайн
- Кривые
Примечания[править | править код]
Литература[править | править код]
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
Ссылки[править | править код]
- Wolfram Math World Bézier Curve (англ.)
- American Mathematical Society From Bézier to Bernstein (англ.)
- Кривые Безье в компьютерных играх [1] (рус.)
- Часы на кривых Безье (рус.)
- A Primer on Bézier Curves
