Какие свойства дробей вы знаете

В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
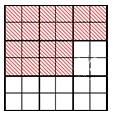
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
У этого термина существуют и другие значения, см. Дробь.
Дробь в математике — число, состоящее из одной или нескольких равных частей (долей) единицы[1]. По способу записи дроби делятся на два формата: обыкновенные вида и десятичные вида .
В математической записи дроби вида или число перед (над) чертой называется числителем, а число после черты (под чертой) — знаменателем. Первый играет роль делимого, второй — делителя.
Обыкновенные дроби с целыми числителями и знаменателями образуют поле рациональных чисел.
Виды дробей[править | править код]
Обыкновенные дроби[править | править код]
Наглядное представление дроби 3/4
Обыкновенная (или простая) дробь — запись рационального числа в виде или где Горизонтальная или косая черта обозначает знак деления, в результате которого получается частное. Делимое называется числителем дроби, а делитель — знаменателем.
Обозначения обыкновенных дробей[править | править код]
Есть несколько видов записи обыкновенных дробей в печатном виде:
Правильные и неправильные дроби[править | править код]
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, у которой модуль числителя больше модуля знаменателя или равен ему, называется неправильной и представляет собой рациональное число, по модулю большее или равное единице.
Например, дроби , и — правильные, в то время как , , и — неправильные. Всякое отличное от нуля целое число можно представить в виде неправильной обыкновенной дроби со знаменателем .
Смешанные дроби[править | править код]
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.
Составные дроби[править | править код]
Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:
или или .
Десятичные дроби[править | править код]
Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом (знак вне аримфетических выражений обычно опускается):
Пример: .
Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.
Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).
Значение дроби и основное свойство дроби[править | править код]
Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.
Если умножить числитель и знаменатель дроби на одинаковую величину:
то значение дроби останется прежним, хотя дроби — разные.
Например:
И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:
— здесь числитель и знаменатель дроби сократили на общий делитель .
Несократимой называется дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме
Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:
— две разные дроби соответствуют одному числу.
Действия с дробями[править | править код]
В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.
Приведение к общему знаменателю[править | править код]
Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: и . Порядок действий:
После этого знаменатели обеих дробей совпадают (равны ). Вместо наименьшего общего кратного можно в простых случаях взять в качестве любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.
Сравнение[править | править код]
Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.
Пример. Сравниваем и . . Приводим дроби к знаменателю .
Следовательно,
Сложение и вычитание[править | править код]
Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:
+ = + =
НОК знаменателей (здесь и ) равно .
Приводим дробь к знаменателю , для этого числитель и знаменатель надо умножить на .
Получилось .
Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на . Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:
— = — =
НОК знаменателей (здесь и ) равно . Приводим дробь к знаменателю , для этого надо числитель и знаменатель умножить на . Получаем .
Умножение и деление[править | править код]
Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:
В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:
В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:
Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую дробь на дробь, обратную второй:
Например:
Преобразование между разными форматами записи[править | править код]
Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:
— бесконечно повторяющийся период принято записывать в круглых скобках.
Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:
История и этимология термина[править | править код]
Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики. Через арабов термин, в переводе на латинский, перешёл в Европу, он упоминается уже у Фибоначчи (1202 год). Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.
Дроби вычислялись ещё в Древнем Египте. До наших дней сохранились математические источники о египетских дробях: Математический папирус Ринда (ок. 1650 год до н. э.)[3], Египетский математический кожаный свиток (XVII век до н. э.)[4], Московский математический папирус (ок. 1850 год до н.э.), Деревянная табличка из Ахмима (англ.) (ок. 1950 год до н.э.)[5].
В Китае обыкновенные дроби встречаются в труде «Математика в девяти книгах» (X-II в до н. э.), отредактированной во II в до н. э. финансовым чиновником Чжан Цаном . Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную[6]. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» (1427 г.) объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на пять веков раньше[7].
Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Современное обозначение обыкновенных дробей происходит из Древней Индии — вначале его позаимствовали арабы, а затем, в XII-XVI веках, — европейцы. Вначале в дробях не использовалась дробная черта: числа записывались таким способом: Использование черты дроби стало постоянным лишь около 300 лет назад. В Европе первым учёным, который использовал и распространял индийскую систему счёта (известную как «арабские цифры»), в том числе способ записи дробей, стал итальянский купец, путешественник, сын городского писаря — Фибоначчи (Леонардо Пизанский)[8]. Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).
В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585). Стевин записывал десятичные дроби сложными способами: например, число 42,53 записывалось как или 42 ⓪ 5 ① 3 ②, где в круге или над строкой означал целую часть, 1 — десятые, 2 — сотые, и так далее. Запятую для отделения целой части стали использовать с XVII века[8].
На Руси дроби называли долями. В первых российских учебниках математики — в XVII веке — дроби назывались ломаными числами[8]. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.
Обобщения[править | править код]
- Кольцо частных
- Рациональная функция — дробь, составленная из многочленов.
См. также[править | править код]
- Дроби в Юникоде
- Цепная дробь
- Египетские дроби
Литература[править | править код]
- Дробь арифметическая // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2. — С. 389—390.
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1982.
- ↑ Дробная черта (Fraction bar, Solidus) — Справочник ПараТайп.
- ↑ The Rhind Mathematical Papyrus (англ.). British Museum. Дата обращения 13 января 2019.
- ↑ Clagett, Marshall. Ancient Egyptian Science: A Source Book. — Philadelphia: American Philosophical Society, 1999. — Т. 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. — С. 17—18, 25, 37—38, 255—257.
- ↑ William K. Simpson. An Additional Fragment from the «Hatnub» Stela // Journal of Near Eastern Studies. — 1961. — Январь (т. 20, № 1). — С. 25—30.
- ↑ Jean-Claude Martzloff. A History of Chinese Mathematics. Springer. 1997. ISBN 3-540-33782-2.
- ↑ Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (англ.). — Princeton University Press, 2007. — P. 518. — ISBN 978-0-691-11485-9.
- ↑ 1 2 3 Математика: Учеб. для 5 кл. средн. шк. / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 4-е изд. — Чебоксары : Чув. кн. изд-во, 1997. — 320 с.: ил. — С. 202—203, 230.
Основное свойство дроби
Если ad=bc, то две дроби frac{a}{b}и frac{c}{d} считаются равными. К примеру, равными будут дроби frac35и frac{9}{15}, так как 3 cdot 15 = 15 cdot 9, frac{12}{7}и frac{24}{14}, так как 12 cdot 14 = 7 cdot 24.
Из определения равенства дробей следует, что равными будут дроби frac{a}{b}и frac{am}{bm}, так как a(bm)=b(am) — наглядный пример применения сочетательного и переместительного свойств умножения натуральных чисел в действии.
Значит frac{a}{b} = frac{am}{bm} — так выглядит основное свойство дроби.
Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.
Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.
Сокращать дроби принято, опираясь на основное свойство дроби.
Например, frac{45}{60}=frac{15}{20}(числитель и знаменатель делится на число 3); полученную дробь снова можно сократить, разделив на 5, то есть frac{15}{20}=frac 34.
Несократимая дробь — это дробь вида frac 34, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.
Приведение дробей к общему знаменателю
Возьмем в качестве примера две дроби: frac{2}{3}и frac{5}{8} с разными знаменателями 3 и 8. Для того, чтобы привести данные дроби к общему знаменателю и сначала перемножим числитель и знаменатель дроби frac{2}{3}на 8. Получаем следующий результат: frac{2 cdot 8}{3 cdot 8} = frac{16}{24}. Затем умножаем числитель и знаменатель дроби frac{5}{8}на 3. Получаем в итоге: frac{5 cdot 3}{8 cdot 3} = frac{15}{24}. Итак, исходные дроби приведены к общему знаменателю 24.
Арифметические действия над обыкновенными дробями
Сложение обыкновенных дробей
а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:
frac{a}{b}+frac{c}{b}=frac{a+c}{b};
б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):
frac{7}{3}+frac{1}{4}=frac{7 cdot 4}{3}+frac{1 cdot 3}{4}=frac{28}{12}+frac{3}{12}=frac{31}{12}.
Вычитание обыкновенных дробей
а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:
frac{a}{b}-frac{c}{b}=frac{a-c}{b};
б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).
Умножение обыкновенных дробей
Умножение дробей подчиняется следующему правилу:
frac{a}{b} cdot frac{c}{d}=frac{a cdot c}{b cdot d},
то есть перемножают отдельно числители и знаменатели.
Например:
frac{3}{5} cdot frac{4}{8} = frac{3 cdot 4}{5 cdot 8}=frac{12}{40}.
Деление обыкновенных дробей
Деление дробей производят следующим способом:
frac{a}{b} : frac{c}{d}= frac{ad}{bc},
то есть дробь frac{a}{b} умножается на дробь frac{d}{c}.
Пример: frac{7}{2} : frac{1}{8}=frac{7}{2} cdot frac{8}{1}=frac{7 cdot 8}{2 cdot 1}=frac{56}{2}.
Взаимно обратные числа
Если ab=1, то число b является обратным числом для числа a.
Пример: для числа 9 обратным является frac{1}{9}, так как 9 cdot frac{1}{9}=1, для числа 5 — frac{1}{5}, так как 5 cdot frac{1}{5}=1.
Десятичные дроби
Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10,000, …, 10^n.
Например: frac{6}{10}=0,6;enspace frac{44}{1000}=0,044.
Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.
Например: 5frac{1}{10}=5,1;enspace frac{763}{100}=7frac{63}{100}=7,63.
В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.
Пример: 5 — делитель числа 100, поэтому дробь frac{1}{5}=frac{1 cdot 20}{5 cdot 20}=frac{20}{100}=0,2.
Арифметические действия над десятичными дробями
Сложение десятичных дробей
Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.

Вычитание десятичных дробей
Выполняется аналогично сложению.

Умножение десятичных дробей
При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Давайте выполним умножение 2,7 на 1,3. Имеем 27 cdot 13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=2). В итоге получаем 2,7 cdot 1,3=3,51.
Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).
Например: 1,47 cdot 10,000 = 14 700.
Деление десятичных дробей
Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:
.png)
Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:
.png)
Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.
2,8 : 0,09= frac{28}{10} : frac {9}{100}= frac{28 cdot 100}{10 cdot 9}=frac{280}{9}=31 frac{1}{9}.
