Какие свойства доказывают поперечность электромагнитных волн
Векторы напряженности электрического ($overrightarrow{E}$) и магнитного ($overrightarrow{H}$) полей в электромагнитной волне всегда взаимно перпендикулярны, они находятся в плоскости перпендикулярной вектору скорости волны ($overrightarrow{v}$). Из вышесказанного следует, что электромагнитные волны являются поперечными. Ориентация векторов (взаимная) $overrightarrow{E}$, $overrightarrow{H}, overrightarrow{v}$ подчиняется правилу: Если смотреть из конца вектора скорости, то вращение от вектора напряжённости электрического поля по кратчайшему направлению к вектору напряженности магнитного поля идет против часовой стрелки (рис.1). Или, вектор $overrightarrow{v}$ имеет направление, как и векторное произведение $overrightarrow{E}$ на $overrightarrow{H}$:
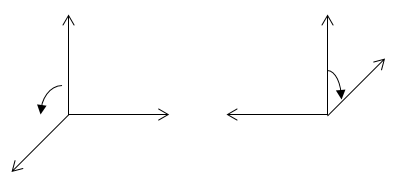
Рисунок 1.
Электромагнитное поле в однородной, изотропной, непроводящей среде, не имеющей сегнетоэлектрических и ферромагнитных веществ, можно описать с помощью векторных уравнений Максвелла в дифференциальной форме:
Или в скалярном виде:
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Рассмотрим плоскую электромагнитную волну, покажем, что она является поперечной, и $overrightarrow{E}bot overrightarrow{H}$. Допустим, что волна распространяется вдоль положительного направления $оси X$. В таком случае имеем:
Из первых уравнений систем (6) и (7) и уравнений (8) и (9) следует, что:
Из системы уравнений (12) можно сделать вывод о том, что $E_x и H_x$ не зависят ни от координат, ни от времени. Подобное стационарное и однородное поле не имеет отношения к электромагнитным волнам, поле которых нестационарное и неоднородное. Так, для поля плоской волны, которая распространяется вдоль $оси X$, имеем:
Колебания векторов $overrightarrow{E}$ и $overrightarrow{H}$ в точках плоскости $x=const$ отстают по времени от колебаний этих же векторов в точках плоскости $x=0$ на величину, равную $frac{x}{v}$, где $v$ — скорость волны. Значит, $overrightarrow{E}$ и $overrightarrow{H}$ зависят от комбинации времени $(t)$ и отношения $frac{x}{v}$ вида ($t-frac{x}{v}$):
Введем обозначение вида: $xi =t-frac{x}{v},$ тогда получим выражения:
Подставим производные из (16) и (17) во второе и третье равнения систем выражений (6) и (7), получим:
Если учесть, что:
то уравнения (18) можно переписать в виде:
Интегрируя выражения (20) по $xi $, положив постоянные интегрирования равными нулю, так как векторы $overrightarrow{E}$ и $overrightarrow{H}$ и их проекции на оси координат для переменного поля плоской волны не могут иметь постоянных составляющих, которые не зависят от $xi =t-frac{x}{v}$, в результате имеем:
Если скалярное произведение векторов будет равно нулю, при этом ни один из этих векторов не равен нулю, значит, эти векторы перпендикулярны. Найдем $overrightarrow{E}cdot overrightarrow{H}$, используя выражение (21):
Из (22) очевидно, что $overrightarrow{E}bot overrightarrow{H}$.
Взаимно перпендикулярные векторы $overrightarrow{E}иoverrightarrow{H}$ колеблются в одной фазе, они одновременно становятся равными нулю и достигают максимума. Для любой бегущей волны, имеющей любую форму волновой поверхности, выполняется равенство:
Пример 1
Задание: Покажите, что векторы $overrightarrow{v}, overrightarrow{E, }overrightarrow{H}$ образуют правую тройку взаимно перпендикулярных векторов.
Решение:
Рассмотрим плоскую электромагнитную волну. Для нее если $overrightarrow{E}=E_yoverrightarrow{j}$, то $overrightarrow{H}=H_zoverrightarrow{k}$, причем если $E_y>0$, то и
[H_z=sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}}E_y>0.]
Это доказывает, что $overrightarrow{v}, overrightarrow{E, }overrightarrow{H}$ — правая тройка взаимно перпендикулярных векторов.
Пример 2
Задание: Покажите на примере плоской электромагнитной волны, что векторы $overrightarrow{E, }overrightarrow{H} $совершают колебания в одной фазе.
Решение:
Из дифференциальных уравнений Максвелла следует, что для плоской электромагнитной волны, которая распространяется вдоль положительного направления $оси X$, выполняются равенства:
[E_x=H_x=0 (2.1),] [E_y=f_1left(t-frac{x}{v}right),E_z=f_2left(t-frac{x}{v}right)(2.2) ,] [H_y={varphi }_1left(t-frac{x}{v}right),H_z={varphi }_2left(t-frac{x}{v}right)(2.3).] [f_1=sqrt{frac{mu {mu }_0}{varepsilon {varepsilon }_0}}{varphi }_2, f_2=-sqrt{frac{mu {mu }_0}{varepsilon {varepsilon }_0}}{varphi }_1(2.4),]
следовательно, можно записать, что:
[H_y=-sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}} E_z, H_z=-sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}} E_yleft(2.5right).]
Зная, что:
[H=sqrt{{H_y}^2+{H_z}^2}и E=sqrt{{E_y}^2+{E_z}^2}left(2.6right).]
Получим:
[sqrt{mu {mu }_0}H=sqrt{varepsilon {varepsilon }_0}E.]
Что означает, что векторы напряженности электрического и магнитного полей совершают колебания в одной фазе.
Система уравнений Максвелла
Приведем законы, которым подчиняется поведение электрического и магнитного полей, лежащие в основе теории электромагнетизма. Эти законы, являющиеся обобщением опыта, формулируются ниже в интегральной форме, так как именно в таком виде обычно выражаются данные эксперимента. Используя основные положения векторного анализа, можно записать эти законы электромагнитного поля в дифференциальной форме.
Если исследуют электромагнитное поле в каком-либо веществе, изотропно заполняющем пространство, то значение векторов Е и В получаются при усреднении микроскопических величин <Eмикр>=Е и <Hмикр>=В. Такая запись позволяет оперировать с мгновенными напряженностями электрического и магнитного полей в любой точке пространства.
Усреднение микроскопических величин законно в том случае, линейные размеры области, где <Eмикр> и<Hмикр> можно считать неизменными ,значительно превышают размеры атомов (молеукл). Длина волны является тем отрезком , на котором напряженность поля сильно изменяется. Поэтому усреднение можно проводить лишь в том случае, когда значительно больше атомных размеров .Такое равенство соблюдается для всего оптического диапазона спектра, включая короткие ультрафиолетовые лучи. Сложнее обстоит дело в рентгеновской области спектра, где см, т.е. того же порядка что размеры атомов.
При переходе к дифференциальной форме законов электромагнитного поля используют следующие теоремы векторного анализа:
Теорема Гаусса о преобразовании поверхностного интеграла в объемный: . (2.3.1)
Теорема Стокса о преобразовании интеграла по замкнутой кривой в поверхностный интеграл (поток ротора через поверхность, охватываемую исследуемой кривой):
. (2.3.2)
Итак , вспомним законы электрического и магнитного полей. Первый из них — основной закон электростатики — закон Кулона. Как следствие этого закона формулируется теорема Гаусса о потоке, которая при наличии диэлектриков в исследуемом пространстве записывается в виде
. (2.3.3)
Отсюда указанным выше способом переходим к дифференциальной форме закона
, (2.3.3а)
где D — вектор электрического смещения, — объемная плотность зарядов.
Существенно, что выражения (2.3.3) и (2.3.3а), полученные из уравнений электростатики, обобщаются Максвеллом для переменных полей, где D и зависят от времени .
Отсутствие в природе магнитных зарядов (монополей) приводит к выражению
(2.3.4)
которое преобразуется к виду
div B = 0. (2.3.4а)
Эти формулы соответствуют хорошо известным модельным представлением о силовых линиях электрического поля, начинающихся на положительных зарядах и заканчивающихся на отрицательных, тогда как линии магнитного поля замкнуты и охватывают породившие их токи. Введение понятия линий электрического и магнитного полей совершенно не обязательно (смысл законов содержится в приведенных формулах), но, как и во многих случаях, наглядность модельных представлений помогает пониманию явления.
Переходя к описанию свойств электрического тока. сформулируем основной закон о зависимости напряженности магнитного поля от силы породившего его тока. Этот закон обычно связывают с именами Био, Савара и Лаплпса. Запишем его в виде, который называют теоремой о циркуляции вектора Н:
Рис. 2.3.5. Теорема о циркуляции вектора Н
Дифференциальная форма этого закона получается применением теоремы Стокса к равенству (2.3.5) и описывает плотности тока j с напряженностью магнитного поля в данной точке:
Рис. 2.3.6. Теорема Стокса
Как известно, Максвелл ввел ток смещения, плотность которого удовлетворяет соотношению
плотность тока
Ток проводимости и ток смещения дополняют друг друга, образуя полный ток плотностью
плотность полного тока
которая, согласно Максвеллу, и фигурирует в уравнении (2.3.6) последним из требующихся нам фундаментальных соотношений является математическая формулировка знаменитого открытия Фарадея — закона электромагнитной индукции.
Рис. 2.3.7. Закон электромагнитной индукции
в котором электродвижущая сила 
, возникающая в замкнутом контуре, связывается со скоростью изменения потока магнитной индукции Ф, пронизывающего этот контур.
При соблюдении некоторых условий эксперимента ( в частности , если контур с током неподвижен и не деформируется за время изменений ) справедлива следующая интегральная форма записи закона индукции:
Рис. 2.3.8. Интегральная форма записи закона индукции
откуда легко получается дифференциальная форма закона
Рис. 2.3.9. Дифференциальная форма записи закона индукции
Здесь уместно сделать следующее значения:
1. Хорошо известны соображения о вихревом характере электрического поля, порождаемого изменяющимся во времени магнитным полем. Это переменное электрическое поле существенно отличается от потенциального электростатического поля , создаваемого системой неподвижных электрических зарядов, для которого rotE = 0. В последующем нас будет интересовать именно переменное электрическое поле . Но , как было показано Максвеллом , наличие переменного электрического поля с неизбежностью приводит к возникновению связанного с ним магнитного поля и поэтому нужно говорить о едином электромагнитном поле , характеризуемом в каждой точке пространства взаимосвязанными ортогональными векторами Е и В.
2. Введение Максвеллом понятий тока смещения в начале выглядело как гениальная догадка. Но несовместимость сформулированного уравнения электромагнитного поля (2.3.6) и уравнения непрерывности
Рис. 2.3.10. Уравнение непрерывности
выражающего одно из самых общих свойств материи — закон сохранения электрического заряда, — с неизбежностью приводит к необходимости введения дополнительного слагаемого в правую часть уравнения поля. Следовательно, уравнение (2.3.6) должно иметь вид
Уравнение теоремы Стокса
Именно это изменяющееся во времени электрическое поле , столь неудачно названо «током смещения», и связанное с ним магнитное поле будут играть главную роль в дальнейшем изложении.
Итак, имеем уравнение электромагнитного поля в следующем виде:
, 
,
, 
. (2.3.11)
Их нужно дополнить «материальными» уравнениями, учитывающими соотношения между векторами Е,D,В,Н и j. При отсутствии ферромагнитных сегнетоэлектрических материалов для изотропных сред можно записать эти уравнения при помощи трех констант: 
(электропроводность), 
(диэлектрическая проницаемость) и 
(магнитная проницаемость), постулируя линейную связь между D и Е, В и Н, j и E, т.е.
D =E , В = Н, j = E. (2.3.12)
Следует также сформулировать граничные условия для уравнений электромагнитного поля, из которых наиболее широко будем использовать равенство тангенциальных составляющих Е и Н на границе раздела двух сред, т.е.
, 
(2.3.13)
если предположить, что граничащие среды разделены слоем, в котором константы , и изменяются непрерывно, а j и конечны, то при стремлении к нулю толщины этого слоя уравнения (2.3.9) и (2.3.6) сведутся к равенствам (2.3.14). Однако при решении конкретных задач часто возникает необходимость задать значение искомых функций на границе исследуемой области. Такие граничные условия определяются условиями эксперимента и не вытекают из уравнений электромагнитного поля. Они должны быть добавлены к системе уравнений (2.3.11). В частности, при рассмотрении безграничного пространства часто задают вид тех или иных функций на бесконечности, руководствуясь физическими условиями решаемой задачи.
Система уравнений, включающая в себя уравнения электромагнитного поля, «материальные» соотношения и граничные условия, названа системой уравнений Максвелла и играетв электродинамике ту же роль. что и аксиоматика уравнений Ньютона в классической механике.
Поперечность электромагнитных волн
Допустим, что волны распространяются в однородном незаряженном диэлектрике. Применим к ним фундаментальные уравнения Максвелла
И материальные уравнения D =E , В = Н.
Пусть волна — плоская и монохроматическая. Запишем ее в комплексном виде
, 
(2.3.15)
где 
— круговая частота, k- волновой вектор, а амплитуды 
постоянны. Дифференцируя по времени, получаем 
, т.е. операция дифференцирования в этом случае сводится к умножению на 
. Аналогично, дифференцирование по координатам x, y, z сводится к умножению на 
. Заметив это и обозначая координатные орты через 
получаем
и аналогично для rot E. В результате уравнения Максвелла перейдут в
Рис. 2.3.16. Уравнение Максвелла
Введем единичный вектор N нормали к фронту волны и скорость распространения последнего в направлении этой нормали — так называемую нормальную скорость v.
Тогда 
(2.3.17)
И предыдущие соотношения перейдут в
(2.3.18)
отсюда видно, что векторы E, H, v в плоской электромагнитной волне взаимно перпендикулярны . Перпендикулярность векторов Е и Н к вектору v, или, что то же, к направлению распространения волны, означает, что электромагнитные волны поперечны. Т.е. проблема поперечности световых волн, с которой не могли справиться теории механического эфира, совсем не возникает в электромагнитной теории света.
Скорость электромагнитной волны
Из уравнений Максвелла можно определить и скорость электромагнитной волны v. С этой целью запишем эти уравнения в скалярной форме:
или
Отсюда после почленного перемножения и сокращения на ЕН получаем для v и показателя преломления 
следующие выражения:
, 
Последнее соотношение называется законом Максвелла. Для немагнитных сред (
) оно переходит в 
.
В вакууме v=c, т.е. v совпадает с электродинамической постоянной с. Тем самым раскрывается глубокий смысл открытия В.Вебера и Кольрауша, впервые измеривших эту постоянную в 1856г.
Энергия переносимая электромагнитной волной
Электромагнитная волна представляет собой электромагнитное возмущение распространяющееся, как уже говорилось, в вакууме со скорость c, а в среде — со скоростью 
. С этим электромагнитным возмущением связанна энергия, плотность которой (т.е. энергия, заключенная в единице объема) выражается для электрического поля через 
, а для магнитного поля через 
. В случае монохроматической волны 
и 
, так что энергия волны пропорциональна квадрату ее амплитуды. Это соотношение между энергией и амплитудой сохраняет свое значение и для любой другой волны.
При распространении электромагнитной волны происходит перенос энергии, подобно тому как это имеет место при распространении упругой волны. Вопрос о течении энергии в упругой волне был впервые (1874г.) рассмотрен Н. А. Умовым который доказал общую теорему о потоке энергии в любой среде. Поток энергии в упругой волне может быть вычислен через величины, характеризующие потенциальную энергию упругой деформации и кинетическую энергию движения частиц упругой среды. Плотность потока энергии выражается с помощью специального вектора (вектор Умова). Аналогичное рассмотрение плодотворно и для электромагнитных. До известной степени можно уподобить энергию электрического поля потенциальной энергии упругой деформации, а энергию магнитного поля — кинетической энергии движения частей деформированного тела. Так же как и в случае упругой деформации, передача энергии от точки к точке в электромагнитной волне связанна с тем обстоятельством, что волны электрической магнитной напряженности находятся в одной фазе. Такая волна называется бегущей. Движение энергии в бегущей упругой волне удобно изображается с помощью вектора S, который можно назвать вектором энергии и который показывает, какое количество энергии протекает в волне за 1с. через 1 метр в квадрате. Для электромагнитных волн вектор этот был введен Пойтингом (1884г.) Его уместно называть вектором Умова-Пойтинга.
Нетрудно найти выражение этого вектора для простого случая, рассмотренного нами в пункте 2.2 и выражающего распространение полоской электромагнитной волны вдоль оси x.
Умножив 
на Н и 
на Е и сложив,
получим 
где 
есть плотность энергии. Рассматривая поток энергии S, входящий и выходящий из элементарного объема, найдем выражение для изменения плотности энергии по времени
Отсюда
Рис. 2.3.19. Численное выражение вектора Умова – Пойтинга для электромагнитной волны
что представляет собой численное выражение вектора Умова — Пойтинга для электромагнитной волны. Что касается направления вектора Умова — Пойтинга, то он перпендикулярен к плоскости, проходящей через векторы электрической м магнитной напряженности, т.е. в векторной форме запишется в общем виде
Своим направление вектор Умова — Пойтинаг определяет направление переноса энергии волны и может бать во многих случаях принят за направление светового луча. Не следует, однако, забывать, что понятие луча есть понятие геометрической оптики и не имеет вполне соответствующего образа в области волновых представлений, для которых введен вектор Умова — -Пойтинга.
Недостаточно обладать мудростью, нужно уметь пользоваться ею.
Информационный блок Электромагнитные волны и их свойства
Общие свойства электромагнитных волн
-Поглощение диэлектрическими
телами
-Отражение (металлами)
-Преломление на границе
диэлектрика
-Поперечность
-Скорость в вакууме (воздухе)
300000 км/с
-Давление на
вещество
-Скорость в
среде убывает
-Интерференция,
дифракция, поляризация
Поглощение
электромагнитных волн. Располагают рупоры друг против друга и, добившись хорошей слышимости звука
в громкоговорителе, помещают между рупорами различные диэлектрические тела. При
этом замечают уменьшение громкости.
Отражение
электромагнитных волн. Если диэлектрик заменить металлической пластиной, то звук перестанет быть
слышимым. Волны не достигают приемника вследствие отражения. Отражение
происходит под углом, равным углу падения, как и в случае световых и
механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми
углами к большому металлическому листу. Звук исчезнет, если убрать
лист или повернуть его.
Преломление
электромагнитных волн. Электромагнитные волны изменяют свое направление (преломляются) на границе
диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из
парафина. Рупоры располагают под углом друг к другу, как и при демонстрации
отражения. Металлический лист заменяют затем призмой. Убирая призму
или поворачивая ее, наблюдают исчезновение звука.
Поперечность
электромагнитных волн. Электромагнитные волны являются поперечными. Это означает, что векторы Е и В электромагнитного поля волны
перпендикулярны направлению ее распространения. При этом векторы Е и В взаимно перпендикулярны. Волны с
определенным направлением колебаний этих векторов называются поляризованными. изображена такая
поляризованная волна.
Приемный рупор с детектором принимает только
поляризованную в определенном направлении волну. Это можно обнаружить, повернув
передающий или приемный рупор на 90°. Звук при этом исчезает.
Поляризацию наблюдают, помещая между генератором и
приемником решетку из параллельных металлических стержней. Решетку
располагают так, чтобы стержни были горизонтальными или вертикальными. При
одном из этих положений, когда электрический вектор параллелен стержням, в них
возбуждаются токи, в результате чего решетка отражает волны, подобно сплошной
металлической пластине. Когда же вектор перпендикулярен стержням, токи в
них не возбуждаются и электромагнитная волна проходит через решетку.
Интерференция волн. Направим излучающий рупор на два металлических листа, расположенные рядом друг с другом под углом, чуть меньшим 180°. Передвигая
приемный рупор вокруг листов, мы обнаружим последовательное усиление и ослабление мощности
принимаемой волны.
Дифракция волн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя, как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Электромагнитные волны обладают следующими свойствами. Они поглощаются, отражаются, испытывают преломление, поляризуются. Последнее свойство свидетельствует о поперечности этих волн.
Прочитать можно на сайте Физика.ru https://www.fizika.ru/kniga/index.php?mode=proverjalka&theme=11&id=11090