Какие свойства действий позволяют утверждать что тождественно равны

ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 7 класс
- Алгебра
- Мордкович
- Номер 36.4

Назад к содержанию
Условие
Какие свойства действий позволяют утверждать, что тождественно равны выражения:
а) а + 7b и 7b + а;
б) (х + 4) + у и x + (4 + у);
в)m * 7n и 7nm;
г) 5(с + d) + 3 и 5с + 5d + 3?
Решение 1

Решение 2

Другие задачи из этого учебника
- 36.1
- 36.2
- 36.3
- 36.4
- 36.5
- 36.6
- 36.7
Поиск в решебнике
Популярные решебники
 ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
 ГДЗ по алгебре за 7 класс: Мордкович А.Г.
ГДЗ по алгебре за 7 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович, 2013г.
 ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 7 класс
- Алгебра
- Мордкович
- Номер 36.5

Назад к содержанию
Условие
Какие свойства действий позволяют утверждать, что тождественно равны выражения:
а) 2с * 4 и 8с;
б) (р — p)q и 0;
в) 4t + 8sr и 8rs + 4t;
г) (а + b) * 2 и 2а + 2b?
Решение 1

Решение 2

Другие задачи из этого учебника
- 36.2
- 36.3
- 36.4
- 36.5
- 36.6
- 36.7
- 36.8
Поиск в решебнике
Популярные решебники
 ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
 ГДЗ по алгебре за 7 класс: Мордкович А.Г.
ГДЗ по алгебре за 7 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович, 2013г.
 ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 7 класс
- Алгебра
- Макарычев
- Задание 85

Назад к содержанию
Условие
Какие свойства действий позволяют утверждать, что тождественно равны выражения:
а) ab + 16с и 16с + ab; в) ху + 3 и 3 + ху;
б) (а + 2) + х и а + (2 + x); г) 5(b + с) и 5b + 5с?
Решение 1
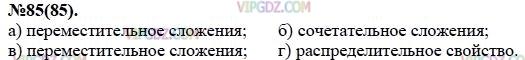
Решение 2

Решение 3

Другие задачи из этого учебника
- 82
- 83
- 84
- 85
- 86
- 87
- 88
Поиск в решебнике
Популярные решебники
 ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
 ГДЗ по алгебре за 7 класс: Мордкович А.Г.
ГДЗ по алгебре за 7 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович, 2013г.
 ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
Учебник для 7 класса
Алгебра
Найдём значения выражений 3(х + у) и Зх + Зу при х = 5, у = 4:
3(х + y) = 3(5 + 4) = 3 • 9 = 27,
3x + Зу = 3 • 5 + 3 • 4 = 15 + 12 = 27.
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х + у) и 3x + 3у равны.
Рассмотрим теперь выражения 2х + у и 2ху. При х = 1, у = 2 они принимают равные значения:
2х + у = 2 • 1 + 2 = 4,
2ху = 2 • 1 • 2 = 4.
Однако можно указать такие значения х и у, при которых значения этих выражений не равны. Например, если х = 3, у = 4, то
2х + у = 2 • 3 + 4 = 10,
2ху = 2 • 3 • 4 = 24.
Определение. Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Выражения 3(х + у) и Зх + Зу являются тождественно равными, а выражения 2х + у и 2ху не являются тождественно равными.
Равенство
3(x + у) = Зх + Зу
верно при любых значениях х и у. Такие равенства называются тождествами.
Определение.Равенство, верное при любых значениях переменных, называется тождеством*.
Тождествами считают и верные числовые равенства.
С примерами тождеств вы уже встречались. Так, тождествами являются равенства, выражающие основные свойства действий над числами:
а + b = b + а, (а + b) + с = а + (b + с),
ab = ba, (аb)с = а(bс),
а(b + с) = аЬ + ас.
Можно привести и другие примеры тождеств:
а + 0 = а, а + (-а) = 0, а — b = а + (-b),
а • 1 = а, а • (-b) = -ab, (-а)(-b) = аЬ.
Чтобы найти значение выражения ху — хz при заданных значениях х, у и z, надо выполнить три действия. Например, при х = 2,3, у = 0,8, z = 0,2 получаем
ху — хz = 2,3 • 0,8 — 2,3 • 0,2 = 1,84 — 0,46 = 1,38.
Этот результат можно получить, выполнив лишь два действия, если воспользоваться выражением х(у — z), тождественно равным выражению ху — хz:
х(у — z) = 2,3 (0,8 — 0,2) = 2,3 • 0,6 = 1,38.
Мы упростили вычисления, заменив выражение ху — хz тождественно равным выражением х(у — z).
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным, преобразова нием или просто преобразованием выражения.
Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.
Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач.
Некоторые тождественные преобразования вам уже приходилось выполнять, например приведение подобных слагаемых, раскрытие скобок. Напомним правила выполнения этих преобразований:
чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть;
если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки;
если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.
Пример 1. Приведём подобные слагаемые в сумме
5х + 2х — Зх.
Решение: Воспользуемся правилом приведения подобных слагаемых:
5х + 2х — Зх = (5 + 2 — 3)х = 4х.
Это преобразование основано на распределительном свойстве умножения.
Пример 2. Раскроем скобки в выражении
2а + (b — 3с).
Решение: Применим правило раскрытия скобок, перед которыми стоит знак «плюс»:
2а + (b — Зс) = 2а + b — Зс.
Проведённое преобразование основано на сочетательном свойстве сложения.
Пример 3. Раскроем скобки в выражении а — (4b — с).
Решение: Воспользуемся правилом раскрытия скобок, перед которыми стоит знак «минус»:
а — (4b — с) = а — 4b + с.
Выполненное преобразование основано на распределительном свойстве умножения и сочетательном свойстве сложения. Покажем это. Представим в данном выражении второе слагаемое -(4b — с) в виде произведения (-1)(4b — с):
а — (4Ь — с) = а + (-1)(4b — с).
Применив указанные свойства действий, получим
а — (4b — с) = а + (-1)(4b — с) = а + (-4b + с) = а — 4b + с.
Упражнения
- Какие свойства действий позволяют утверждать, что тождественно равны выражения:

- Являются ли тождественно равными выражения:

- Являются ли тождественно равными выражения:

- Какие свойства действий позволяют утверждать, что данное равенство является тождеством:

- Какое из данных равенств не является тождеством?

- Упростите выражение, используя переместительное и сочетательное свойства умножения:

- Упростите выражение:

- Преобразуйте выражение в тождественно равное, используя распределительное свойство умножения:

- Замените выражение тождественно равным, используя распределительное свойство умножения:

- Среди выражений 2(b — а), -2 (а — b), -2а — 2b, -2а + 2b найдите те, которые тождественно равны выражению 2b — 2а.
- Приведите подобные слагаемые:

- Приведите подобные слагаемые:

- Приведите подобные слагаемые:

- Раскройте скобки:

- Запишите без скобок выражение:

- Упростите выражение:

- Раскройте скобки и приведите подобные слагаемые:

- Упростите выражение и найдите его значение:

- Упростите выражение:

- Докажите, что при любом а значение выражения 3(а + 2) — 3a равно 6.
- Раскройте скобки и приведите подобные слагаемые:

- Упростите выражение и найдите его значение:

- Составьте выражение но условию задачи и упростите его:
а) У Игоря 3 альбома с марками. В первом альбоме а марок, во втором — на 15 марок больше, чем в нервом, а в третьем — втрое больше, чем во втором. Сколько марок в трёх альбомах?
б) Пётр приобрёл 8 билетов лотереи «Надежда» и 6 билетов лотереи «Удача». Билет лотереи «Удача» стоил а р., а лотереи «Надежда» был на 10% дороже. Найдите стоимость покупки.
- Сравните значения выражений, не вычисляя их:

Ответ запишите в виде неравенства.
- Техническое перевооружение цеха позволило выпускать в сутки 180 станков вместо 160. На сколько процентов повысился выпуск станков в сутки?
- Отметьте на координатной прямой точки, соответствующие числам:

Контрольные вопросы и задания
- Сформулируйте переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения.
- Какие выражения называются тождественно равными? Приведите пример тождественно равных выражений.
- Какое равенство называется тождеством? Приведите пример тождества.
*В дальнейшем понятия «тождественно равные выражения» и «тождество» будут уточнены.

