Какие свойства биологической ткани моделируют элементы эквивалентной схемы

Электрические свойства биологических тканей моделируются сочетанием элементов, обладающих омическими и емкостными свойствами. Эти свойства можно моделировать с помощью эквивалентных электрических схем. Рассмотрим три из них, рис. 17.
Схема I не совсем удовлетворительна, т.к. содержит бесконечно большое сопротивление постоянному току (емкость не проводит постоянный ток), чего не наблюдается в тканях организма. Поэтому при низкой частоте схема I даст существенные отклонения расчетных значений импеданса (полного сопротивления) от реального импеданса биоткани. В схеме // при увеличении частоты тока ω емкостное сопротивление стремится к нулю 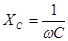 поэтому импеданс схемы также стремится к пулю. Это противоречит опыту.
поэтому импеданс схемы также стремится к пулю. Это противоречит опыту.
 У живых объектов импеданс уменьшается по мере увеличения частоты только до определенного значения. Для живых тканей характерно более сложное сочетание параллельного и последовательного соединений элементов, например, схема ///.
У живых объектов импеданс уменьшается по мере увеличения частоты только до определенного значения. Для живых тканей характерно более сложное сочетание параллельного и последовательного соединений элементов, например, схема ///.
В состоянии покоя реактивное сопротивление ткани носит только емкостный характер, при возбуждении ткань приобретает индуктивные свойства и обладает индуктивным сопротивлением
XС =ω L.
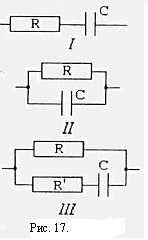
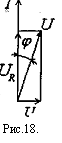 При анализе электрических свойств ткани рассматриваем только состояние покоя. Найдем импеданс Z простейшей эквивалентной электрической схемы /, рис. Векторная диаграмма имеет вид, показанный на рис.17. Общее напряжение равно
При анализе электрических свойств ткани рассматриваем только состояние покоя. Найдем импеданс Z простейшей эквивалентной электрической схемы /, рис. Векторная диаграмма имеет вид, показанный на рис.17. Общее напряжение равно
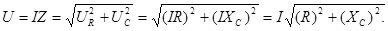
Следовательно, импеданс цепи равен
Угол сдвига фазы между током I и напряжением U найдем из условия.
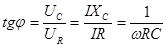
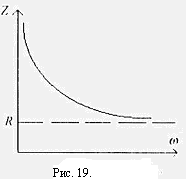 На рис.19. показана зависимость Z импеданса эквивалентной электрической схемы / (рис.17.) от частоты, построенная но формуле
На рис.19. показана зависимость Z импеданса эквивалентной электрической схемы / (рис.17.) от частоты, построенная но формуле 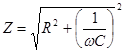
 Как видно из рис. 19., импеданс цепи монотонно падает с увеличением частоты электрического тока, постепенно приближаясь к активному сопротивлению R..
Как видно из рис. 19., импеданс цепи монотонно падает с увеличением частоты электрического тока, постепенно приближаясь к активному сопротивлению R..
Величины логарифмов импеданса и относительной диэлектрической проницаемости можно считать по модулю примерно пропорциональными друг другу.
Зависимость импеданса (или относительной диэлектрической проницаемости) биологических тканей от частоты электрического тока называется дисперсией импеданса (или относительной диэлектрической проницаемости), а график этой зависимости дисперсионной кривой.
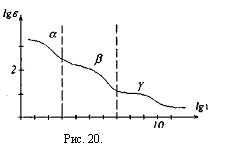
В отличие от зависимости импеданса от частоты электрического тока для эквивалентной электрической схемы биологической ткани, реальная дисперсионная кривая, например, скелетной мышцы, немонотонно падает с увеличением частоты, рис.20.
При действии на ткани организма переменного электрического тока или переменного электрического поля наблюдаются три области дисперсии. Область а — дисперсии.
Наблюдается до частот 1кГц (lgv≈3)
В низкочастотной части спектра области а- дисперсии электрический ток течет практически только по межклеточной жидкости, т.к. сопротивление мембран клеток очень велико. В высокочастотной части спектра импеданс падает за счет снижения емкостного сопротивления мембран клеток Хс = 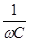 Возникает ток смещения, текущий через мембрану.
Возникает ток смещения, текущий через мембрану.
Область β- дисперсии.Наблюдается до частот I04 кГц (Igv≈3 – 7)
За счет увеличения частоты переполяризации мембран клеток снижается емкостное сопротивление ткани. Переполяризация рассматривается относительно пулевого уровня потенциала па мембране, за который принят потенциал покоя.
Затраты энергии на поляризацию и нереполяризацию клеточных структур (мембран, белковых молекул, молекул воды, атомов и т.д.) определяют импеданс ткани. Снижение этих затрат приводит к снижению импеданса биоткани.
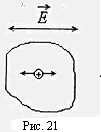 Многие ионы внутри клеток, рис.21, при такой частоте колебаний напряженности электрического поля
Многие ионы внутри клеток, рис.21, при такой частоте колебаний напряженности электрического поля  не успевают дойти до клеточных и внутриклеточных мембран. Для них сопротивление мембран роли не играет.
не успевают дойти до клеточных и внутриклеточных мембран. Для них сопротивление мембран роли не играет.
В высокочастотной области β- дисперсии существенное значение приобретает структурная поляризация и переполяризация крупных, в частности белковых молекул. Структурная поляризация заключается в том, что внутри молекулы, под действием электрического поля, смещаются ионы и ионные группы, входящие в состав молекул, что влияет на функциональные свойства белков.
Область γ дисперсии. Наблюдается до частот 107 кГц (Igv =• 7 — 10).
 За счет высокой частоты колебаний электрического тока, емкостное сопротивление мембран очень мало и они не представляют большого препятствия для переменного тока. Поэтому сопротивление биоткани в общем мало.
За счет высокой частоты колебаний электрического тока, емкостное сопротивление мембран очень мало и они не представляют большого препятствия для переменного тока. Поэтому сопротивление биоткани в общем мало.
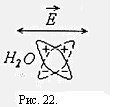
В низкочастотной части спектра области γ- дисперсии уменьшение диэлектрической проницаемости обусловлено постепенным ослаблением ориентационной переполяризации дипольных молекул воды, рис.22. В этой области важный вклад в импеданс ткани вносит структурная поляризация крупных молекул. Энергия электрического тока с увеличением частоты все меньше теряется на переориентацию молекул воды и структурную переполяризацию крупных молекул, поэтому уменьшается импеданс ткани.
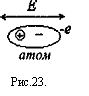
В высокочастотной части спектра γ — дисперсии молекулы воды под действием переменной напряженности Е почти не переполяризуются. Уровень электрического сопротивления определяется электронной переполяризацией атомов, т. с. возникновением переменных атомных диполей, рис.23.
Это
условная модель, которая характеризует
живую ткань, как проводник переменного
тока.
В
основе создания таких схем лежат три
положения:
1.содержимое
клетки и внеклеточная среда – это
проводники с ионной проводимостью. Они
обладают активным сопротивлением
внутриклеточной
– Rвн
и
внеклеточной (внешней) среды – Rср
2.клеточная
мембрана является диэлектриком. Но
здесь имеет место небольшая ионная
проводимость, а следовательно, есть
небольшое активное сопротивление
мембраны-Rм.
3.содержимое
клетки и внеклеточная среда, раздражаемые
мембраной, представляют собой конденсатор
определенной емкости (См).
При
построении эквивалентной схемы живой
ткани, например крови, необходимо
учитывать пути тока:
через
клеткув
обход клетки (через клеточную среду).











См
Rм




 Rср
Rср

Rкл











См
Rм
С
повышением частоты тока, емкостное
сопротивление уменьшается, а следовательно,
ток через конденсатор будет нарастать,
а общее сопротивление будет снижаться.
Вопрос
№3.
Особенности живой ткани как проводника переменного тока. Дисперсия электропроводимости и её количественная оценка.
Живая
ткань, как проводник переменного тока,
имеет следующие особенности:
1.полное
сопротивление живой ткани зависит от
её вида, физиологического состояния
(например, кровенаполнения) и от частоты
тока.
2.с
увеличением частоты полное сопротивление
живой ткани снижается нелинейно до
определенного значения, а затем становится
почти постоянным.
3.
сопротивление живой ткани переменному
току меньше, чем постоянному.
При
пропускании переменного тока через
живую ткань наблюдается дисперсия
электропроводимости — это зависимость
удельного сопротивления живой ткани
от частоты переменного тока.
Дисперсия
наиболее выражена в частотном диапазоне
от 10² до 10 Гц.
Для
мертвой ткани дисперсия отсутствует.
.
— удельное сопротивление
=
—- [Ом
∙ м² / м ]= [Ом · м ]
П остроим
остроим
график:


 живая
живая
ткань
 Мертвая
Мертвая
ткань

10²
10 ν,Гц
Метод,
основанный на изменении дисперсии
тканей от кровенаполнения и, следовательно,
от сердечно-сосудистой деятельности,
носит название реографии.
Для
количественной оценки дисперсии вводится
коэффициент дисперсии.
Это
безразмерная величина, равная отношению
удельного сопротивления при частоте
10² Гц к удельному сопротивлению при
частоте 10 Гц.
Кд=
/
Коэффициент
дисперсии для разных живых тканей
различен, например, для печени млекопитающих
он равен 10. У умирающей ткани. Кд стремится
к единице.
Вопрос
№ 4.
Соседние файлы в папке Медицинская физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полная цепь переменного тока — это цепь из генератора, а также R, C, и L элементов, взятых в разных сочетаниях и количествах.
Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи.
Последовательная цепь — это такая цепь, где все элементы могут быть соединены последовательно, один за другим.
В параллельной цепи R, C, L элементы соединены параллельно.
Особенности полной цепи:
1.Соблюдается закон Ома
2.Полная цепь оказывает переменному току сопротивление. Это сопротивление называется полным (мнимым, кажущимся) или импедансом.
3.Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и вычисляется не простым, а геометрическим (векторным) суммированием. Для последовательно соединенных элементов формула импеданса имеет следующее значение:
здесь:
Z — импеданс последовательной цепи,
R — активное сопротивление,
XL – индуктивное и XC – ёмкостное сопротивление,
L — индуктивность катушки (генри),
C — ёмкость конденсатора (фарад).
Так как ёмкостное и индуктивное сопротивления дают для напряжения сдвиг фаз в противоположном направлении, возможен случай, когда XL = XC. При этом алгебраическая сумма модулей будет равна нулю, а импеданс – наименьшим.
Состояние, при котором в цепи переменного тока ёмкостное сопротивление равно индуктивному, называется резонансом напряжения. Частота, при которой XL = XC, называется резонансной частотой. Эту частоту np можно определить по формуле Томсона:
4.Особенности импеданса живой ткани и её эквивалентная электрическая схема.
При пропускании тока через живую ткань, её можно рассматривать как электрическую цепь, состоящую из определенных элементов.
Экспериментально установлено, что это цепь обладает свойствами активного сопротивления и ёмкости. Это доказывается выделением тепла и уменьшением полного сопротивления ткани с возрастанием частоты. Свойств индуктивности у живой ткани практически не обнаруживается. Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.
Импеданс живой ткани можно рассматривать как для последовательного, так и для параллельного соединения её элементов.
При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:
Z_ — импеданс последовательной цепи,
R — её активное сопротивление,
XC — ёмкостное сопротивление.
При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:
Теоретические формулы импеданса живой ткани при параллельном и последовательном соединении её элементов от экспериментальных отличаются следующим:
1.При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.
2.При параллельной схеме эти измерения показывают конечное значение Z, хотя теоретически оно должно стремиться к нулю.
Эквивалентная электрическая схема живой ткани – это условная модель, приближенно характеризующаяживую ткань, как проводник переменного тока.
Схема позволяет судить:
1.Какими электрическими элементами обладает ткань
2.Как соединены эти элементы.
3.Как будут меняться свойства ткани при изменении частоты тока.
В основе схемы лежат три положения:
1.Внеклеточная среда и содержимое клетки есть ионные проводники с активным сопротивлением среды Rср и клетки Rк.
2.Клеточная мембрана есть диэлектрик, но не идеальный, а с небольшой ионной проводимостью, а, следовательно, и сопротивлением мембраны Rм.
3.Внеклеточная среда и содержимое клетки, разделённые мембраной, являются конденсаторами См определенной ёмкости (0,1 – 3,0 мкФ/см2).
Если в качестве модели живой ткани взять жидкую тканевую среду – кровь, содержащую только эритроциты, то при составлении эквивалентной схемы нужно учитывать пути электрического тока.
Их два:
1.В обход клетки, через внеклеточную среду.
2.Через клетку.
Путь в обход клетки представлен только сопротивлением средыRср.
Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.
Если заменить электрические характеристики соответствующими обозначениями, то получим эквивалентные схемы разной степени точности:
Схема Фрике (ионная проводимость не
учитывается).
Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)
Обозначения на схеме:
Rcp — активное сопротивление клеточной среды
Rk — Сопротивление клеточного содержимого
Cm — ёмкость мембраны
Rm — сопротивление мембраны.
Анализ схемы показывает, что при увеличении частоты тока проводимость клеточных мембран увеличивается, а полное сопротивление тканевой среды уменьшается, что соответствует практически проведенным измерениям.
Электрический ток может проходить через биологическую ткань двумя путями:
— через межклеточное пространство (жирные пунктирные линии) с сопротивлением Rср
— через межклеточное пространство с пересечением одной и нескольких клеток (тонкие пунктирные линии) с сопротивлением Rкл.
Для постоянного тока электрическая схема для двух указанных путей распространения тока чисто межклеточный и межклеточный с прохождением хотя бы через одну клетку выглядит следующим образом:
Схема А имеет существенное расхождение с опытными данными в области низких частот близких к нулю – величина импеданса неограниченно возрастает с уменьшением частоты.
Схема Б удовлетворительно описывает частотную зависимость величины импеданса на низких частотах, но в области высоких частот величина импеданса стремится к нулю, что не соответствует опытным данным.
Наилучшее согласие с экспериментом обеспечивает эквивалентная схема В: на низких частотах величина импеданса определяется сопротивлением R1, на высоких частотах — параллельными соединениями R1 и R2.
При w=0 импеданс цепочки равен R1 (конденсатор не проводит постоянный ток).
При wà «бесконечности» емкостное сопротивление стремится к нулю, а импеданс к значению, которое соответствует соединения резисторов R1 и R2:
При увеличении частоты импеданс плавно уменьшается. Но для реальных биологических тканей эта зависимость сложнее.
ИМПЕДАНС ТКАНЕЙ ОРГАНИЗМА
Импеданс биологических тканей имеет комплексный характер. Активная составляющая импеданса (R) обусловлена проводимостью жидких сред организма, которые являются электролитами. Реактивная составляющая (Х) определяется емкостными свойствами ткани.
Абсолютная величина импеданса рассчитывается в этом случае по формуле:
Фазовый сдвиг ( ) определяет соотношение активной и реактивной составляющей импеданса.
В случае переменного тока следует ожидать существование зависимости полного электрического сопротивления (импеданса) живой ткани от частоты. Поскольку путь электрического тока возможен через внеклеточную среду и через клетку, необходимо учитывать емкостную составляющую клеточной мембраны.
В общем случае органическую ткань можно рассматривать как клетки, находящиеся в проводящей среде (R1), роль которой играет, например, межклеточная жидкость. Клеточные мембраны обладают емкостными свойствами, а электролиты внутри клетки обладают активным сопротивлением (R2).
ДИСПЕРСИЯ ИМПЕДАНСА
На графике проявляются три интервала частот, в которых величина медленно меняется с частотой по сравнению с общим ходом кривой. Они называются областями –альфа ( ), бета ( ) и -гамма ( ) дисперсии соответственно. Им соответствуют три области частот:
— низкие частоты
— радиочастоты
— микроволновые частоты
Наличие этих областей с частотной дисперсией диэлектрической проницаемости (e=f(v)), от которой зависит величина емкости.
- Альфа – дисперсия:обусловлена поляризацией целых клеток в результате диффузии ионов, что требует относительно большого времени, поэтому данный механизм проявляется при действии электрического поля низкой частоты. В этой области емкостное сопротивление мембран велико и преобладают тока, протекающие через растворы электролитов, окружающие фрагменты мембран. Поляризация клеток – самый медленный процесс среди всех механизмов поляризации. При увеличении частоты поляризация клеток практически полностью прекращается
- Бета – дисперсия:обусловлена структурной поляризацией клеточных мембран, в которой участвуют белковые макромолекулы, а на её верхней границе – глобулярные водорастворимые белки, фосфолипиды и мельчайшие субклеточные структуры. При этом получаются существенно меньшие значения диэлектрической проницаемости, чем поляризация целых клеток. Этот механизм поляризации доминирует на частотах 1-10 МГц. При увеличении частоты перестает работать.
- Гамма – дисперсия:обусловлена процессами ориентационной поляризации молекул свободной и связанной воды, а также низкомолекулярных веществ типа сахаров и аминокислот. При этом диэлектрическая проницаемость уменьшается еще больше. Этот механизм поляризации доминирует на частотах выше 1 ГГц.
19. Физические основы электрокардиографии. Дипольный электрический генератор (токовый диполь). Электрическое поле диполя. Основы теории отведений Эйнтховена. Электрокардиограмма.
Электрокардиография (ЭКГ) — регистрация на поверхности тела биопотенциалов, возникающих в результате возбуждения сердечной мышцы.
ФИЗИЧЕСКИЙ ПОДХОД К ЭКГ: создать (выбрать) модель электрического генератора, которая соответствует регистрируемым потенциалам тела человека.
Дипольный электрический генератор (токовый диполь) в вакууме или диэлектрике сохраняется очень долго; в проводящей среде под действием электрического поля диполя возникает движение свободных зарядом и диполь ослабляется; если источник тока поместить в проводящую среду, то клеммы источника будут полюсами диполя, заряды будут стекать с полюсов такого диполя, но диполь будет сохраняться в проводящей среде за счёт притока новых зарядов от их химического генератора.
РИСУНОК:
Токовый диполь — это двухполюсная система в бесконечной проводящей среде, состоящая из истока (положительный электрод) и стока (отрицательный электрод).
Дипольный момент:
Дипольный момент — вектор, направленный от стока (-) к истоку (+).
Потенциал, создаваемый токовым диполем в точке А, удалённой от него на расстояние r>>L:
Где y – удельная электропроводность; она характеризует проводящие свойства среды.
Физические основы ЭКГ.
Сердце человека – мощная мышца. При синхронном возбуждении множества волокон сердечной мышцы, в среде течет ток , который даже не поверхности тела создает разности потенциалов порядка нескольких мВ. Эта разность потенциалов регистрируется при записи электрокардиограммы.
Теория Эйнтховена
«Сердце есть токовый диполь с дипольным моментом «Pт», который поворачивается, изменяет своё положение и точку приложения за время сердечного цикла».
Сердце располагается в центре равностороннего треугольника, вершинами которого являются правая рука, левая рука и левая нога. Поэтому разности потенциалов, снятые между этими точками, суть проекции дипольного момента сердца на стороны этого треугольника. Эти разности потенциалов называют «отведениями»:
· Отведение I – правая рука — левая рука
· Отведение II – правая рука – левая нога
· Отведение III – левая рука – левая нога
Им соответствуют разности потенциалов U1, U2, U3. Соотношения между разностью потенциалов получены как соотношения проекций вектора Pc на стороны треугольника:
U1:U2:U3=Pc1:Pc2:Pс3
Так как электрический момент диполя – сердца изменяется со временем, то в отведении будут получены временные зависимости напряжения – электрокардиограммы.
1) Сердце на больших расстояниях создает поле, подобное полю токового диполя
2) Интегральный электрический вектор сердца ( ) находится в однородной проводящей среде, т.е. тело — однородная проводящая среда.
3) Вектор располагается в центре равностороннего треугольника, начало дипольного момента неподвижно
Электрокардиограмма — это временная зависимость изменения разности потенциалов.
· зубец P — предсердный комплекс;
· интервал PQ — время прохождения возбуждения по предсердиям до миокарда желудочков;
· комплекс QRS — желудочковый комплекс;
· зубец q — возбуждение левой половины межжелудочковой перегородки;
· зубец R — основной зубец ЭКГ, обусловлен возбуждением желудочков;
· зубец s — конечное возбуждение основания левого желудочка (непостоянный зубец ЭКГ);
· сегмент ST — соответствует периоду сердечного цикла, когда оба желудочка охвачены возбуждением;
· зубец T — регистрируется во время реполяризации желудочков;
· интервал QT — электрическая систола желудочков;
· зубец u — клиническое происхождение этого зубца точно неизвестно (регистрируется не всегда);
· сегмент TP — диастола желудочков и предсердий.
