Какие свойства бинарных отношений

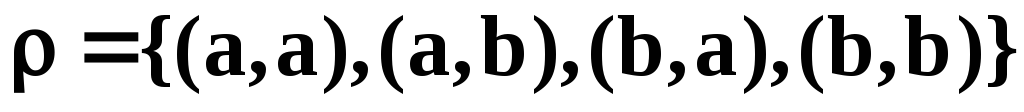
Бинарные отношения в общем случае обладают свойствами рефлексивности, антирефлексивности, симметричности, антисимметричности, транзитивности, связности.

1. Рефлексивное отношение – отношение , в котором для любого выполняется

Другая запись такого отношения .

Главная диагональ матрицы такого отношения содержит только единицы.

Примером рефлексивного отношения является отношение «подобие треугольников, заданное на множестве всех треугольников евклидовой плоскости»: каждый треугольник подобен себе самому;

— отношения « » и «иметь общий делитель».

2. Антирефлексивное отношение – отношение , в котором ни для какого не выполняется

или .

Главная диагональ матрицы такого отношения содержит только нули.

Примером антирефлексивного отношения является отношение «перпендикулярность прямых, заданных на множестве всех прямых евклидовой плоскости»:

— никакая прямая не перпендикулярна себе самой;

— отношения «<» и «быть сыном».

Отношение «быть симметричным относительно оси » не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси и несимметрична сама себе в противном случае.

3. Симметричное отношение – отношение , в котором для пары

из следует или .

Иначе говоря, для любой пары отношение симметричности выполняется либо в обе стороны, либо не выполняется вообще. Матрица симметричного отношения симметрична относительно главной диагонали: для любых и . Для симметричного отношения .

Примером симметричного отношения является отношение «быть симметричным относительно оси », которое является симметричным: если первая точка симметрична второй, то и вторая симметрична первой;

отношение «проживать в одном доме», заданное на множестве всех жителей некоторого города: если живет в одном доме с , то живет в одном доме с .

4. Антисимметричное отношение – отношение ,в котором для

пары из и следует, что или

Примером антисимметричного отношения является отношение « », заданное на множестве действительных чисел: действительно, если , и , то .

5. Транзитивное отношение – отношение ,в котором для любых

из и следует или

Примером транзитивного отношения являются отношения «равенство», « », «жить в одном городе»: действительно если ; если ; если и живут в городе и и живут в городе , то и также живут в городе .

Отношение «быть сыном» нетранзитивно: если является сыном и является сыном то это не значит, что является сыном . Отношение «пересекаться», то есть «иметь непустое пересечение», заданное на системе множеств, также нетранзитивно. Например, пересекается с , пересекается с , однако и не пересекаются.

Транзитивное замыкание отношения. Транзитивное замыкание отношения – это отношение , которое определяется следующим образом: , если в существует цепочка из элементов , в которой между соседними элементами выполнено отношение : .

Если транзитивно, то . Действительно, если , то(цепочка состоит из двух элементов и ), поэтому . Если же , тосуществует цепочка . Но так как транзитивно, то , поэтому . Из включения в обе стороны следует .

Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком», являющееся объединением отношений «быть сыном», «быть внуком», «быть правнуком» и т.д. Транзитивным замыканием отношения «иметь общую стену» для жильцов дома является отношение «жить на одном этаже».

6. Связное (полное) отношение – отношение , в котором для пары

из следует или ,

или .

Примером связного (полного) отношения является отношение «быть старше», заданное на множестве родных братьев и сестер некоторой семьи: если , то либо старше , либо старше .

Рассмотренные свойства можно определить с помощью выражений:

1. , 2. , 3. , 4. ,

5. (где – композиция отношений), 6. .

Если даны два отношения и , то операции над этими отношениями сводятся к операциям над ними, аналогичные операциям над множествами:

объединению ; пересечению ; разности ; симметрической разности . Дополнение отношения ( ) будет равно .

На основании приведенных выше свойств отношений можно дать им ряд определений.

Отношение частичного порядка – отношение, которое рефлексивно, антисимметрично и транзитивно.

Отношение линейного порядка – отношение частичного порядка, которое связно.

Отношение строгого порядка – отношение, которое антирефлексивно, антисимметрично и транзитивно.

Отношение строгого линейного порядка – связное отношение строгого порядка.

В теории множеств важную роль играют два вида специальных бинарных отношений: эквивалентности и порядка, прообразами которых являются понятия равенства, предшествования и предпочтения.

Источник

Пусть
задано на множестве,
.

1.
Рефлексивность:

Отношение на
множествеXназываетсярефлексивным, если для любогоимеет место,
то есть каждый элемент находится в
отношениик
самому себе.

Матрица рефлексивного отношения имеет
единичную главную диагональ, а граф
рефлексивного отношения – имеет петлю
возле каждого своего элемента.

Например:

На множестве людей: “быть родственником”,
”обучаться в одной студенческой группе
”.

На множестве множеств: AB, A=B.

2. Антирефлексивность: .

Отношение на
множествеXназываетсяантирефлексивным, если не
существуеттакого, чтоимеет место,
то есть ни один элемент не находится
в отношениик самому себе.

Матрица антирефлексивного отношения
имеет нулевую главную диагональ, а граф
– не имеет ни одной петли.

Например:

На множестве людей: “быть родителем”,
”быть ребенком”.

На множестве множеств: AB, AB.

3. Нерефлексивность:.

4. Симметричность: .

Отношение на
множествеXназываетсясимметричным, если для всехииз Х, из принадлежности(x,y)
отношениюследует, чтои
принадлежит отношению.

Матрица симметричного отношения
симметрична относительно главной
диагонали, а граф – для
каждой дуги (x,y)
существует обратная дуга(y,x).

Какие свойства бинарных отношений

Например:

На множестве людей: “быть родственником”,
”обучаться в одной студенческой группе
”. Отношение
«брат»
является симметричным
на множестве
мужчин и не является
симметричным на
множествевсех людей.

На множестве множеств:
,.

5. Антисимметричность: .

Отношение на
множествеXназываетсяантисимметричным, если для всехииз Х, из принадлежности(x,y)
и(y,x)
отношениюследует, что.

Матрица антисимметричного отношения
не имеет ни одной симметричной единицы
относительно главной диагонали, а граф
– длякаждой
дуги (x,y)
не существует
обратная дуга(y,x)
и наоборот.

Какие свойства бинарных отношений

Свойства симметричности и антисимметричности
не являются взаимоисключающими, примером
может служить отношения равенства на
множестве натуральных чисел.

Например:

На множестве людей: “быть выше”, ”быть
равным”.

На множестве множеств:
,,.

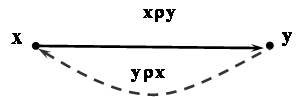
6. Транзитивность: .

Отношение
на множественазываетсятранзитивным, если для
всехизмножества
,из принадлежностииотношениюследует, чтотакже принадлежит.

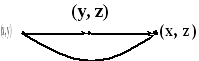
Какие свойства бинарных отношений

Например:

На множестве людей: “быть выше”,
”обучаться в одной студенческой группе”.

На множестве множеств:
,
,
.

Отношение rна множестве Xнеявляется
транзитивным,если
существует, хотя бы один пример того,что для некоторых х,y,zмножества Х
из принадлежности (x,y)
и(y,z)
отношениюrне
следует,что (x,z)такжепринадлежитr.

Например.

1)
.

Отношение неявляется
транзитивным,потому что
из принадлежности этому отношению пар
и,
неследует,что
и парапринадлежит
отношению .

2) Пусть задано двухэлементное
множество определим
все бинарные отношения на этом множестве:
.
Для всех отношений, заданных на множестве
,
определить наличие или отсутствие
основных свойств.

Введем следующие обозначения:

а) рефлексивность– Р;

б) антирефлексивность– АР;

в) симметричность– С;

г) антисимметричность– АС;

д) транзитивность– Т.

№	Р	АР	С	АС	Т
1	—	+	+	+	+
2	—	—	+	+	+
3	—	+	—	+	+
4	—	+	—	+	+
5	—	—	+	+	+
6	—	—	—	+	+
7	—	—	—	+	+
8	+	—	+	+	+
9	—	+	+	—	—
10	—	—	—	+	+
11	—	—	—	+	+
12	—	—	+	—	—
13	+	—	—	+	+
14	+	—	—	+	+
15	—	—	+	—	—
16	+	—	+	—	+

Отношение порядка– антисимметрично,
транзитивно.

Отношение нестрого порядка()
– рефлексивно,
антисимметрично,

транзитивно.

Например:

На множестве множеств:
,.

Отношение строгого порядка()
– антирефлексивно,
антисимметрично,

транзитивно.

Например:

На множестве множеств: “”.

— “xпредшествуетyв смысле
отношения строгого порядка”,

— “xпредшествуетyв смысле
отношения нестрогого
порядка”.

Два элементаи
некоторого упорядоченного множества
(множества, на котором существует
отношение порядка) сравнимы
между собой, если

предшествует
,
и/или
предшествует
в смыслеотношения
порядка.

Если в упорядоченном множестве
существует пара элементов xиy,
для которойни
непредшествует
,
ни
не предшествует
,
тогда говорят, что эти два элементанесравнимы
между собой в смысле этого.

В отношениях полногопорядка все
элементы сравнимы между собой, а в
отношенияхчастичногопорядка не
все элементы сравнимы между собой.

Например:

Отношения полного порядка:

Отношения частичного порядка:

на множестве множеств:
,
,.

Отношение эквивалентности( 
) – рефлексивно,

симметрично,

транзитивно.

Класс эквивалентностидля элемента:.

Например:

На множестве людей: “иметь
одно имя”, ”обучаться в
одной студенческой группе”.

На множестве множеств:
.

Отношение эквивалентности
разбивает
–множество,
на котором задано отношение нанепересекающиеся, которые
называют классами эквивалентности.

Элементы, принадлежащие
одному классу, находятсямежду собой в отношении
эквивалентности, элементы из разных
классов в отношении эквивалентности
между собой не находятся.

Например:

Отношение
задано на множествесписком пар.

Область определения:
.

Область значений:
.

Отношение
– рефлексивно, симметрично, транзитивно,
следовательно, это отношение
эквивалентности.

Классы эквивалентности:

Например:

Отношение .

Это отношение называют отношением
сравнения по модулюна множестве натуральных чисел.

означает, чтоиимеют одинаковый остаток при делении
на.

Отрезок натурального ряда
.

Отношение сравнения по модулю 3 на
:

Область определения и область значений:

Отношение
– рефлексивно, симметрично, транзитивно.

Отношение
– отношение эквивалентности.

Классы эквивалентности:
.

Пусть

–некоторое
бинарное отношение.

Обратным отношением называется отношение, которое
определяется следующим образом:

Обратное отношение получается путём
перестановки значений в парах исходного
отношения.

Пусть
и– произвольные бинарные
отношения такие, чтогде– некоторые множества.

Композиция отношений

и
– это таке
бинарное отношение которое состоит из
упорядоченных пар
для которых существует
такой элемент, что выполняются
условия:

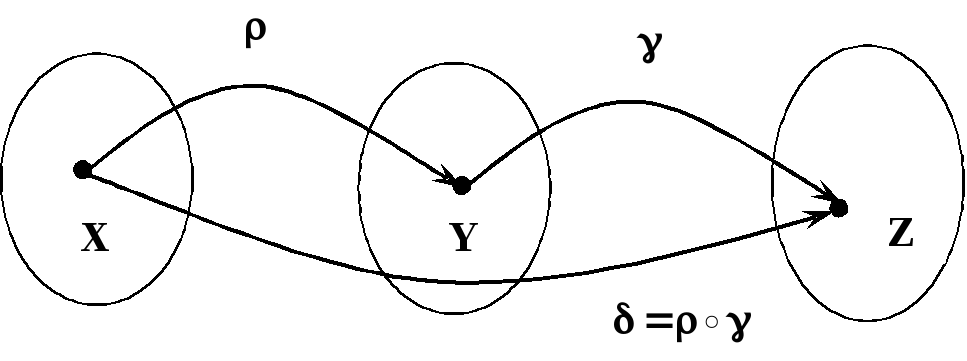
Какие свойства бинарных отношений

Например.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Рассмотрим отношение «уважать», определенное на множестве всех людей %%M%%. Для полной информации о том, кто кого уважает, составим следующее множество %%R%%. Переберем все пары %%(a, b)%%, где %%a, b%% пробегают множество всех людей. Если %%a%% уважает %%b%%, то пару %%(a,b)%% отнесем к множеству %%R%%, иначе — нет.

Этот список полностью отражает отношение «уважать». Если нужно узнать, уважает ли человек %%a%% человека %%b%%, то просмотрим множество %%R%%. Если пара %%(a, b) in R%%, то заключаем, что %%a%% уважает %%b%%. В случае %%(a,b) notin R%% — %%a%% не уважает %%b%%.

Определение

Бинарным отношением, определенным на множестве %%M%%, называется произвольное подмножество %%R%% из декартового произведения %%M^2%%.

Пример

Рассмотрим отношение больше на множестве %%M = {1, 2}%%. Тогда

$$
M^2 = big{(1, 1), (1,2), (2,1), (2,2)big}
$$
Из него выбирем все пары %%(a,b)%%, где %%a > b%%. Получим
$$
R = big{(2,1)big}
$$

Виды бинарных отношений

Рефлексивное бинарное отношение

Бинарное отношение %%R%% на множестве %%M%% называется рефлексивным,
если для любого элемента %%a%% из %%M%%, выполняется условие %%a~R~a%%.
$$
begin{array}{l}
forall ain M~~a~R~a text{ или}\
forall ain M~~(a,a) in R.
end{array}
$$

Примеры

Рассмотрим отношение больше на множестве действительных чисел. Является ли отношение больше рефлексивным? Если да, то каждое число является больше самого себя, что неверно. Поэтому отношение больше не рефлексивно.
Рассмотрим отношение равно на множестве действительных чисел. Оно является рефлексивным, так как каждое действительное число равно самому себе.

Симметричное бинарное отношение

Бинарное отношение %%R%% на множестве %%M%% называется симметричным,
если для любых двух элементов %%a, b%% из %%M%%, из условия %%a~R~b%% следует условие %%b~R~a%%.

$$
begin{array}{l}
forall a,bin M~~a~R~b rightarrow b~R~a text{ или}\
forall a,bin M~~(a,b) in R rightarrow (b,a) in R.
end{array}
$$

Примеры

Рассмотрим отношение больше на множестве действительных чисел. Является ли отношение больше симметричным? Оно не является симметричным, так как если %%a > b%%, то условие %%b > a%% не выполняется. Поэтому отношение больше не симметрично.
Пусть %%R%% — отношение, определенное на множестве %%M = {a,b,c}%%. При этом %%R = big{ (a,b), (b,c), (a,a), (b,a), (c,b)big}%%. Для этого отношения имеем %%forall x,y in M ~~ (x,y) in R rightarrow (y,x) in R%%. По определению %%R%% симметрично.

Транзитивное бинарное отношение

Бинарное отношение %%R%% на множестве %%M%% называется транзитивным,
если для любых элементов %%a, b, c%% из %%M%%, из условий %%a~R~b%% и %%b~R~c%% следует условие %%a~R~c%%.

$$
begin{array}{l}
forall a,b,cin M~~a~R~b land b~R~c rightarrow a~R~c text{ или}\
forall a,b,cin M~~(a,b) in R land (b,c) in R rightarrow (a,c) in R.
end{array}
$$

Пример

Рассмотрим отношение больше на множестве дейтсвительных чисел. Оно является транзитивным, так как для любых элементов выполняется условние %%forall a,b,cin M~~a > b land b > c rightarrow a > c%%. Так, например, подставив вместо %%a, b%% и %%c%% числа %%2, 1%% и %%0%% соответственно, получим: если %%2 > 1%% и %%1 > 0%%, то %%2 > 0%% — верное утверждение (вспомните импликацию, из истины следует истина).

Антисимметричное бинарное отношение

Бинарное отношение %%R%% на множестве %%M%% называется антисимметричным,
если для любых элементов %%a, b%% из %%M%%, из условий %%a~R~b%% и %%b~R~a%% следует условие %%a = b%%.

$$
begin{array}{l}
forall a,b,cin M~~a~R~b land b~R~a rightarrow a = b text{ или}\
forall a,bin M~~(a,b) in R land (b,a) in R rightarrow a = b.
end{array}
$$

Пример

Отношение больше или равно на множестве действительных чисел антисимметрично. Действительно, если %%a geq b%% и %%b geq a%%, %%a = b%%.

Эквивалентное бинарное отношение

Бинарное отношение %%R%% на множестве %%M%% называется отношением эквивалентности,
если оно рефлексивно, симметрично и транзитивно.

Нетрудно проверить, что отношение параллельности на множестве прямых плоскости является отношением эквивалентности.

Отношение частичного порядка

Бинарное отношение %%R%% на множестве %%M%% называется отношением частичного порядка,
если оно рефлексивно, антисимметрично и транзитивно.

Отношение больше или равно на множестве действительных чисел является отношением частичного порядка.

Построение отрицаний

Пусть %%R%% — бинарное отношение на множестве %%M%%, и %%P%% — одно из следующих условий:

отношение %%R%% рефлексивно,
отношение %%R%% симметрично,
отношение %%R%% транзитивно,
отношение %%R%% антисимметрично.

Построим для каждого из них отрицание выполнения условия %%P%%.

Отрицание рефлексивности

По определению %%R%% рефлексивно, если каждый элемент множества %%M%% находится в отношении %%R%% к самому себе, то есть %%forall a in M~~a~R~a%%. Тогда рассмотрим отрицание рефлексивности как истинное высказывание %%overline{forall a in M~~a~R~a}%%. Используем равносильность %%overline{forall x P(x)} equiv exists x overline {P(x)}%%. В нашем случае получаем %%forall a in M~~a~R~a equiv exists ain M~~a~nottext{R }~a%%, что и нужно.

Аналогично получаем и остальные отрицания. В итоге получаем следующие утверждения:

%%R%% не рефлексивно тогда и только тогда, когда
$$
exists a in M~~a~not R~a
$$
%%R%% не симметрично тогда и только тогда, когда
$$
exists a, b in M~~ a~R~b land b~not R~a
$$
%%R%% не транзитивно тогда и только тогда, когда
$$
exists a, b, c in M a~R~b land b~R~c land a~not R~c
$$
%%R%% не антисимметрично тогда и только тогда, когда
$$
exists a, b in M~~ a~R~b land b~R~a land a neq b.
$$

Источник

Способы задания бинарного отношения

Определение бинарного отношения

Бинарные отношения

Пусть среди трех людей: Андрей (А), Василий (В) и Сергей (С) двое знакомы друг с другом (Андрей и Василий) и знают третьего – Сергея, но Сергей их не знает. Как описать отношения между этими людьми?

Имеем исходное множество Х = {А, В, С}. Далее из элементов множества Х составим упорядоченные пары:
(А, В), (В, А), (А, С), (В, С). Это множество пар и описывает связи между элементами множества X. Кроме того, множество этих пар есть подмножество декартова произведения X ´ X.

Определение. На множестве X задано бинарное отношение R, если задано подмножество декартова произведения X ´ X (т. е. R Ì X ´ X).

Пример 1. Пусть X = {1, 2, 3, 4}. Зададим на X следующие отношения:

Т = {(х, у) | х, у Î Х; х = у} – отношение равенства;

Р = {(х, у) | х, у Î Х; х = у — 1} – отношение

предшествования;

Q = {(х, у) | х, у Î Х; х делится на у} – отношение

делимости.

Все эти отношения заданы с помощью характеристического свойства. Перечислим элементы этих отношений для заданного множества X = {1,2,3,4}:

Т = {(1,1), (2,2), (3,3), (4,4)};

P = {(1,2), (2,3), (3,4) };

Q = {(4,4), (4,2), (4,1), (3,3), (3,1), (2,2), (2,1), (1,1)}.

Тот факт, что пара (х, у) принадлежит данному отношению R, будем записывать: (х, у) Î R или xRy. Например, для отношения Q запись 4Q2 означает, что 4 делится на 2 нацело, т. е. (4,2) Î Q.

Областью определения Dr бинарного отношения R называется множество DR = {x | (х, у) Î R}.

Областью значений ЕR бинарного отношения R называется множество ЕR = {у| (х, у) Î R}.

В примере для отношения Р областью определения является множество DR = {1,2,3}, а областью значений является множество ЕR = {2,3,4}.

Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения.

График отношения изображается в декартовой системе координат: на горизонтальной оси отмечается область определения, на вертикальной — область значений отношения. Элементу отношения (х, у) соответствует точка плоскости с этими координатами.

a б

Рис. 1.8. График отношения Q (а) и схема отношения Q (б)

Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (х, у) принадлежит отношению R, то соответствующие точки из DR и ЕR соединяются прямой.

Граф отношения R Ì X ´ X строится следующим образом. На плоскости в произвольном порядке изображаются точки — элементы множества X. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х, у) принадлежит отношению R.

Матрица отношения R Ì X ´ X – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества X. На пересечении строки х и столбца у ставится 1, если пара (х, у) Î R; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй – номеру столбца.

Пусть X = {х1, х2, …, хn} . Тогда матрица отношения
R Ì X ´ X имеет n строк и n столбцов, а ее элемент rij определяется по правилу:

1, если (xi, yj) Î R, где i = l, 2, …, n; j = l, 2, …, n.

0, если (xi, yj) Ï R.

Рис. 1.9. Граф отношения Q (а) и матрица отношения Q (б)

1. Отношение R на множестве X называется рефлексивным, если для всех х Î X выполняется условие (х, х) Î R. Отношение R на множестве Х называется нерефлексивным, если условие (х, х) Î R не выполняется хотя бы при одном х Î X .

2. Отношение R на множестве X называется симметричным, если из условия (х, у) Î R следует
(у, х) Î R. Отношение R на множестве X называется несимметричным, если для любых х, у Î X из условия (х, y) Î R следует (у, х) Ï R.

3. Отношение R на множестве X называется транзитивным, если для любых х, у, z Î R из одновременного выполнения условий (x, y) Î R и (у, z) Î R следует (х, z) Î R .

Пример. Рассмотрим следующие отношения на множестве X = {1,2,3,4,5,6,7}:

G = {(x, y) | х, у Î Х; х > у};

L = {(х, у) | х, у Î Х; х £ у};

M = {(x, y) | х, у Î X; (х — у) делится на 3};

К = {(х, y) | х, у Î Х; х2 + у2 £ 20}.

Исследуем, какими свойствами они обладают.

Среди приведенных в примере отношений рефлексивнымиявляются отношение L (т. к. х £ х справедливо при всех х Î X) и отношение М (т. к. х — х = 0 делится на 3, поэтому пара (х, х) принадлежит отношению М при всех х Î X).

Симметричными являются отношения М (если х — у делится на 3, то и у — х делится на 3) и К (если х2 + у2 £20, то и у2 + х2 £ 20).

Транзитивными являются отношения G, L, М.

Источник