Какие прямые уровня и свойства их проекций вы знаете
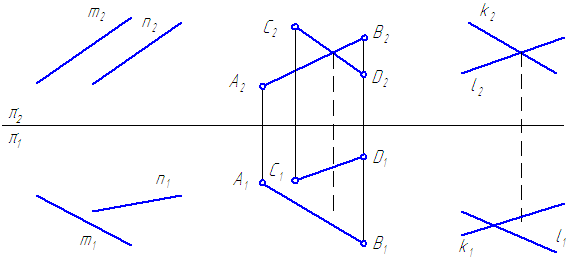
Положение прямой линии в пространстве вполне определяется двумя ее любыми точками. В общем случае проекцией прямой является прямая, в частном случае — точка, если прямая перпендикулярна плоскости проекций. Для построения проекций прямой достаточно иметь либо проекции двух ее точек, либо проекцию одной точки прямой и направление прямой в пространстве.
По своему расположению в пространстве относительно плоскостей проекций прямые линии разделяют на прямые общего положения, уровня и проецирующие.
2.2.1. Прямые общего положения.Это прямые, не параллельные и не перпендикулярные к плоскостям проекций. Проекции А1В1, А2В2 и А3В3 отрезка АВ прямой АВ общего положения (рис. 2.18, а) наклонены под острыми углами к осям x12, y13 и z23. Длины проекций отрезков этой прямой всегда меньше самого отрезка. Трехкартинный комплексный чертеж отрезка прямой общего положения, построенный по двум точкам А и В, показан на рис.2.18, б.
2.2.2. Прямые уровня. Это прямые, параллельные одной из плоскостей проекций — П1, П2 или П3. Следовательно, имеем три вида прямых уровня:
1) горизонтальная уровня a (горизонталь), параллельная П1 (прямая a с отрезком AB на ней на рис. 2.19, а, б);
2) фронтальная уровня (фронталь), параллельная П2 (прямая b c отрезком CD на ней на рис. 2.20, а);
3) профильная уровня, параллельная П3 (прямая с с отрезком ЕF на ней на рис. 2.20, б). На рис. 2.20 наглядные изображения прямых b и c относительно плоскостей проекций не показаны.
Одноименные проекции отрезков прямых уровня проецируются в натуральную величину, а разноименные параллельны осям, отделяющим их от одноименных. При этом для горизонтали одноименная проекция — горизонтальная, а разноименные — фронтальная и профильная и т. п.
Углы наклона прямых уровня a, b и c к плоскостям проекций П1, П2 и П3принято обозначать соответственно α, β и γ (на рис. 2.19 углы α, β и γ не показаны).
2.2.3. Проецирующие прямые.Это прямые, перпендикулярные к одной из плоскостей проекций и параллельные двум другим. Следовательно, имеем три вида проецирующих прямых:
1) горизонтально-проецирующая прямая, перпендикулярная П1 (прямая а с отрезком AB на ней на рис. 2.21, а);
2) фронтально-проецирующая прямая, перпендикулярная П2 (прямая b с отрезком CD на ней на рис. 2.21, б);
3) профильно-проецирующая прямая, перпендикулярная П3 (прямая c с отрезком EF на ней на рис. 2.21, в).
На рис. 2.21 в скобки заключены проекции невидимых точек. Вопрос определения видимости точек на проекциях подробнее будет рассмотрен ниже в п. «Скрещивающиеся прямые».
У проецирующих прямых одноименные проекции представляют собой точки, что вытекает из существа проецирующей прямой, вдоль которой ведется проецирование.
Каждая разноименная проекция проецирующей прямой перпендикулярна оси, отделяющей ее от одноименной проекции, а разноимённая проекция отрезка, расположенного на прямой уровня, является натуральной величиной этого отрезка.
2.2.4. Определение натуральной величины отрезка прямой общего положения.Натуральную величину прямой частного положения можно сразу определить на комплексном чертеже этой прямой.
Для определения натуральной величины отрезка прямой общего положения можно применить рассмотренный ранее (см. п. 2.1.2) способ замены плоскостей проекций. На рис.2.22 показано определение натуральной величины (Н.В.) отрезка AB прямой общего положения и определение углов наклона его к Π1 ( угол α) и к Π2 ( угол β) этим способом.
Дополнительная плоскость Π4проведена параллельноAB (х14||A1B1). Прямая AB преобразована в положение фронтали, следовательно A4B4 – натуральная величина AB.
Проведя дополнительную плоскостьΠ5||AB (х25||A2B2), также можно определить натуральную величинуAB. A5B5 – натуральная величинаAB. Прямая AB в системе Π2—Π5 стала горизонталью.
На рис.2.23 показано определение натуральной величины ABметодом треугольника.Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – алгебраическая разность расстояний его концов от плоскости Π1(ΔZ).
2.2.5. Взаимное положение прямых.Прямые линии в пространстве могут быть параллельными, пересекаться и скрещиваться.
Параллельные прямые. Из свойств параллельных проекций следует, что если прямые в пространстве параллельны, то все три пары их одноименных проекций параллельны. Очевидно и обратное положение: если одноименные проекции прямых параллельны, то прямые в пространстве параллельны.
Для определения параллельности прямых в общем случае достаточно параллельности двух пар одноименных проекций. В случае, если определяется параллельность линий уровня, то одной из двух пар параллельных проекций должна быть проекция на одноименную плоскость.
На рис. 2.24 показаны проекции параллельных прямых a и b общего положения, где a1║ b1 и a2║ b2. На рис. 2.25 показаны две горизонтали c и d. У горизонталей фронтальные и профильные проекции всегда параллельны осям, отделяющих их от одноименных горизонтальных проекций, т. е. c2║ d2║ x12и c3║ d3║ y3. Но горизонтальные их проекции не параллельны, т. е. c1╫ d1. Следовательно, прямые c и d не параллельны.
Пересекающиеся прямые. Две пересекающиеся прямые лежат в одной плоскости и имеют одну общую точку. Из свойств параллельных проекций известно, что если точка лежит на прямой, то ее проекции лежат на проекциях прямой. Если точка лежит и на той и на другой прямой, т. е. в точке пересечения прямых, то ее проекция должна лежать сразу на двух одноименных проекциях прямых, а следовательно, в точке пересечения проекций прямых.
Так, если отрезки AB и CD двух прямых пересекаются в точке K, то проекции отрезков A1B1 и C1D1 пересекаются в точке K1, являющейся проекцией точки K (рис. 2.26, а). Поэтому, если одноименные проекции прямых пересекаются в точках, лежащих на одной линии проекционной связи, то прямые в пространстве пересекаются (рис. 2.26, б).
Для определения того, пересекаются прямые или нет, достаточно, чтобы это условие выполнялось для двух каких-либо проекций. Исключение составляет случай, когда одна из пересекающихся прямых является профильной уровня. В этом случае для проверки пересечения прямых необходимо построение профильной проекции.
Пусть через точку A необходимо провести горизонталь b, пересекающую прямую a (рис. 2.27, а). Для этого через точку A2проводим b2║ x12 (этап 1) до пересечения с a2 в точке K2 (рис.2.27, б). Далее с помощью линии проекционной связи на a1 находим точку K1(этап 2) и, соединяя точки A1 и K1 (этап 3), получаем b1.
Скрещивающиеся прямые.Скрещивающиеся прямые a и b не лежат в одной плоскости и, следовательно, не параллельны и не имеют общих точек (рис.2.28, а). Поэтому, если прямые скрещивающиеся, то хотя бы одна пара их одноименных проекций не параллельна, и точки пересечения одноименных проекций не лежат на одной линии проекционной связи (рис. 2.28, б).
Каждая такая точка пересечения является проекцией двух точек, принадлежащих прямым; эти две точки лежат на одном проецирующем луче и называются конкурирующими.
Точки K и L (рис. 2.28, а) лежат на одном горизонтально-проецирующем луче. Горизонтальные проекции точек совпадают и находятся в точке пересечения горизонтальных проекций a1 и b1 прямых. Точка K a, точка L b. Видно, что точка K выше точки L. Считают, что при проецировании на П1 точка K видна, а точка L — не видна (закрыта от наблюдателя точкой К).
Точки M и N лежат на одном фронтально-проецирующем луче (рис. 2.28, б). Фронтальные проекции точек совпадают и находятся в точке пересечения фронтальных проекций прямых a2 и b2. Точка M a, точка N b. Точка N дальше от П2, чем точка M, т. е. ближе к глазам наблюдателя, и поэтому при проецировании на П2 точка N видна, а точка M — не видна. Обозначения проекций невидимых точек принято заключать в круглые скобки.
2.1. Задание прямой на эпюре
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.
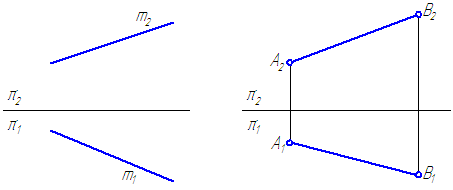
а б
Рисунок 2.1 – Проекции прямой
Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.
Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.
2.2. Прямые частного положения
Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.
Прямые, параллельные плоскостям проекций, называются прямыми уровня.
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).
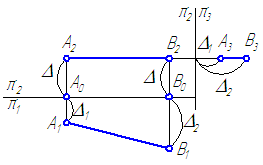
Рисунок 2.2 – Эпюр горизонтали
| Интерактивная модель Проекции горизонтали |
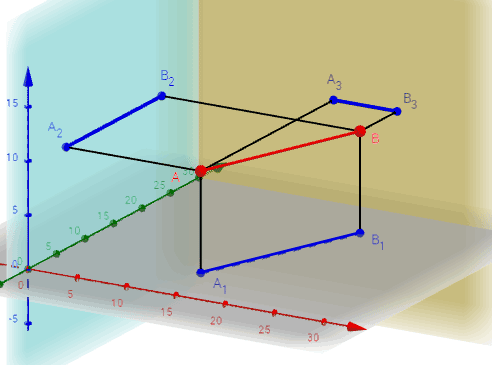 |
Если отрезок параллелен плоскости проекций π1, то его фронтальная проекция А2В2 параллельна оси проекций π1/π2, а горизонтальная проекция отрезка А1В1 определяет истинную величину АВ:
А2А0=В2В
А2В2 || π2/π1
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).
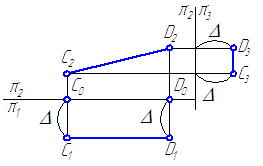
Рисунок 2.3 – Эпюр фронтали
| Интерактивная модель Проекции фронтали |
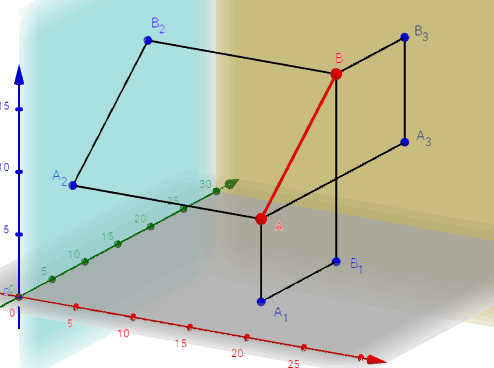 |
Если отрезок параллелен плоскости проекций π2, то его горизонтальная проекция параллельна оси проекций π2/π1, а фронтальная проекция отрезка C2D2 определяет истинную величину CD.
С1А0=D1D
C1D1 || π2/π1
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).
| Интерактивная модель Проекции профильной прямой |
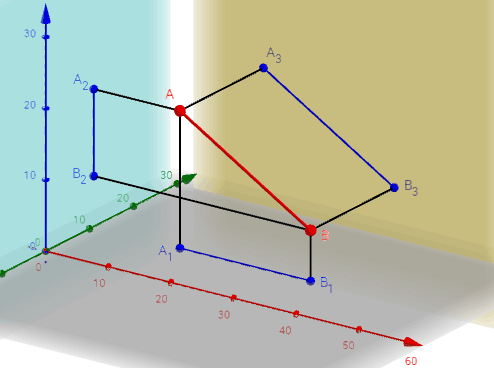 |
Прямые, перпендикулярные плоскостям проекций, называются проецирующими.
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).
Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).
Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).
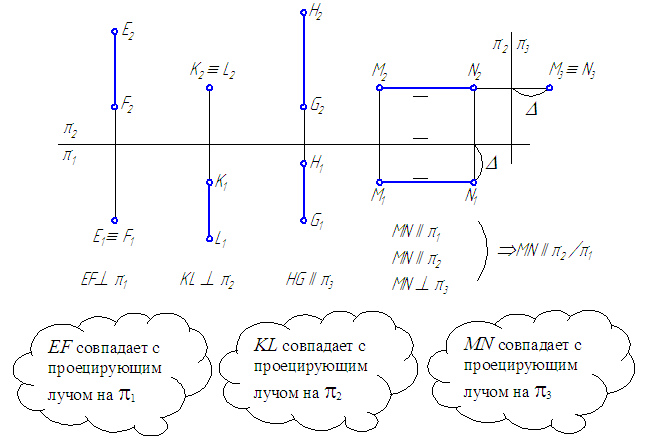
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH
2.3. Метод прямоугольного треугольника
Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π1 (Рисунок 2.5).
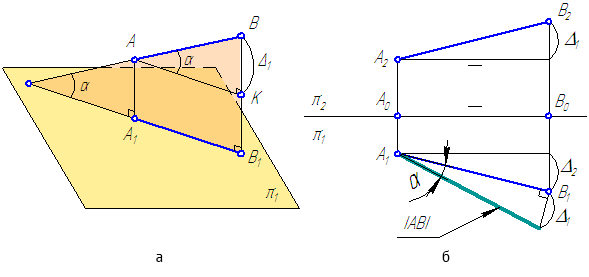
Рисунок 2.5 – Определение истинной величины отрезка общего положения
На рисунке 2.5, а:
АА1 – расстояние от точки А до плоскости проекций π1;
ВВ1 – расстояние от точки В до плоскости проекций π1;
А1В1 – проекция отрезка АВ на π1;
∠(AB; AK)=∠(AB; A1B1)=α – угол наклона прямой АВ к плоскости проекций π1.
ΔАКВ – прямоугольный треугольник, в котором:
АК=А1В1 – катет, равный горизонтальной проекции отрезка АВ;
ВК=ВВ1–АА1=Δ1 – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π1 (то есть, разности координат Z точек А и В);
АВ – гипотенуза ΔАКВ – истинная величина.
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.
Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А2В2), а другим – разность координат концов этого отрезка до плоскости (Δ2), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А2В2) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).
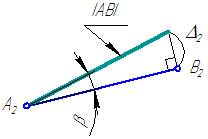
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
2.4. Точка и прямая
Если точка принадлежит прямой, то её проекции:
- Принадлежат одноимённым проекциям данной прямой;
- Лежат на одной линии связи.
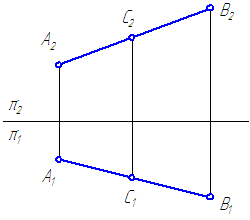
Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:
- С1∈А1В1;
- С2∈А2В2;
- С1С2⊥π2/π1;
Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:
{frac{A_2C_2}{C_2B_2}=frac{A_1C_1}{C_1B_1}=frac{AC}{CB}}
Справедливо и обратное утверждение.
Упражнение
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)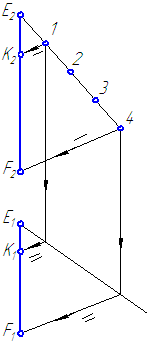
Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:
- Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е2.
- Отложим на этой прямой от точки Е2 равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
- Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F2.
- Из точки 1 проведём прямую, параллельную прямой (4—F2) до пересечения с проекцией E2F2, таким образом будет найдена фронтальная проекция искомой точки К2.
- Горизонтальную проекцию точки К1 получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.
Упражнение
Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).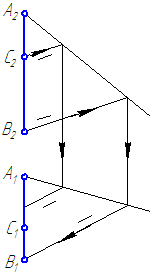
Рисунок 2.9а – Решение упражнения 2. Способ 1.
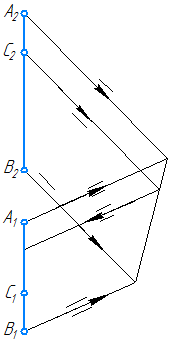
Рисунок 2.9б – Решение упражнения 2. Способ 2.
Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
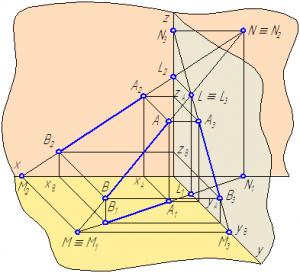
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
A1B1 ∩ xO =N1; YN=0; N ∈ xOz (π2) ⇒ AB ∩ xOz=N
A2B2 ∩ xO =M2; ZM=0; M ∈ xOy (π1) ⇒ AB ∩ xOy=M
A1B1 ∩ yO =L1; XL=0; L ∈ yOz (π3) ⇒ AB ∩ yOz=L
A2B2 ∩ zO =L2;
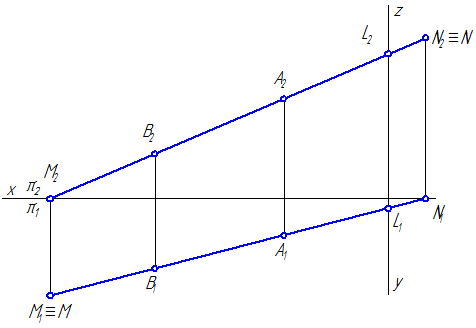
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ
| Интерактивная модель Проекции следов прямой |
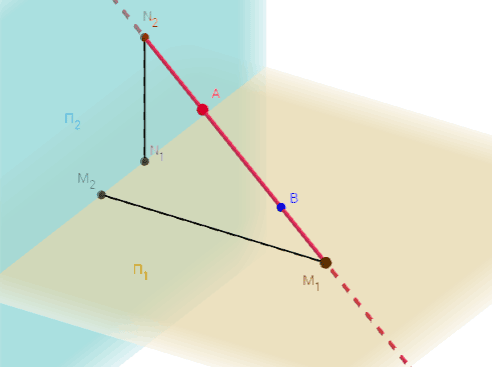 |
Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.
2.6. Взаимное расположение прямых
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).
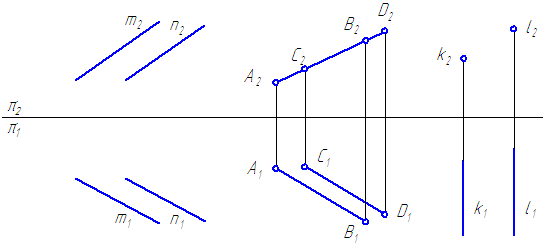
Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.
Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).
{{A_2B_2}cap{C_2D_2}=K_2}
{{A_1B_1}cap{C_1D_1}=K_1}
{frac{A_2K_2}{K_2B_2}=frac{A_1K_1}{K_1B_1}}
{frac{C_2K_2}{K_2D_2}=frac{C_1K_1}{K_1D_1}}
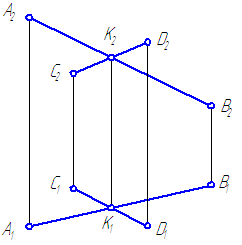
Рисунок 2.13 – Пересекающиеся прямые
Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).

Рисунок 2.14 — Скрещивающиеся прямые
2.7. Проекции плоских углов
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.
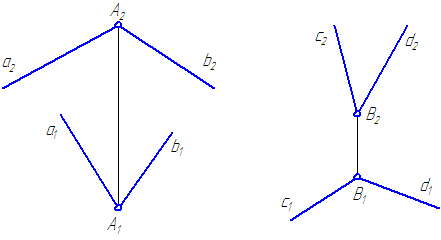
Рисунок 2.15
По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.
Теорема о проецировании прямого угла в частном случае
Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).
Обратная теорема. Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.
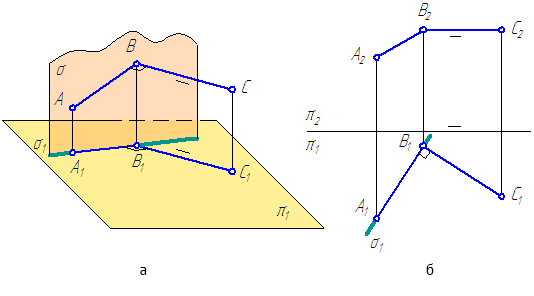
Рисунок 2.16 – Проецирование прямого угла
| Интерактивная модель Проецирование прямого угла |
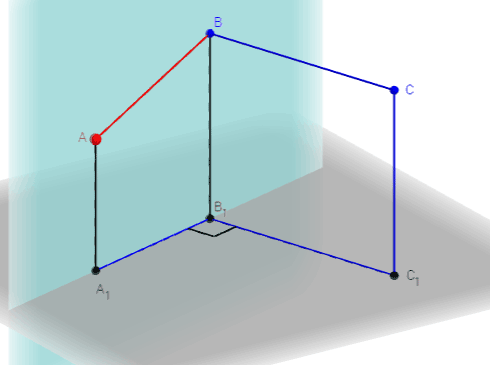 |
Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,
причём ВС // π1 (Рисунок 2.16,б).
Доказательство:
- Проведём через отрезок АВ проецирующую плоскость – σ, σ⊥π1;
- Прямые АВ и ВВ1 лежат в плоскости σ;
- ВС⊥ВВ1 так как ВС//π1, а ВВ1⊥π1;
- Следовательно, ВС⊥σ, а значит ВС перпендикулярна и любой прямой, лежащей в плоскости σ, в частности А1В1;
- Следовательно В1С1⊥σ;
- Так как В1С1//ВС, то В1С1⊥А1В1.
2.8. Задачи для самостоятельного решения
1. Построить отрезок прямой АВ // π1, равный 35 мм и наклонённый к π2 под углом 25° (Рисунок 2.17).
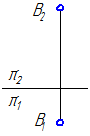
Рисунок 2.17
2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π2 и π1.
3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π1 и 45° — к плоскости проекций π2.
4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π2/π1 (Рисунок 2.18).
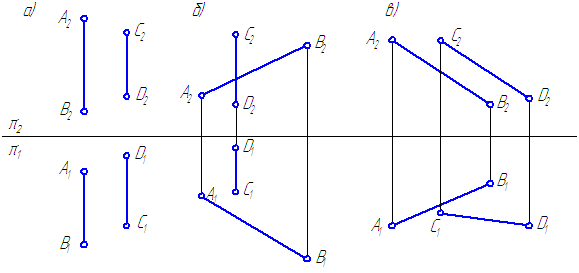
Рисунок 2.18
Ваша заявка отправленна
В скором времени мы с вами свяжемся
Лекция 2. ИЗОБРАЖЕНИЕ ПРЯМЫХ, ПЛОСКОСТЕЙ И МНОГОГРАННИКОВ
С О Д Е Р Ж А Н И Е
1. Прямые
1.1. Задание прямой.
1.2. Прямые общего положения
1.3. Прямые частного пложения
1.3.1. Прямые уровня
1.3.2. Проецирующие прямые
2. Плоскости
2.1. Задание плоскостей
2.2. Положение плоскостей
в системе координат
2.2.1.
Плоскости общего положения
2.2.2. Проецирующие плоскости
2.2.3. Плоскости уровня
3. Многогранники
4. Примеры построения многогранных поверхностей
4.1.
В перспективных проекциях системы Careldraw
4.2. Практические примеры получения сечений куба
плоскостями частного положения
Упражнение. Построить третью проекции 4-гранника
АВСД
1. Прямые
1.1. Задание прямой
Прямая линия определяется двумя точками, а ее проекции — проекциями этих
точек.
1.2. Прямые общего положения
Прямая не параллельная ни одной из плоскостей проекций, называется
прямой общего положения.
Прямая восходящая — ее признаком является одинаковое
направление проекций прямой относительно оси х, а нисходящей — разное
Прямая общего положения нисходящая — у нее одинаковое направление проекций
прямой относительно оси z, а у восходящей — разное
Рис. 1. Прямые общего положения: а) восходящая, б) нисходящая на наглядном
и комплексном чертежах
Рис.2 Прямая задана точками (следами) пересечения с координатными плоскостями
(рисунки получены в системе CG-Вектор)
1.3. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ
Прямые параллельные или перпендикулярные координатным плоскостям проекций
называются прямыми частного положения. Они делятся на: ПРЯМЫЕ УРОВНЯ- прямые
параллельные координатным плоскостям проекций и на ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
— это прямые перпендикулярные координатным плоскостям проекций.
1.3.1. ПРЯМЫЕ УРОВНЯ
ГОРИЗОНТАЛЬ (h // H)
ФРОНТАЛЬ (f // V)
ПРОФИЛЬНАЯ ПРЯМАЯ (P // W)
1.3.2. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Прямые перпендикулярные к какой-либо координатной плоскости называются
проецирующими прямыми.
Они делятся на горизонтально-проецирующие, фронтально-конкурирующие,
профильно-проецирующие. Проецирующие прямые имеют два важных свойства:
во первых они параллельны двум координатным плоскостям и значит на эти
плоскости они проецируются в натуральную величину; и второе — на плоскость
к которой они перпендикулярны они проецируются в точку (вырождаются в точку,
собирают все точки в одну точку), что упрощает решение многих задач встречающихся
в начертательной геометрии и, соответственно, в практике задач.
ГОРИЗОНТАЛЬНО — ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
ФРОНТАЛЬНО — ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
ПРОФИЛЬНО — ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
2. ПЛОСКОСТИ
2.1. Задание плоскостей
Плоскость определяется тремя точками, не лежащими на одной прямой. На ортогональном
чертеже плоскость может быть задана тремя точками, двумя пересекающими
прямыми, двумя параллельными прямыми, прямой и точкой, плоской фигурой
2.1.1. ПЛОСКОСТЬ ЗАДАНА ТРЕМЯ ТОЧКАМИ
2.1.2. ПЛОСКОСТЬ ЗАДАНА ДВУМЯ ПЕРЕСЕКАЮЩИМИСЯ ПРЯМЫМИ
2.1.3. ПЛОСКОСТЬ ЗАДАНА ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
2.1.3. ПЛОСКОСТЬ ЗАДАНА ПРЯМОЙ И ТОЧКОЙ
2.1.4. ПЛОСКОСТЬ ЗАДАНА ПЛОСКОЙ ФИГУРОЙ (ТРЕУГОЛЬНИКОМ)
2.1.5. ПЛОСКОСТЬ ЗАДАНА СЛЕДАМИ (ЛИНИЯМИ ПЕРЕСЕЧЕНИЯ ПЛОСКОЙ
ФИГУРОЙ С КООРДИНАТНЫМИ ПЛОСКОСТЯМИ)
Задание плоскости прямыми, по которым эта плоскость пересекает плоскости
проекций, называется заданием плоскости следами. Такое задание дает
прямую связь с аналитическим ее заданием (непосредственно алгоритмом для
ЭВМ), поэтому остановимся на этом более подробно.
Точки пересечения следов по осям x, y, z называются точками схода следов
плоскости. Расстояния от точек схода следов до начала координат называются
параметрами плоскости. Каждый след плоскости определяется двумя параметрами
и, следовательно, два следа плоскости определяют три ее параметра, т.е.
положение в пространстве.
Плоскость, заданная прямя параметрами (тремя числами), имеет аналог
аналитического задания. Так, например, плоскость Q (20,14,16) (рис. в)
определяется уравнением: x/a+y/b+z/c=1 или x/20+y/14+z/16=1, подобно
тому, как прямая задается на плоскости уравнением: x/a + y/b
= 1. В том и другом случае уравнения называются уравнениями (плоскости,
прямой) в отрезках. В частных случаях, когда прямая или плоскость параллельна
той или иной оси (а для плоскости и двум осям), слагаемые в уравнениях
с этой осью (осями) отсутствуют.
2.2. ПОЛОЖЕНИЯ ПЛОСКОСТЕЙ В СИСТЕМЕ КООРДИНАТ
Плоскость,
не перпендикулярная и не параллельная ни одной из плоскостей проекций,
называется плоскостью общего положения. Различают восходящие и нисходящие
плоскости общего положения. При обходе проекций вершин в одном и том направлении
у восходящей плоскости вершины располагаются на обеих проекциях одинаково,
а у нисходящей — различно. При этом восходящую плоскость иногда называют
односторонне видимой (на той и другой плоскости проекций видим одну сторону
плоскости), нисходящую плоскость — двусторонне видимой. Плоскость общего
положения, заданная следами, имеет три следа. Все следы наклонены к осям
проекций.
Плоскости, перпендикулярные плоскостям проекций, называется проецирующими.
Различают: горизонтально-проецирующие, фронтально-проецирующие, профильно-проецирующие.
Проекции всех точек проецирующей плоскости и всех линий плоских фигур,
лежащих в ней, принадлежат вырожденной проекции (следу) плоскости, к которой
она перпендикулярна. Это является важным свойством при решении многих задач
начертательной геометрии.
Плоскости, параллельные плоскостям проекций, называются плоскостями
уровня. Различают: Горизонтальная плоскость уровня ( G//H), фронтальная
плоскость уровня (F//V), профильная плоскость уровня (P//W).
Плоскости уровня одновременно перпендикулярны к двум плоскостям проекций,
обладают свойствами проецирующих плоскостей и своими, все плоские фигуры,
лежащие в ней проецируются на координатную плоскость к которой они параллельны
в натуральную (конгруэнтную) величину. Задавать (перезадавать) наиболее
удобно плоскость общего положения треугольником, а плоскости частного
положения — их вырожденными проекциями.
2.2.1. Плоскости
общего положения
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ ВОСХОДЯЩАЯ
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ НИСХОДЯЩАЯ
2.2.2. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ (заданы
вырожденными проекциями)
2.2.3. ПЛОСКОСТИ УРОВНЯ (заданы
вырожденными проекциями)
3. МНОГОГРАННИКИ
Многогранник
— пространственная фигура (трехмерное тело), ограниченное конечным числом
плоских многоугольников (многогранной поверхностью). Многоугольники называются
гранями, стороны многоугольников — ребрами, вершины — вершинами многогранников.
Существуют многогранники и как тела (в 4-хмерном пространстве они называются
гиперплоскостью), которые могут определены как твердые (твердотельная геометрия).
Нас пока интересуют только многогранники как поверхности.
Наиболее простыми многогранными поверхностями являются пирамида, куб,
призма и т.д. Построения таких фигур сводится к построению проекций точек
(вершин) и отрезков (ребер).
Важным является определение видимости ребер таких фигур, которая определяется
по следующему правилу: на фронтальной плоскости проекций видим то ребро
которое ближе к нам (это положение просматривается на горизонтальной проекции);
на горизонтальной проекции видим то ребро, которое выше (смотрим на предмет
сверху и это просматривается на фронтальной проекции). Для более строго
определения видимости, необходимо использовать алгоритм конкурирующих точек
(см. следующую тему).
4. Примеры построения многогранных поверхностей
4.1. В перспективных
проекциях системы Careldraw
4.2. ПРАКТИЧЕСКИЕ ПРИМЕРЫ ПОЛУЧЕНИЯ СЕЧЕНИЙ МНОГОГОГРАННИКА
(КУБА) ПЛОСКОСТЯМИ ЧАСТНОГО И ОБЩЕГО ПОЛОЖЕНИЙ
Горизонтально-проецирующие плоскости
Фронтально-проецирующие плоскости
Упражнение.
Построить третью проекции 4-гранника АВСД.
Как строить третью проекцию точки, есть два два способа:
| 1) при помощи координатных осей и линий связи, наглядно устанавливающих связь между всеми тремя проекциями фигуры; |
| 2) при помощи циркуля-измерителя (или линейкой), пользуясь которым можно строить третью проекцию, откладывая заданные размеры относительно ее осей. |
На рис. задача решена
первым способом: выбрана система координат (построены оси); третья проекция
построена по линиям связи.
Наглядный
чертеж построен в косоугольной изометрии, где фронтальная (вторичная) проекция
совпадает с фронтальной проекцией на ортогональном чертеже.
Построение осуществляется с помощью откладывания координат y каждой
точки по прямым параллельно оси y.
Видимость на ортогональном чертеже определяется по принципу:
на плоскости H видим то ребро(смотрим на V), которое выше; на V видим
то ребро которое ближе (смотрим на Н), на W видим то ребро которое левее
(смотрим на V).
В аксонометрии видим то, что ближе (объект с осями расположен перед
наблюдателем.

