Какие прямые называются перпендикулярными каким свойством они

Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.).
Для обозначения перпендикулярности имеется общепринятый символ:
, предложенный в 1634 году французским математиком Пьером Эригоном.
Например, перпендикулярность прямых и записывают как .
На плоскости[править | править код]
Перпендикулярные прямые на плоскости[править | править код]
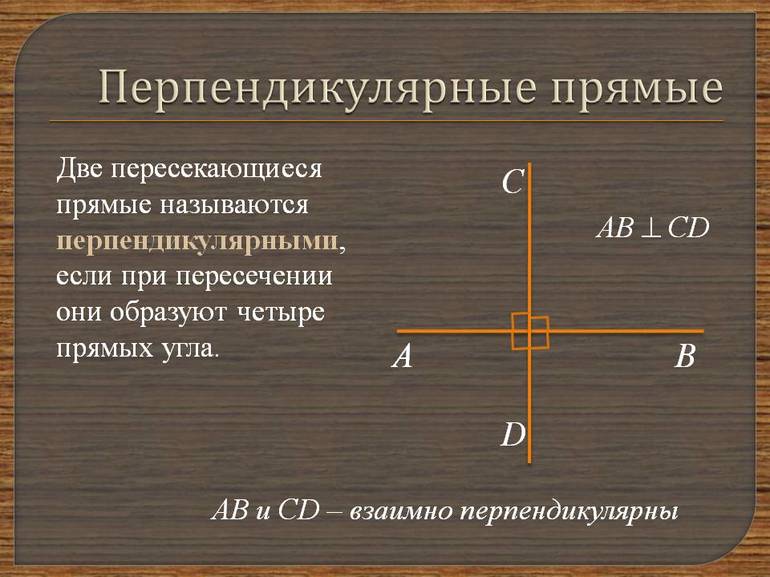
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую перпендикулярную к прямой проведённую через точку вне прямой , говорят, что есть перпендикуляр опущенный из на .
Если же точка лежит на прямой , то говорят, что есть перпендикуляр к восстановленный из к (устаревший термин восставленный[1]).
В координатах[править | править код]
В аналитическом выражении прямые, заданные линейными функциями
и
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
Построение перпендикуляра[править | править код]
Построение перпендикуляра
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.
Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой[править | править код]
Пусть прямая задаётся точками и . На прямую опускается перпендикуляр из точки .
Тогда основание перпендикуляра можно найти следующим образом.
Если (вертикаль), то и .
Если (горизонталь), то и .
Во всех остальных случаях:
;.
В трёхмерном пространстве[править | править код]
Перпендикулярные прямые[править | править код]
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямой к плоскости[править | править код]
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости[править | править код]
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения[2].
В многомерных пространствах[править | править код]
Перпендикулярность плоскостей в 4-мерном пространстве[править | править код]
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).
Перпендикулярность прямой и гиперплоскости[править | править код]
Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством и гиперплоскость с направляющим векторным пространством (где , ) принадлежат пространству .
Прямая l называется перпендикулярной гиперплоскости , если подпространство ортогонально подпространству , то есть
Вариации и обобщения[править | править код]
См. также[править | править код]
- Нормаль
- Параллельность
- Ортогональность
- Высота
- Теорема о трёх перпендикулярах
Примечания[править | править код]
Перпендикулярные прямые.
Вспомним взаимное расположение двух прямых. Две прямые могут пересекаться, т.е. иметь одну общую точку; могут не пересекаться, т.е. не иметь общих точек; и могут совпадать, т.е. иметь бесконечно много общих точек. Из этих трёх вариантов только пересечение двух прямых имеет разновидности. При пересечении двух прямых получается четыре угла, среди которых есть две пары вертикальных углов и четыре пары смежных углов. Но есть один случай, когда все четыре угла одинаковые. Это тот случай, когда каждый из четырёх углов – прямой, т.е. градусная мера каждого угла равна . Это особый случай пересекающихся прямых.
Определение. Перпендикулярными называются прямые, которые пересекаются под прямым углом (под углом ).

ТЕОРЕМА I: Через каждую точку прямой можно провести перпендикулярную ей прямую, и, притом, только одну.

Дано: – прямая, .
Доказать: .
Доказательство.
1. Так как , то она разделила прямую на две полупрямые: и . По аксиоме VII (от любой полупрямой, от её начальной точки, в заданную полуплоскость можно отложить угол заданной градусной меры, меньшей и, притом, только один) от полупрямой , от её начальной точки можно отложить угол , равный . Значит, прямая , проходящая через точку образует с прямой прямой угол, т.е. (по определению).
2. Докажем, что прямая единственная. Предположим, что существует ещё одна прямая , проходящая через точку , и составляющая с прямой прямой угол. Тогда . А это противоречит той же аксиоме VII, которая утверждает, что угол заданной градусной меры можно отложить только один. К противоречию пришли потому, что сделали неправильное предположение, значит, второй прямой , перпендикулярной прямой и проходящей через точку не существует.
3. Итак, , ч.т.д.
ТЕОРЕМА II: Через любую точку, не лежащую на данной прямой можно провести перпендикулярную ей прямую, и, притом, только одну.

Дано: – прямая, .
Доказать: .
Доказательство.
1. Выберем на прямой произвольную точку . Это возможно по аксиоме I (существуют точки принадлежащие и не принадлежащие прямой). Через две точки и можно провести прямую и только одну (аксиома I). Эта прямая будет пересекать прямую под некоторым углом. Так как прямая состоит из бесконечного количества точек, то существует бесконечное множество прямых, проходящих через точку и пересекающих прямую . И среди этого бесконечного множества прямых есть прямая, которая будет составлять с прямой прямой угол, т.е. .
2. Докажем, что прямая единственная. Предположим, что существует ещё одна прямая , проходящая через точку , и составляющая с прямой прямой угол. Тогда получается треугольник , в котором два угла прямые. Но как бы вы ни старались, вы не сможете построить треугольник с двумя прямыми углами. Его попросту не существует. Значит, мы сделали неправильное предположение, т.е. ещё одной прямой, проходящей через точку и перпендикулярной прямой не существует.
3. Итак, , ч.т.д.
Свойство. Углы с соответственно перпендикулярными сторонами либо равны, либо в сумме составляют .


Определение. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов точку их пересечения. Эта точка называется основанием перпендикуляра.

и – перпендикуляры к прямой .
Определение. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из этой точки на данную прямую.
Перпендикулярные прямые обладают ещё другими свойствами, но мы их рассмотрим позднее, после изучения параллельных прямых.
Построение прямых углов на местности.
Изучая построение углов на местности, мы познакомились с основными инструментами, которые используются для этой цели. Но все они использовались, в основном, для измерения углов. А для построения прямых углов существует простейший прибор – экер, а также более современный прибор – теодолит (или электронный тахеометр).
Экер – это простейший прибор, предназначенный для построения прямого угла. Он состоит из двух брусков, расположенных под углом , и закреплённых на треножнике. На краях брусков вбиты гвозди так, что прямые, которые проходят через них перпендикулярны друг другу. Отвес служит для точной установки экера в нужное место на местности.

Чтобы построить прямой угол с заданной стороной , треножник с экером устанавливают в том месте, где должна располагаться вершина прямого угла (точка ), при этом, экер должен быть в горизонтальной плоскости, а отвес, подвешенный в точке пересечения перпендикулярных прямых, проходящих через гвозди, должен находиться точно над вершиной угла . Затем необходимо установить один из брусков так, чтобы его направление совпадало с направлением заданной стороны (), совмещение этих направлений можно осуществить с помощью вехи, установленной в точке . Далее по направлению второго бруска провешивают прямую линию (). Получаем прямой угол на местности.
Теодолит – это измерительный прибор, предназначенный для построения и измерения горизонтальных и вертикальных углов при топографических съёмках, геодезических работах, в строительстве и т.п. Основной рабочей мерой в теодолите являются лимбы с градусными и минутными делениями.
Построение прямого, как, впрочем, и любого другого угла с помощью теодолита – достаточно сложный процесс. Нам достаточно знать о его существовании, и как он выглядит.
Используя данные, отмеченные на рисунках, укажите перпендикулярные прямые.


Начертите угол и отметьте три точки: одна из которых лежит во внутренней области угла; другая – во внешней области угла; третья – на стороне угла. Проведите через эти точки прямые, перпендикулярные обеим сторонам данного угла. Запишите необходимые обозначения.
Докажите, что если биссектрисы углов и перпендикулярны, то точки и лежат на одной прямой.
При пересечении прямых и образовались четыре угла. Луч перпендикулярен прямой и проходит между сторонами угла . Найдите угол , если . Сделайте рисунок.
Через вершину угла , равного , проведена прямая так, что . Найдите угол между прямой и прямой, содержащей биссектрису данного угла.

На рисунке изображён куб. Запишите прямые, перпендикулярные прямой и прямые, перпендикулярные прямой , на которых лежат рёбра куба.

Равны ли острые углы и , если ? Ответ обоснуйте.
Чему равна сумма острого угла и тупого угла , если ? Ответ обоснуйте.
На рисунке прямые и перпендикулярны, . Найдите .

На рисунке прямые и перпендикулярны, . Найдите .

На рисунке из точки проведены лучи и , причём, . Угол, образованный биссектрисами углов и , равен . Найдите углы и .

На рисунке из точки проведены лучи и , причём, . Угол, образованный биссектрисами углов и , равен . Найдите углы и .

На рисунке даны два угла и с общей вершиной. Стороны одного угла перпендикулярны к сторонам другого угла. Найдите эти углы, если разность между ними равна прямому углу.
Углы и смежные, – биссектриса угла , луч принадлежит области угла и перпендикулярен . Является ли биссектрисой угла ? Ответ обоснуйте.

Два равных тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны. Найдите величину тупого угла.
Из вершины развёрнутого угла проведены два луча, которые делят его на три равные части. Докажите, что биссектриса среднего угла перпендикулярна сторонам развёрнутого угла.
Докажите, что сумма каждых трёх углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна двум прямым углам.
Докажите, что сумма каждых пяти углов, не прилежащих один к другому и образуемых пятью прямыми, проходящими через одну точку, равна двум прямым углам.
Докажите, что биссектрисы смежных углов перпендикулярны.
Докажите, что две прямые, перпендикулярные одной прямой, не имеют общих точек.
Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
Даны три прямые . Докажите, что если и , то прямые и не имеют общих точек.
Докажите, что если три из четырёх углов, которые получаются при пересечении двух прямых, равны, то прямые перпендикулярны.
С помощью угольника проведите прямые, перпендикулярные прямым, изображённым на рисунке.

На рисунке пересекаются три прямые. Запишите, какие из этих прямых перпендикулярны. Найдите остальные углы.

На рисунке прямые и перпендикулярны, . Найдите .

На рисунке прямые и перпендикулярны, . Найдите .

Даны два непересекающихся угла с общей вершиной, причём, их стороны соответственно перпендикулярны, и один угол в два раза меньше другого. Найдите эти углы.
Даны два пересекающихся по лучу угла и , причём, известно, что их сумма составляет прямого угла, и что продолжение стороны за вершину делит угол пополам. Найдите эти углы.
Через вершину угла, равного , проведена прямая, перпендикулярная его биссектрисе. Чему равны углы, образованные этой прямой и сторонами данного угла?
7

Основные свойства
При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:
- Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.
- Несколько перпендикуляров никогда не будут между собой пересекаться.
Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.
Доказательство взаимного расположения
Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:
- Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
- Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.
Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.
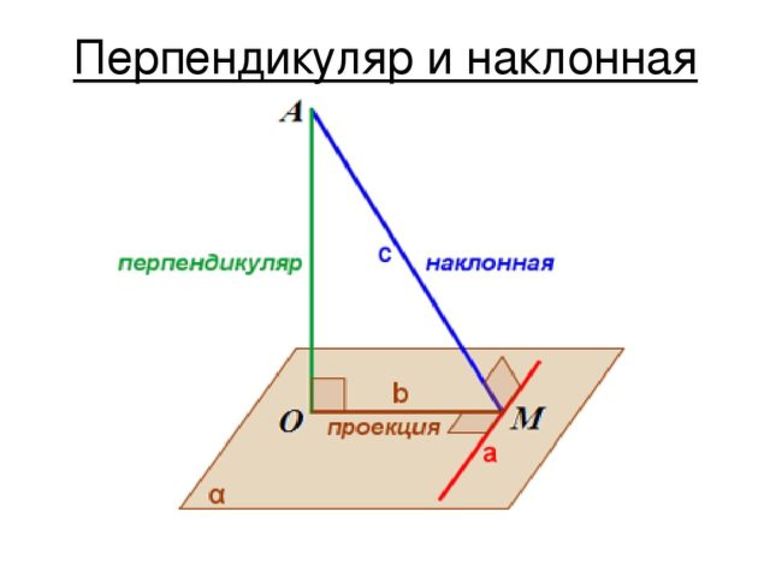
Определение перпендикулярности прямой и плоскости
Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.
Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:
- Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
- В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.
Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.
Построение перпендикуляра
Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:
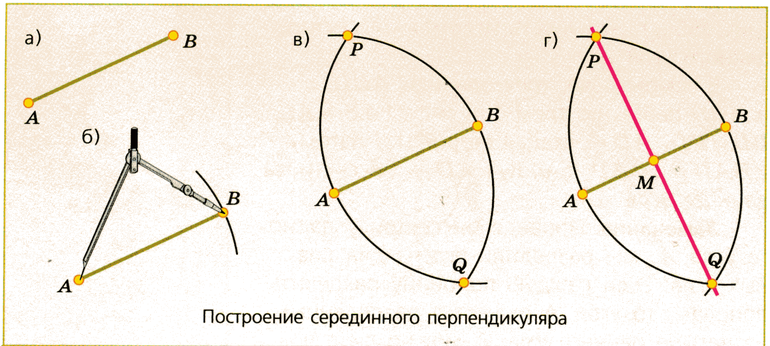
- С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
- С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.
Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:
- Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
- Проводится откладывание вертикального отрезка.
В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.
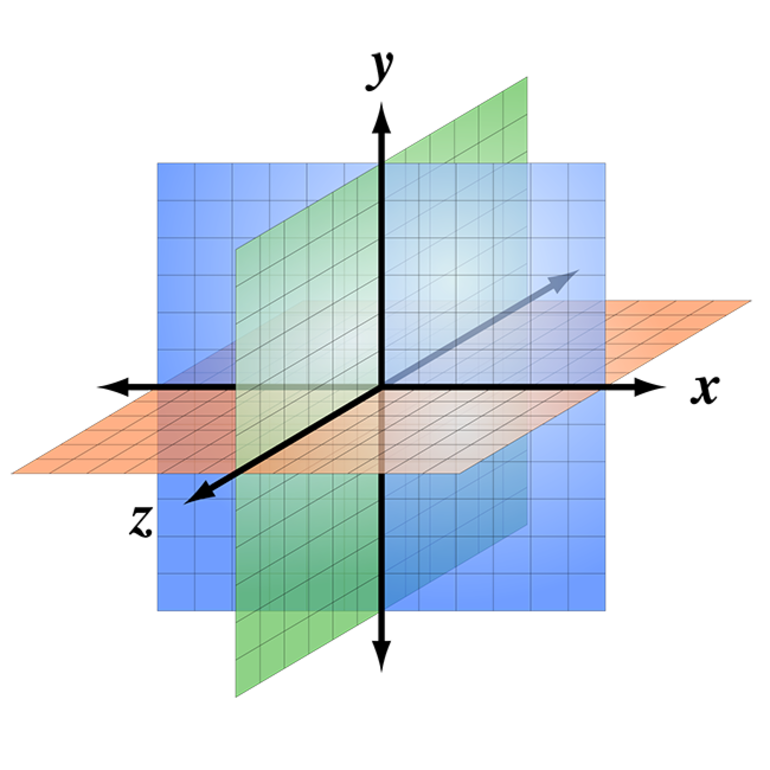
Трехмерное пространство
В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:
- Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.
- Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.
- Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.
В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.
Четырехмерная система координат и лемма
Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.
Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:
- Они должны пересекаться в точке.
- Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.
Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.
Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:
- Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
- Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
- Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.
При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.
Применение термина
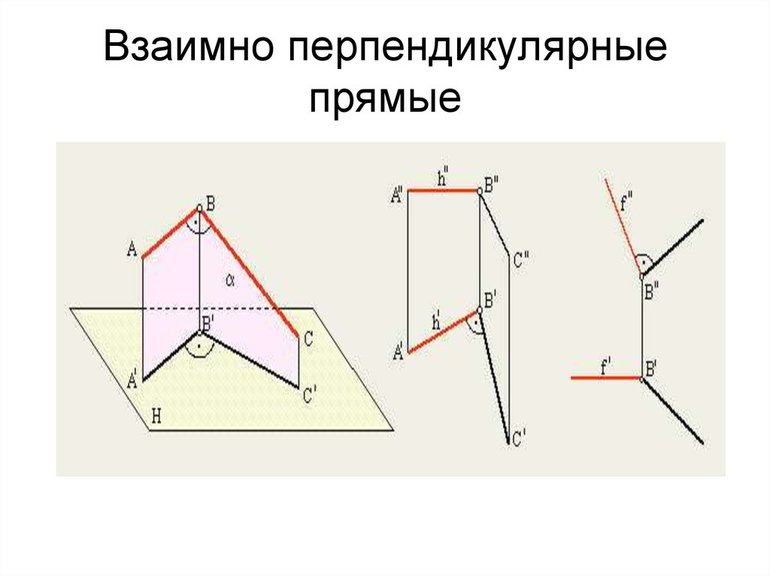
Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.
В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.
В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.
Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.
Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.
