Какие основные свойства площадей многоугольников
[{Large{text{Основные факты о площади}}}]
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см(^2), мм(^2) соответственно.
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4. Площадь квадрата со стороной (a) равна (a^2).
[{Large{text{Площадь прямоугольника и параллелограмма}}}]
Теорема: площадь прямоугольника
Площадь прямоугольника со сторонами (a) и (b) равна (S=ab).
Доказательство
Достроим прямоугольник (ABCD) до квадрата со стороной (a+b), как показано на рисунке:

Данный квадрат состоит из прямоугольника (ABCD), еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b). Таким образом,
(begin{multline*} S_{a+b}=2S_{text{пр-к}}+S_a+S_b Leftrightarrow
(a+b)^2=2S_{text{пр-к}}+a^2+b^2 Leftrightarrow\
a^2+2ab+b^2=2S_{text{пр-к}}+a^2+b^2 Rightarrow
S_{text{пр-к}}=ab end{multline*})
Определение
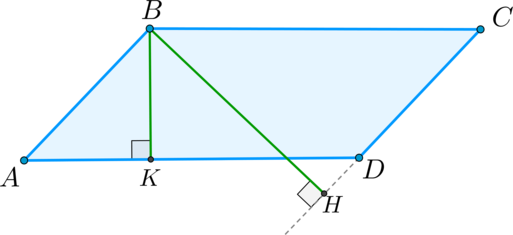
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD), а высота (BH) — на продолжение стороны (CD):
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры (AB’) и (DC’), как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD).

Тогда (AB’C’D) – прямоугольник, следовательно, (S_{AB’C’D}=AB’cdot
AD).
Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,
(S_{ABCD}=S_{ABC’D}+S_{DCC’}=S_{ABC’D}+S_{ABB’}=S_{AB’C’D}=AB’cdot
AD.)

[{Large{text{Площадь треугольника}}}]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть (S) – площадь треугольника (ABC). Примем сторону (AB) за основание треугольника и проведём высоту (CH). Докажем, что [S = dfrac{1}{2}ABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:
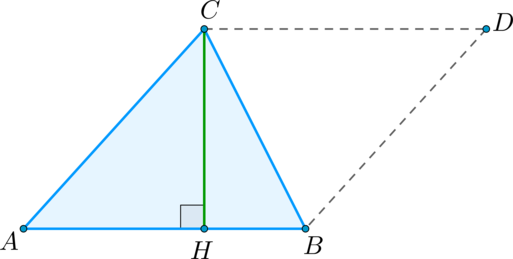
Треугольники (ABC) и (DCB) равны по трем сторонам ((BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC)), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC), то есть (S = dfrac{1}{2}ABcdot CH).
Теорема
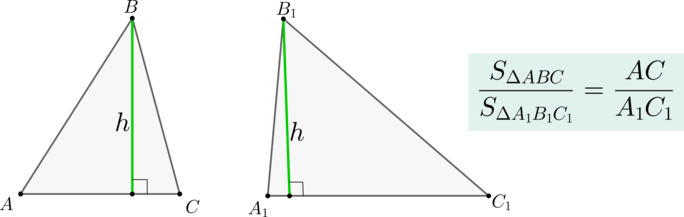
Если два треугольника (triangle ABC) и (triangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
Если два треугольника (triangle ABC) и (triangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
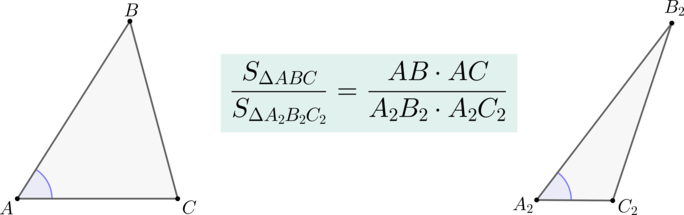
Доказательство
Пусть (angle A=angle A_2). Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2)):
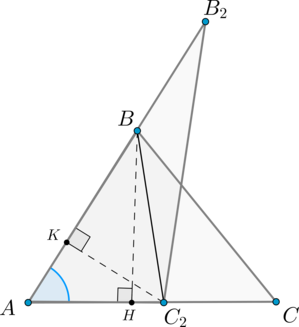
Проведем высоты (BH) и (C_2K).
Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K), следовательно: [dfrac{S_{AB_2C_2}}{S_{ABC_2}}=dfrac{AB_2}{AB}]
Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH), следовательно: [dfrac{S_{ABC_2}}{S_{ABC}}=dfrac{AC_2}{AC}]
Перемножая последние два равенства, получим: [dfrac{S_{AB_2C_2}}{S_{ABC}}=dfrac{AB_2cdot AC_2}{ABcdot AC} qquad text{ или
} qquad dfrac{S_{A_2B_2C_2}}{S_{ABC}}=dfrac{A_2B_2cdot
A_2C_2}{ABcdot AC}]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть (p) – полупериметр треугольника, (a), (b), (c) – длины его сторон, тогда его площадь равна [S_{triangle}=sqrt{p(p — a)(p —
b)(p — c)}]

[{Large{text{Площадь ромба и трапеции}}}]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник (ABCD). Обозначим (AO=a, CO=b, BO=x,
DO=y):
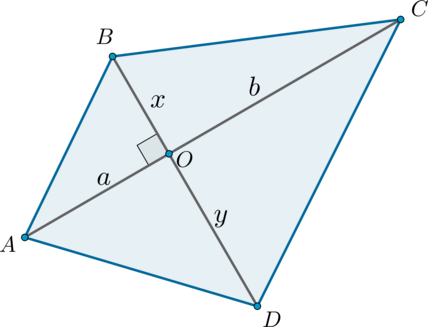
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
(begin{multline*}
S_{ABCD}=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\
frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end{multline*})
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: [S_{text{ромб}}=dfrac12 d_1cdot d_2]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
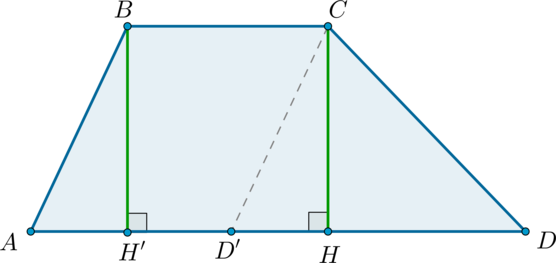
Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD). Проведем (CD’parallel AB), как показано на рисунке:

Тогда (ABCD’) – параллелограмм.
Проведем также (BH’perp AD, CHperp AD) ((BH’=CH) – высоты трапеции).
Тогда (S_{ABCD’}=BH’cdot AD’=BH’cdot BC, quad S_{CDD’}=dfrac12CHcdot D’D)
Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’cdot BC+dfrac12CHcdot
D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12
CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
a1 = a2 = a3 = … = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn
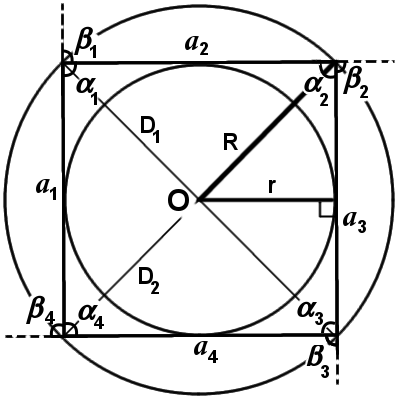
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
2. Формула площади n-угольника через радиус вписанной окружности:
3. Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
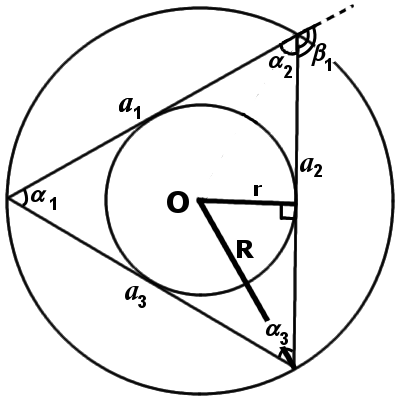 |
| Рис.3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
α = 135°
Тема урока: «Площадь многоугольника» (8 класс).
Геометрия, развивая ум, обогащает
всякого трудящегося в ней элементом
общечеловеческой культуры –
геометрическими знаниями
Е.Е. Семенов
Цели урока:
Образовательные:
Дать представление об измерении площадей многоугольников.
Рассмотреть основные свойства площадей.
Показать примеры использования изученного теоретического материала в ходе решения задач.
Развивающие: развить умение вычислять площади фигур, применяя изученные свойства, развитие логического мышления и математической культуры.
Воспитательные: воспитание познавательного интереса к геометрии.
Тип урока: урок объяснения нового материала.
Метод: комбинированный ( словесно-наглядно-практический — проблемный).
Структура урока
Организационно-психологический момент.
Мотивация учебной деятельности учащихся, постановка целей урока.
Актуализация знаний:
1) Подготовка к восприятию нового материала.
2) Объяснение нового материала.
а) Ввести понятие площади.
б) Единицы измерения площадей и измерение площади многоугольника способом разбиения фигуры на квадраты.
в) Свойства площадей.
г) Понятие равновеликости и равносоставленности.
Закрепление изученного материала.
Итоги урока.
Домашнее задание.
Ход урока
I. Организационно-психологический момент.
II. Мотивация учебной деятельности учащихся, постановка целей урока.
III. Актуализация знаний.
Устное решение задачи
Через точку во внутренней области равностороннего треугольника проведены 2 прямые, параллельные двум сторонам треугольника. На какие фигуры разбивается этими прямыми данный треугольник?
Показать их на рисунке.
Подготовка к восприятию нового материала.
Диалог
Таня: — Мне нужна площадь города Витебска!
Настя: — Ну что вы! В Витебске много площадей: Победы, Свободы, Ленина,… Вам какую нужно?
Таня: — Мне нужна площадь в квадратных километрах!
Настя: — Знаете, о такой площади я что-то не слыхала. Может, Вы ошиблись городом?
Учитель: — Ребята, не догадались ли вы какова тема нашего сегодняшнего урока?
Объяснение нового материала.
Вводная беседа.
В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты 12 м2, площадь садового участка 3 ара. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку и вычисление площадей участков, покрытых плодоносным илом. Впоследствии было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника и других многоугольников. С сегодняшнего дня мы будем вычислять площади различных фигур.
Как и измерение длин отрезков, измерение площадей проводится с помощью единиц измерения. За единицу измерения площадей принимается квадрат со стороной, равной единице измерения отрезков. Площадь такого квадрата считается равной 1.
1см 2, 1 дм 2, 1 м 2.
Как вы понимаете утверждение «единица измерения площади 1 квадратный сантиметр»?
(Площадь измеряется квадратами со стороной 1см, или единичный квадрат- квадрат, сторона которого служит единицей длины)
Может ли площадь фигуры выражаться отрицательным числом? (Нет).
Площадь многоугольника выражается положительным числом, которое показывает сколько раз единица измерения и ее части укладываются в многоугольнике.
Итак, площадь — это некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или на иной поверхности. Мы пока будем рассматривать лишь плоские фигуры, поэтому площадь — это положительное число, которое ставится в соответствие ограниченной плоской фигуре. Обычно площадь обозначается буквой S.
При выбранной единице измерения площадей площадь каждого многоугольника показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.
Как измерить площадь фигуры? Сначала нужно выбрать единицу площади, т.е. указать единичный квадрат, т.е. квадрат, сторона которого служит единицей длины.

Практически это можно сделать так: расчерчиваем лист на квадраты, со стороной, равной единице измерения отрезков и накладываем на него фигуру. Пусть m – число квадратов полностью покрытых многоугольником. Их общая площадь S1, n – число квадратов частично покрытых фигурой, их площадь S2, тогда S1Sфиг. S2. Практически за площадь фигуры можно взять величину (но эта формула дает большую погрешность). Для более точных результатов разбиваем каждый из частично покрытых многоугольников на более мелкие квадраты. Тем самым приближая числа к площади фигуры. Чем более мелкая единица измерения, тем более точное вычисление площади. Однако этот способ на практике неудобен. Обычно измеряют лишь некоторые отрезки многоугольника, а затем вычисляют его площадь по определенным формулам. Их вывод основан на свойствах площадей, которые сейчас будут доказаны.
Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Площадь квадрата равна квадрату его стороны.
С понятием площадей неразрывно связаны равносоставленность и равновеликость.
Если один многоугольник разрезать на части и составить из них другой многоугольник, то такие многоугольники называются равносоставленными.
Примером равносоставленных фигур может служить китайская головоломка «Танграм», которую в Китае называют «чи тао ту», т.е. умственная головоломка из семи частей.
Два многоугольника называются равновеликими, если их площади равны.
Примером таких многоугольников согласно свойству 1 могут служить любые равные многоугольники.
Обратное утверждение неверно. Равновеликие многоугольники могут быть неравными (прямоугольник и треугольник с площадями 15 см2).
В силу 2 свойства площадей равносоставленные многоугольники равновелики.
Обратное утверждение также верно.
Любые два равновеликих многоугольника равносоставлены. Это утверждение называется теоремой Бойяви – Гервина. (Бойяви — венгерский математик, доказал теорему в 1832 г., Гервин – немецкий математик-любитель, доказал теорему независимо от Бойяви в 1833 году).
Следствие из теоремы Бойяви – Гервина: любой многоугольник можно разрезать на такие части, из которых можно составить равновеликий этому многоугольнику квадрат.
IV. Закрепление изученного.
Решить задачу № 448
V. Итоги урока. Выставление оценок ученикам, активно работавшим на уроке.
Домашнее задание: п.48 ( выучить свойства площадей)
№446, №447
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
1. Основные свойства площадей многоугольников.
2 . Сформулировать и доказать теорему о вычислении площади трапеции.
3. Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
4. Расскажите, как измеряются площади многоугольников.
5. Сформулируйте и докажите теорему о вычислении площади треугольника.
6. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте теорему о площадях двух треугольников , имеющих по равному углу.
8. Сформулируйте и докажите теорему ПИФАГОРА.
9. Сформулируйте и докажите теорему, обратную теореме Пифагора.
10. Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
