Какие есть свойства прямоугольника

Прямоугольник, свойства, признаки и формулы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение)
Свойства прямоугольника
Признаки прямоугольника
Формулы прямоугольника
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
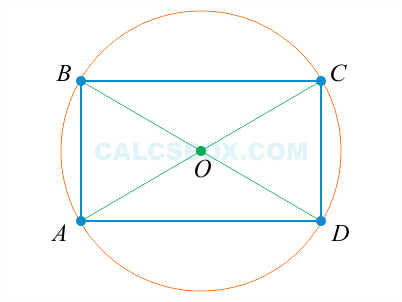
6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Рис. 11. Квадрат
AВ = ВC = AD = CD
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Формула диагонали прямоугольника:
![]() ,
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:
 .
.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
1 397
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это…
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
Судите сами:
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У прямоугольника равны противоположные стороны.
- У прямоугольника противоположные стороны параллельны.
- У прямоугольников все прилегающие друг к другу стороны пересекаются под прямыми углами. А в сумме они дают 360 градусов.
- У прямоугольников обе диагонали равны между собой.
- Диагональ прямоугольника делит фигуру ровно пополам, и в результате получаются два одинаковых прямоугольных треугольника.
- Диагонали прямоугольника пересекаются в его геометрическом центре. А их точка пересечения делит каждую диагональ на два равных отрезка. Более того, все четыре отрезка равны между собой.
- У прямоугольника точка пересечения диагоналей является еще и центром описанной вокруг окружности. Причем длина диагонали одновременна является диаметром (что это такое?) этой окружности.
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Подборки по теме
- Вопросы и ответы
- Использую для заработка
- Полезные онлайн-сервисы
- Описание полезных программ
Использую для заработка
- ВоркЗилла — удаленная работа для всех
- Анкетка — платят за прохождение тестов
- Etxt — платят за написание текстов
- Кьюкоммент — биржа комментариев
- Поиск лучшего курса обмена
- 60сек — выгодный обмен криптовалют
- Толока — заработок для всех в Яндексе
- Бинанс — надёжная биржа криптовалют
- ВкТаргет — заработок в соцсетях (ВК, ОК, FB и др.)
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ), ( angle B = angle D ))
2. Противоположные стороны равны
( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны
( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу
( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны
( AC = BD )

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ).
Следовательно, ( triangle ABD = triangle DCA ) по двум катетам (( AB = CD ) и ( AD ) — совместный).
Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.
Значит, ( AC = BD ).
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
( Rightarrow AB = CD ), ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.
Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ), ( angle B = angle D ).
Выводим, что ( angle A = angle B = angle C = angle D ). Все они по ( 90^{circ} ). В сумме — ( 360^{circ} ).
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
( AC^2=AD^2+CD^2 )
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

8. Точка пересечения диагоналей делит их пополам
( AO = BO = CO = DO )

9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности
10. Сумма всех углов равна 360 градусов
( angle ABC + angle BCD + angle CDA + angle DAB = 360^{circ} )
11. Все углы прямоугольника прямые
( angle ABC = angle BCD = angle CDA = angle DAB = 90^{circ} )

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна ( 180^{circ} )
( angle ABC = angle CDA = 180^{circ},enspace angle BCD = angle DAB = 180^{circ} )
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Прямоугольник уникален своей простотой. На основе этой фигуры ученики начинают познавать основы геометрии. Поэтому в старших классах теряются, не зная основных свойств и признаков прямоугольника, напрасно считая эту фигуру излишне простой.

Прямоугольник
Определение прямоугольника известно с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что же такое параллелограмм?
Несмотря на заковыристое название, эта фигура столь же проста, как и прямоугольник. Параллелограмм это выпуклый четырехугольник, стороны которого попарно равны и параллельны.
В определении обязательно выделять слово выпуклый. Поскольку выпуклые и невыпуклые четырехугольники четко разделяются в геометрии. Причем невыпуклые фигуры вообще не изучаются в школьном курсе математики, так как они куда более непредсказуемы в своих свойствах.

Рис. 1. Выпуклые четырехугольники
Прямоугольник это частный случай параллелограмма. При этом существуют как другие частные случаи параллелограмма, например, ромб; так и другие частные случаи прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.
Свойства прямоугольника
Свойства прямоугольника можно разбить на две группу: свойства параллелограмма и свойства прямоугольника.
Свойства параллелограмма:
- Противоположные стороны попарно равны и параллельны.
- Противоположные углы равны.
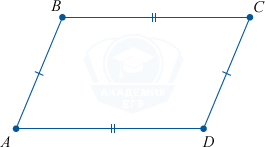
Рис. 2. Свойства параллелограмма
Свойства прямоугольника:
- Все углы равны 90 градусам, что проистекает из определения фигуры.
- Диагонали прямоугольника разбивает фигуру на два малых равных прямоугольных треугольника. Это свойство легко доказать. Треугольники будут прямоугольными, так как включат в себя по одному углу в 90 градусов. При этом диагональ будет являться общей стороной ,а катеты окажутся равными, так как противоположные стороны прямоугольника попарно равны и параллельны.
- Диагонали прямоугольника равны.
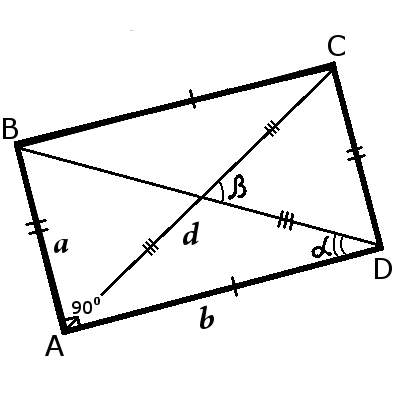
Рис. 3. Луч
Признаки прямоугольника
У прямоугольника всего три основных признака:
- По углу. Если один из углов параллелограмма равен 90 градусам, то параллелограмм является прямоугольником.
- Если три угла четырехугольника равны 90 градусам, то такой четырехугольник является прямоугольником. Обратите внимание, что в этом случае нет необходимости доказывать, что перед нами параллелограмм. Достаточно знать значения углов четырехугольника.
- По диагонали: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.
Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве.
В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.
Что мы узнали?
Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника. Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма.
Тест по теме
Оценка статьи
Средняя оценка: 4.1. Всего получено оценок: 366.
Ïðÿìîóãîëüíèê — ïàðàëëåëîãðàìì ñ ïðÿìûìè óãëàìè, ðàâíûìè 90 ãðàäóñàì è äâóìÿ ïðîòèâîïîëîæíûìè ðàâíûìè ñòîðîíàìè.

 åâêëèäîâîé ãåîìåòðèè äëÿ òîãî, ÷òîáû ÷åòûðåõóãîëüíèê îêàçàëñÿ ïðÿìîóãîëüíèêîì, íóæíî, ÷òîáû õîòÿ áû 3 óãëà áûëè ïðÿìûìè. ×åòâåðòûé óãîë òàêæå áóäåò ðàâåí 90°, èñõîäÿ èç òåîðåìû î ñóììå óãëîâ ìíîãîóãîëüíèêîâ.  íååâêëèäîâîé ãåîìåòðèè, åñëè ñóììà óãëîâ ÷åòûð¸õóãîëüíèêà áîëüøå èëè ìåíüøå 360 ãðàäóñîâ, òàêîé ÷åòûðåõóãîëüíèê íå ìîæåò áûòü ïðÿìîóãîëüíèêîì.
Ðàçíèöà â ïðÿìîóãîëüíèêàõ ëèøü â îòíîøåíèè äëèííîé ñòîðîíû ê êîðîòêîé, â òî âðåìÿ êàê êàæäûé èç ÷åòûðåõ óãëîâ ïðÿìîé (ðàâåí 90°).

Ñâîéñòâà ïðÿìîóãîëüíèêà.
Êðîìå ïàðàëëåëîãðàììà ïðÿìîóãîëüíèêîì ìîãóò áûòü åùå êâàäðàò è ðîìá.
— Ïðÿìîóãîëüíèê — ýòî ïàðàëëåëîãðàìì. Ïðîòèâîëåæàùèå ñòîðîíû ïàðàëëåëüíû äðóã äðóãó.
— Ñòîðîíû ïðÿìîóãîëüíèêà – ýòî åãî æå âûñîòû.
— Êâàäðàò äèàãîíàëè ïðÿìîóãîëüíèêà = ñóììå êâàäðàòîâ 2-õ ñìåæíûõ ñòîðîí (èç òåîðåìû Ïèôàãîðà).
— Âîêðóã âñÿêîãî ïðÿìîóãîëüíèêà ëåãêî îïèñàòü îêðóæíîñòü, ïðè ýòîì äèàãîíàëü ïðÿìîóãîëüíèêà áóäåò ðàâíîé ñ äèàìåòðîì îêðóæíîñòè, êîòîðàÿ îïèñàíà (òîãäà ðàäèóñ îêðóæíîñòè áóäåò ðàâåí ïîëóäèàãîíàëè ïðÿìîóãîëüíèêà).

— Ó ïðîòèâîïîëîæíûõ ñòîðîí ïðÿìîóãîëüíèêà îäèíàêîâàÿ äëèíà, ò.å. ñòîðîíû ðàâíû:
AB = CD, BC = AD
— Ïðîòèâîëåæàùèå ñòîðîíû ïðÿìîóãîëüíèêà ïàðàëëåëüíû äðóã äðóãó:
AB||CD, BC||AD
— Ïðèëåãàþùèå ñòîðîíû ïðÿìîóãîëüíèêà ïåðïåíäèêóëÿðíû:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
— Êàæäûé èõ ÷åòûðåõ óãëîâ ïðÿìîóãîëüíèêà ïðÿìîé:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
— Ñóììà óãëîâ ïðÿìîóãîëüíèêà ñîñòàâëÿåò 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
— Äèàãîíàëè ïðÿìîóãîëüíèêà èìåþò îäèíàêîâûå äëèíû:
AC = BD
— Ñóììà êâàäðàòîâ äèàãîíàëè ïðÿìîóãîëüíèêà ðàâíà ñóììå êâàäðàòîâ ñòîðîí:
2d2 = 2a2 + 2b2
— Âñå äèàãîíàëè ïðÿìîóãîëüíèêà äåëÿò ïðÿìîóãîëüíèê íà 2 îäèíàêîâûå ôèãóðû (åñëè êîíêðåòíåå, íà ïðÿìîóãîëüíûå òðåóãîëüíèêè).
— Äèàãîíàëè ïðÿìîóãîëüíèêà ïåðåñåêàþòñÿ, äåëÿ äðóã äðóãà íà 2 ðàâíûå ÷àñòè:
AO = BO = CO = DO = d/2
— Òî÷êó ïåðåñå÷åíèÿ äèàãîíàëåé íàçûâàþò öåíòðîì ïðÿìîóãîëüíèêà, êðîìå òîãî îíà åñòü öåíòð îïèñàííîé îêðóæíîñòè.
— Äèàãîíàëü ïðÿìîóãîëüíèêà åñòü äèàìåòð îêðóæíîñòè îïèñàííîé.
— Îêîëî ïðÿìîóãîëüíèêà ëåãêî îïèñàòü îêðóæíîñòü, ò.ê. ñóììà ïðîòèâîëåæàùèõ óãëîâ ðàâíà 180°:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
—  ïðÿìîóãîëüíèê ñ íåðàâíîé äëèíîé è øèðèíîé, íèêàê íå âïèñàòü îêðóæíîñòü, ò.ê. ñóììà ïðîòèâîïîëîæíûõ ñòîðîí íå ðàâíà ìåæäó ñîáîé (âïèñàòü îêðóæíîñòü ïîëó÷èòñÿ ëèøü â ÷àñòíûé ñëó÷àé ïðÿìîóãîëüíèêà — êâàäðàò).
Ïëîùàäü ïðÿìîóãîëüíèêà, îíëàéí ðàñ÷åò | |
| Ðàñ÷åò ïëîùàäè ïðÿìîóãîëüíèêà ïî øèðèíå è âûñîòå, äèàãîíàëÿì è óãëó ìåæäó íèìè, êàê íàéòè ïëîùàäü ïðÿìîóãîëüíèêà. | |
| Ïëîùàäü ïðÿìîóãîëüíèêà, îíëàéí ðàñ÷åò | |
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû — ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïàðàëëåëîãðàìì. | |
| Ïàðàëëåëîãðàìì — ýòî ÷åòûðåõóãîëüíèê ñ ïîïàðíî ïàðàëëåëüíûìè ïðîòèâîïîëîæíûìè ñòîðîíàìè (íàõîäÿòñÿ íà ïàðàëëåëüíûõ ïðÿìûõ). | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïàðàëëåëîãðàìì. | |
