Какие бывают треугольники и их свойства
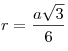
Понятие треугольника
Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.
Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Определение 1
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Определение 2
Точки в рамках определения 1 называются вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 называются сторонами треугольника.
Треугольник будем обозначать тремя точками его вершин (рис. 1)
Виды треугольников
Треугольники можно разделять на различные виды по углам и по сторонам треугольника. Рассмотрим для начала виды треугольников в различии от их углов.
Определение 4
Треугольник будем называть остроугольным, если все углы в нем менее $90^0$.
Определение 5
Треугольник будем называть тупоугольным, если один из углов в нем более $90^0$.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Определение 6
Треугольник будем называть прямоугольным, если один из углов в нем равен $90^0$.
Все эти виды изображены на рисунке 2.
По сторонам треугольники разделяются на разносторонние, равнобедренные и равносторонние.
Определение 7
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Определение 8
Треугольник будем называть равносторонним, если три его стороны будут равны между собой.
Все эти виды треугольников изображены на рисунке 3.
Свойства треугольников
Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.
Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.
Определение 9
Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.
Определение 10
Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.
Определение 11
Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.
Теорема 1
Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.
Теорема 2
Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.
Теорема 3
Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.
Следующие две теоремы рассматривают свойства для равнобедренных треугольников.
Теорема 4
Углы при основании равнобедренного треугольника будут равными.
Теорема 5
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Замечание 1
Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.
Пример задачи
Пример 1
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.
Треугольник, его виды и свойства
Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Медиа́на треуго́льника ) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота в треугольниках различного типа
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
Классификация треугольников (по углам)
Треугольник
Сторона, противоположная прямому углу, называется гипотенузой сторона c. Стороны, прилегающие к прямому углу, называются катетами (b и a). 
Свойства прямоугольного треугольника:
Сумма острых углов треугольника равна 90:
Гипотенуза прямоугольного треугольника больше каждого их катетов:
Катет, лежащий против угла 30о, равен половине гипотенузы.
Если катет в два раза меньше гипотенузы, то он лежит против угла в 30
Две высоты прямоугольного треугольника совпадают с его катетами.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, равна ее половине и является радиусом описанной окружности этого треугольника.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Длина высоты, проведенной к гипотенузе, равна отношению произведения катетов к гипотенузе:

Высота, проведенная к гипотенузе, — есть среднее пропорциональное между отрезками, на которые она делит гипотенузу:
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу (И ОТРЕЗКОМ ГИПОТЕНУЗЫ, ЗАКЛЮЧЕННЫМ МЕЖДУ КАТЕТОМ И ВЫСОТОЙ):
Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
Признаки прямоугольного треугольника
(Теорема, обратная теореме Пифагора)
Если квадрат стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник — прямоугольный.
Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник — прямоугольный.
Если центр описанной окружности лежит на стороне треугольника, то этот треугольник — прямоугольный. (Сторона, на которой лежит центр описанной около данного треугольника окружности, является гипотенузой).
Если радиус окружности, описанной около треугольника, равен половине его стороны, то этот треугольник прямоугольный.
(Если радиус равен половине стороны, то диаметр равен стороне. Значит, угол, лежащий напротив этой стороны — прямой
Если в треугольнике сумма двух острых углов равна 900, то треугольник прямоугольный.
Классификация треугольников (по сторонам)
Треугольник

Две равные стороны равнобедренного треугольника называются боковыми, третья сторона — основанием.
Свойства равнобедренного треугольника
Углы при основании равны.
Равны биссектрисы, проведённые из углов при основании. Равны медианы, проведённые из углов при основании. Равны высоты, проведённые из углов при основании.
Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой.
Центры вписанной и описанной окружностей лежат на этой линии.
Верно и обратное: если в треугольнике две медианы (две биссектрисы или две высоты) равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.

Свойства равностороннего треугольника
Все стороны правильного треугольника равны между собой,
Все углы также равны и составляют 60°.
Все высоты, медианы и биссектрисы совпадают.
Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Центры вписанной и описанной окружностей СОВПАДАЮТ
1 часть (прямоугольный треугольник)
1. У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
2. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
3. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.
4. В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.
5. Медиана равностороннего треугольника равна ![]() . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
6. В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() — медиана,
— медиана, ![]() . Найдите
. Найдите ![]() .
.
7. В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.
8.В треугольнике ![]() известно, что AM=31,
известно, что AM=31, ![]() — медиана,
— медиана, ![]() . Найдите AC.
. Найдите AC.
9. Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
10. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 8, AC = 32.
11. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
12. От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.

13. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
14. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
15. Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?
16. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут?
17. Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.
18. Лестница соединяет точки A и B и состоит из 35 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).

19. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
20. Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
21 Периметр равнобедренного треугольника ABC c основанием AC равен 63 см. Медиана BM образует со стороной BC Найдите АС.

22. Лестница соединяет точки A и B. Высота каждой ступени равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет 10 м. Найдите высоту, на которую поднимается лестница (в метрах).
2 часть (равнобедренный треугольник)

1. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите ![]() .
.
2. В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите ![]()

3. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
4. В треугольнике ABC AC = BC. Угол при вершине Cравен 146°. Найдите внешний угол при вершине B. Ответ дайте в градусах.
5. Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
6. Высота равностороннего треугольника равна ![]() Найдите его периметр.
Найдите его периметр.
7. В треугольнике ABC AB = BC = 53, AC = 56. Найдите длину медианы BM.
8. В треугольнике ![]() известно, что
известно, что ![]() ,
, ![]() . Найдите угол
. Найдите угол ![]() . Ответ дайте в градусах.
. Ответ дайте в градусах.
9. Сторона равностороннего треугольника равна ![]() . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника.
Список литературы
Википедия – свободная энциклопедия https://ru.wikipedia.org/wiki/Заглавная_страница
Решу ОГЭ – образовательный портал для подготовки к экзаменам https://oge.sdamgia.ru
Òèïû òðåóãîëüíèêîâ â çàâèñèìîñòè êîëè÷åñòâà ðàâíûõ ñòîðîí.
Íåêîòîðûé òðåóãîëüíèê, â êîòîðîì âñå ñòîðîíû íå îäèíàêîâîé äëèíû, ïðèíÿòî íàçûâàòü ðàçíîñòîðîííèìè.
Òðåóãîëüíèê, ñ äâóìÿ îäèíàêîâûìè ñòîðîíàìè îáîçíà÷àþò êàê ðàâíîáåäðåííûé. Îäèíàêîâûå ñòîðîíû ïðèíÿòî èìåíîâàòü áîêîâûìè, òðåòüþ ñòîðîíó — îñíîâàíèåì.  ðàâíîé ìåðå áóäåò âåðíûì è òàêîå îïðåäåëåíèå îñíîâàíèÿ òðåóãîëüíèêà — ýòî ñòîðîíà ðàâíîáåäðåííîãî òðåóãîëüíèêà, êîòîðàÿ íå ðàâíà äâóì äðóãèì ñòîðîíàì.
 ðàâíîáåäðåííîì òðåóãîëüíèêå óãëû ïðè îñíîâàíèè ðàâíîâåëèêè. Âûñîòà, ìåäèàíà, áèññåêòðèñà ðàâíîáåäðåííîãî òðåóãîëüíèêà, ïðî÷åð÷åííûå ê åãî îñíîâàíèþ, ñîâìåùàþòñÿ.
Òðåóãîëüíèê, ñî âñåìè îäèíàêîâûìè ñòîðîíàìè, îáîçíà÷àþò êàê ðàâíîñòîðîííèå èëè ïðàâèëüíûå.  ðàâíîñòîðîííåì òðåóãîëüíèêå âñå óãëû ïî 60°, à öåíòðû âïèñàííîé è îïèñàííîé îêðóæíîñòè ñîâìåùåíû.
Òèïû òðåóãîëüíèêîâ â çàâèñèìîñòè îò ïàðàìåòðîâ óãëîâ.
Òðåóãîëüíèê, â êîòîðîì òîëüêî óãëû ìåíüøå 900 (îñòðûå), èìåíóþò îñòðîóãîëüíûì.
Òðåóãîëüíèê, â êîòîðîì ïðåäñòàâëåí óãîë 900, èìåíóþò ïðÿìîóãîëüíûì. Ñòîðîíû òðåóãîëüíèêà, ôîðìèðóþùèå ïðÿìîé óãîë, ïðèíÿòî îáîçíà÷àòü êàòåòàìè, à ñòîðîíà ðàñïîëîæåííàÿ íàïðîòèâ ïðÿìîãî óãëà — ãèïîòåíóçîé.
Òðåóãîëüíèê, â êîòîðîì ïðèñóòñòâóåò óãîë áîëåå 900 (òóïîé óãîë) , èìåíóåòñÿ òóïîóãîëüíûì.
Ðàñ÷åò òðåóãîëüíèêà îíëàéí | |
| Ðàñ÷åò âñåõ óãëîâ, ñòîðîí è ïëîùàäè ïî èçâåñòíûì óãëàì è ñòîðîíàì òðåóãîëüíèêà, ÷åðòåæ òðåóãîëüíèêà | |
| Ðàñ÷åò òðåóãîëüíèêà îíëàéí | |
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Òðåóãîëüíèê | |
| Òðåóãîëüíèê, ñòîðîíû, óãëû, âûñîòà òðåóãîëüíèêà, ìåäèàíû, áèññåêòðèñû. Ïðÿìîóãîëüíûé òðåóãîëüíèê, ïëîùàäü òðåóãîëüíèêà. | |
| Òðåóãîëüíèê | |
Треугольник
Треугольник — это замкнутая ломаная, состоящая из трех звеньев, и часть плоскости, ею ограниченная.
В дальнейшем используются следующие обозначения:
a ,b, c — длины сторон DC, AC, AB треугольника ABC соответственно;
![]() — полупериметр треугольника ABC;
— полупериметр треугольника ABC;
Неравенство треугольника — в любом треугольнике сумма длин двух сторон больше длины третьей стороны: a + b c, b +c a, a + c b
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
Теорема. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине: ![]() ,
, ![]() .
.
Пусть c — наибольшая из трех сторон треугольника, тогда: если c² a² + b² , то треугольник остроугольный; если, c² = a² +b², то треугольник прямоугольный; если c² a² +b² , то треугольник тупоугольный.
Теорема. Сумма углов треугольника равна ![]() :
: ![]() .
.
Следствие: В треугольнике не может быть более одного тупого или прямого угла.
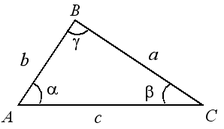
Внешний угол — угол, смежный с каким-нибудь углом треугольника.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
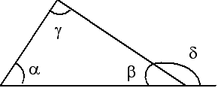
Теорема синусов. Отношение длины стороны треугольника к синусу противолежащего угла для данного треугольника есть величина постоянная и равная диаметру описанной около треугольника окружности: ![]()
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: ![]() .
.
Теорема. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине: ![]() ,
, ![]() .
.
Высота — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Высоты треугольника пересекаются в одной точке, называемой ортоцентром. Длины высот находятся по следующим формулам: ![]() ,
, ![]() .
.
Серединный перпендикуляр к отрезку — прямая, перпендикулярная к этому отрезку и проходящая через его середину.
Теорема. Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от его концов.
Верно и обратное утверждение: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.
Все три серединных перпендикуляра пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника.
Если треугольник остроугольный, центр описанной окружности лежит строго внутри треугольника. Если треугольник прямоугольный, центр описанной окружности лежит на середине гипотенузы. Если треугольник тупоугольный, центр описанной окружности лежит вне треугольника.
Радиус описанной окружности может быть найден по формулам: ![]() ,
, ![]() .
.
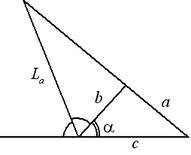
Биссектриса треугольника
Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол на две равные части.
Биссектрисой угла треугольника называется отрезок биссектрисы угла, соединяющий вершину треугольника с точкой противолежащей стороны.
Теоремы:
Биссектриса угла треугольника — множество точек, равноудаленных от сторон угла.
Биссектриса делит сторону, к которой она проведена на отрезки, пропорциональные боковым сторонам: ![]() .
.
Точкой пересечения биссектрисы делятся в отношении суммы сторон треугольника, образующих угол, в котором проведена биссектриса, к третьей стороне: ![]() .
.
Длина биссектрисы равна: ![]() .
.
Биссектрисы треугольника пересекаются в одной точке, являющейся центром вписанной в треугольник окружности. Радиус вписанной окружности может быть найден по формулам: ![]()
Медиана треугольника
Медиана — отрезок, соединяющий вершину треугольника с серединой ее противоположной стороны.
Теоремы:
Медиана, проведенная из вершины треугольника, делит его на два равновеликих: ![]() .
.
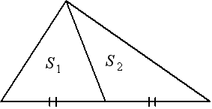
Медианы пересекаются в одной точке, называемой центроидом треугольника, и точкой пересечения делятся в отношении 2:1 считая от вершины.
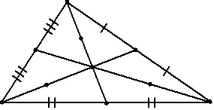
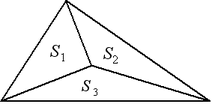
Отрезки медиан, соединяющие вершины с центроидом, делят треугольник на три равновеликих: ![]() .
.
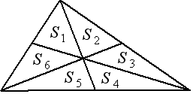
Пересекаясь, медианы делят треугольник на шесть равновеликих: ![]() .
.
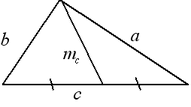
Длина медианы, проведенной к стороне ![]() равна:
равна: ![]() .
.
Признаки равенства и подобия треугольников
Признаки равенства треугольников
Теорема (первый признак равенства треугольников).
Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.
Теорема (второй признак равенства треугольников).
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема (третий признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Признаки подобия треугольников
Подобными называются треугольники, у которых углы равны, а сходственные стороны пропорциональны: ![]() ,
, ![]() , где
, где ![]() — коэффициент подобия.
— коэффициент подобия.
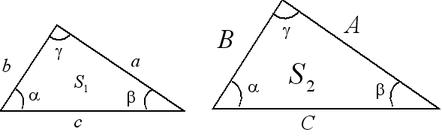
I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
II признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
III признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следствие: Площади подобных треугольников относятся как квадрат коэффициента подобия: ![]() .
.
Равносторонний треугольник и его свойства
Равносторонний треугольник — треугольник, у которого все стороны равны: ![]() .
.
Теоремы:
Все углы равностороннего треугольника равны
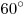 :
: 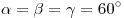 .
.Медианы, биссектрисы и высоты равностороннего треугольника совпадают и равны
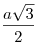 :
: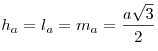 .
.Радиус описанной вокруг равностороннего треугольника окружности:
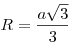 .
.Радиус вписанной в равносторонний треугольник окружности:
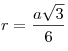 .
.Площадь равностороннего треугольника:
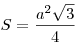 .
.
Равнобедренный треугольник и его свойства
Равнобедренный треугольник — треугольник, у которого две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона — основанием треугольника.
Теоремы:
Углы при основании равны:
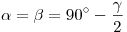 .
.Медиана, проведенная к основанию, является биссектрисой и высотой:
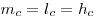 .
.Площадь равнобедренного треугольника:
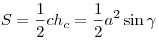 .
.
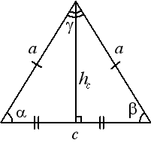
Прямоугольный треугольник и его свойства
Теорема Пифагора: .
Решение прямоугольного треугольника:
;
;
.
Теоремы:
Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки: . Эти отрезки являются проекциями катетов на гипотенузу.
Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу: .
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на два подобных и подобных исходному треугольнику
Длина высоты, проведенной из вершины прямого угла, равна отношению произведения длин катетов и гипотенузы: .
Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы: .
Радиус вписанной окружности равен половине суммы катетов, уменьшенной на гипотенузы: .
Площадь прямоугольного треугольника равна половине произведения катетов: или вычисляется по любой из формул для вычисления площади произвольного треугольника.
Формулы для вычисления площади треугольника
Площадь треугольника равна: .
Площадь треугольника равна: .
Формула Герона: .
Площадь треугольника равна: .
Площадь треугольника равна: .
Если в треугольнике одну из сторон изменить в ![]() раз, а другую в раз, оставив без изменения угол между ними, то площадь получившегося треугольника изменится в раз.
раз, а другую в раз, оставив без изменения угол между ними, то площадь получившегося треугольника изменится в раз.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения длин сторон, заключающих равные углы.
