Какие бывают свойства умножения
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42
4 · 2 · 3 = 3 · 2 · 4 = 24
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c)
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Илья Маслюков · 15 ноября 2018
8,3 K
Выпускник экономического вуза, мама двоих детей, фрилансер, таролог в пути)…
Распределительное свойство умножения выглядит так:
(a+b)*c=ac+bc
(a-b)*c=ac-bc
Для того, чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить.
Для того, чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе.
Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
С помощью букв распределительное свойство умножения относительно сложения записывают так:
a*(b+c)=a*b+a*c
либо так:
(b+c)*a=a*b+a*c
Существует ли какое-то доказательство того, почему работает закон умножения а*б=б*а (где а и б — действительные числа), или это принимается как аксиома?
На самом деле может быть и так, и так. Умножение можно определить двумя способами. 1) существует такая аксиоматика Пеано, которая сначала определяет, что такое натуральные числа и ноль и вводит для них две операции: сложения и умножения. Умножение определяется сначала для нуля a*0=0, а затем индуктивно для всех n: a*(n+1)=a*n+a. После аксиом и определений начинаются теоремы, где доказывается коммутативность a•b=b•a для натуральных чисел с нулем. Делается это методом математической индукции. Но это лишь для натуральных. Затем опреледляются целые числа (добавили отрицательных). Для них расширяется понятие сложения и умножения, и снова доказываются все теоремы, включая коммутативность умножения, но уже для целых. Это не всё. Теперь очередь рациональных чисел. Снова определение умножения и сложения и снова доказательство новой расширенной операции, что она коммутативна. Следующими приходят на очередь действительные числа как множество пополнения (фундаментальные последовательности и все такое, если нужны подробности) для рациональных. И да, снова расширение для сложения и умножения, снова доказательство коммутативности. Далее можно продолжить на комплексные. 2) Но есть и другой подход. Действительные числа определяются как непрерывное упорядоченное поле, то есть задаются аксиомы поля (Группа коммутативная по сложению, Группа коммутативная по умножению без нуля, дистрибутивность), аксиомы упорядоченности (например, что из a < b следует a + c < b + c), и аксиома непрерывности Дедекинда (что если элементы множества A целиком меньше или равны элементам множества B, то есть число, которое больше или равно любого элемента A, а также меньше или равно любого элемента B). И вот в такой системе аксиом коммутативность умножения a•b=b•a является аксиомой: без нуля все числа являются коммутативной группой по умножению, а, значит, операция умножения коммутативна из определения коммутативной группы. И да, существует теорема, которая доказывает, что такое непрерывное упорядоченное поле может быть только одно и оно совпадает с тем, что дают нам аксиомы Пеано и все последующее их обобщения до действительных чисел (более формально: они изоморфны относительно сложения, умножения и упорядоченности)
Итого, если действительные числа — это расширение натуральных-целых-рациональных, то a•b=b•a — теорема. Если действительные числа — это поле, то a•b=b•a — аксиома
P. S. Комплексные числа и в той, и в той аксиоматике определяются как расширение действительных одинаково. Заново в них определяется умножение. Но его коммутативность доказать несложно, используюя коммутативность умножения действительных чисел.
Прочитать ещё 4 ответа
Как выучить таблицу умножения быстро?
Превратите процесс в игру. Например не попить кофе пока не вспомните 7*8, не лягу спатьесли не расскажу всю таблицу. Так появится мотивация. Удачи!)))
Что такое умножение?
можно сразу привести пример …
5 + 5 + 5 = ? вот тут нужно запомнить ( правило ) : цыфры все одинаковые посчитаем сколько раз повторяются пятёрки. у нас три одинаковых пятёрки, значит пять умножаем на три раза. 5 * 3 = 15
( * знак умножения ) ( но нужно ещё знать таблицу умножения! )
((( Без знания таблицы умножения невозможно успешно здать ни ГИА ни ЕГЭ! ))) так что дети, учите!
Почему умножение и деление приоритетнее сложения и вычитания?
Математик, преподаватель, программист
Складывать, вычитать, умножать можно, как известно, не только числа, но и многие другие объекты – векторы, матрицы, тензоры, функции и так далее. Если какой-то объект получается из других сложением и умножением, то часто его удобно представить в виде суммы произведений: например, (a+b)x+d = ax+bx+d. Второе выражение, хоть и содержит больше букв, имеет стандартный вид, такие выражения проще складывать, умножать и вообще понимать. Многие при изучении математики встречались с такими выражениями: стандартный вид многочлена, линейные уравнения, разложение вектора по базису, степенные ряды, включая ряды Тейлора, ограничения и целевые функции в задачах линейного программирования, формула полной вероятности и тому подобное. (Важнейший случай такой суммы, в которой все произведения из двух множителей, и первые множители – числа, называется линейной комбинацией). Получается, сумма произведений настолько универсальна, что выражение без скобок «по умолчанию» читается как сумма произведений: ax+bx+d = (ax)+(bx)+d.
С другой стороны, сложение и умножение (почти любые) ассоциативны, то есть выполняются законы a+(b+c)=(a+b)+c и a(bc)=(ab)c. Это позволяет выполнять операции, учитывая приоритет, в любом порядке: наш пример, если удобно, мы можем посчитать как ax+(bx+d), а если бы приоритета не было, выражение «читалось» бы слева направо как (((ax)+b)x)+d, а справа налево как a(x+(b(x+d))), и это два разных выражения. А читать справа налево, как и переставлять члены, приходится часто.
Вычитание же – операция, обратная сложению, а деление – обратная умножению, поэтому приоритеты у них те же. Впрочем, в серьёзной математической литературе (кроме школьной) вы вряд ли встретите знак деления, вместо него скорее дробь или возведение в минус первую степень.
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
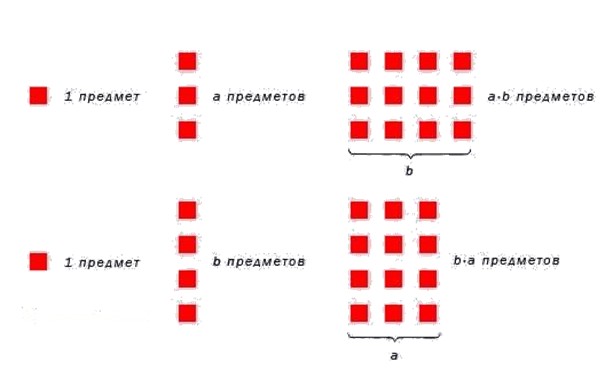
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a·b=b·a
a и b — любые натуральные числа.
Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2·6. По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2·6=2+2+2+2+2+2=12. Теперь поменяем множители местами. 6·2=6+6=12. Очевидно, переместительный закон выполняется.
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
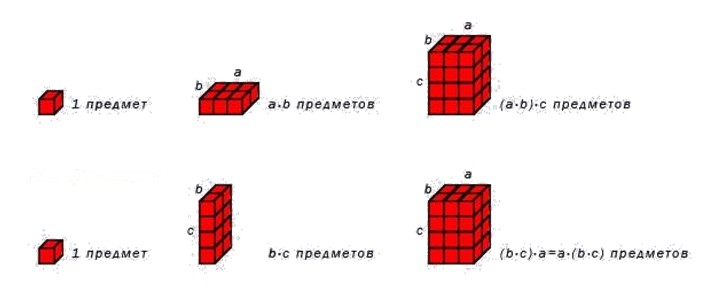
Сочетательное свойство умножения натуральных чисел
Второе название для сочетательного свойства умножения — ассоциативный закон, или ассоциативное свойство. Вот его формулировка.
Сочетательный закон умножения
Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c.
Приведем формулировку в буквенном виде:
a·b·c=a·b·c
a, b, c — любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.
Для наглядности приведем пример. Сначала вычислим значение 4·3·2.
4·3·2=4·6=4+4+4+4+4+4=24
Теперь переставим скобки и вычислим значение 4·3·2.
4·3·2=12·2=12+12=24
4·3·2=4·3·2
Как видим, теория совпадает с практикой, и свойство справедливо.
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
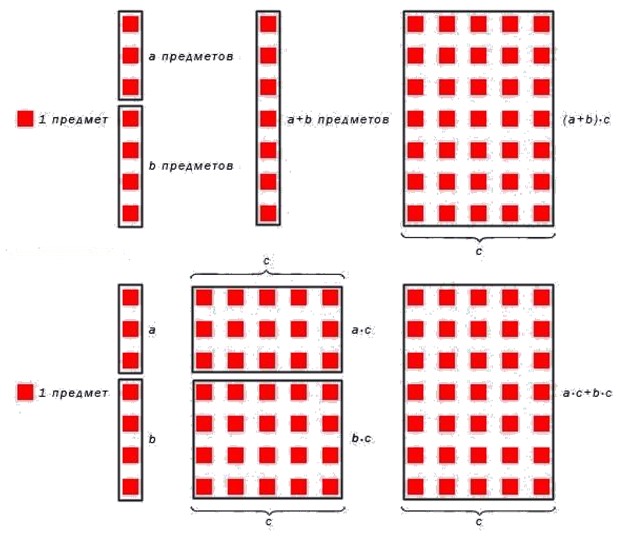
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b+c=a·b+a·c
a, b, c — любые натуральные числа.
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4·3+2.
4·3+2=4·3+4·2=12+8=20
С другой стороны 4·3+2=4·5=20. Справедливость распределительного свойства умножения относительно сложения показана наглядно.
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.

Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b-c=a·b-a·c
a, b, c — любые натуральные числа.
В предыдущем примере заменим «плюс» на «минус» и запишем:
4·3-2=4·3-4·2=12-8=4
С другой стороны 4·3-2=4·1=4. Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.
Умножение единицы на натуральное число
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
1·a=a
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
1·a=∑i=1a1
Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a. Таким образом, переместительное свойство умножения остается справедливым:
1·a=a·1=a
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
Произведение числа 0 и любого натурального числа a равно числу 0.
0·a=0.
По определению, произведение 0·a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0·498=0; 0·9638854785885=0
Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a·0=0.
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
