Какие бывают свойства деления
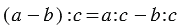
В рамках этой статьи мы изучим общие представления, связанные с делением натуральных чисел. Их принято называть свойствами процесса деления. Мы разберем основные из них, поясним их значение и подкрепим свои рассуждения примерами.
Деление двух равных натуральных чисел
Чтобы понять, как разделить одно натуральное число на другое, равное ему, нужно вернуться к пониманию смысла самого процесса деления. От того, какой смысл мы придаем делителю, зависит конечный результат. Разберем два возможных варианта.
Итак, мы имеем a предметов (a – произвольно взятое натуральное число). Распределим предметы по группам поровну, при этом число групп должно быть равно a. Очевидно, что в каждой группе при этом будет всего один предмет.
Переформулируем немного иначе: как распределить a предметов в группы по a предметов в каждой? Сколько групп получится в итоге? Конечно, всего одна.
Подведем итоги и выведем первое свойство деления натуральных чисел одинаковой величины:
Определение 1
Деление натурального числа на равное ему дает в итоге единицу. Иначе говоря, a: a=1 (a – любое натуральное число).
Разберем для наглядности два примера:
Пример 1
Если 450 разделить на 450, будет 1. Если 67 разделить на 67, получится 1.
Как видно, от конкретных цифр тут ничего не зависит, результат будет один и тот же при условии равенства делимого и делителя.
Деление натурального числа на единицу
Как и в предыдущем пункте, начнем с задач. Допустим, что у нас имеются любые предметы в количестве, равном a. Необходимо разделить их на некоторое количество частей по одному предмету в каждой. Понятно, что у нас выйдет a частей.
А если мы спросим: сколько предметов будет в группе, если в нее поместить a предметов? Ответ очевиден – a.
Таким образом, мы подходим к формулированию свойства деления натуральных чисел на 1:
Определение 2
При делении любого натурального числа на единицу получится то же самое число, то есть a:1=a.
Разберем 2 примера:
Пример 2
Если разделить 25 на 1, получится 25.
Пример 3
Если разделить 11 345 на 1, результатом будет 11 345.
Отсутствие переместительного свойства для деления натуральных чисел
В случае с умножением мы свободно можем поменять множители местами и получить тот же результат, однако на деление это правило не распространяется. Менять местами делимое и делитель можно только в случае, если они являются равными натуральными числами (это свойство мы уже рассматривали в первом пункте). То есть можно сказать, что переместительное свойство распространяется только на случай, если в делении участвуют равные натуральные числа.
В остальных случаях менять местами делимое с делителем нельзя, поскольку это приведет к искажению результата. Объясним подробнее, почему.
Разделять любые натуральные числа на другие, также произвольно взятые, мы можем не всегда. Например, если делимое меньше делителя, то такой пример решить мы не можем (как делить натуральные числа с остатком, мы разберем в отдельном материале). Иными словами, если некоторое натуральное число, равное a, мы можем разделить на b? И их значения при этом не равны, то a будет больше b, а запись b:a смысла иметь не будет. Выведем правило:
Определение 3
В общем случае переместительное свойство на деление натуральных чисел не распространяется, т.е. a: b ≠ b: a (a и b здесь – произвольно взятые натуральные числа, не равные друг другу).
Деление суммы 2-х натуральных чисел на другое натуральное число
Чтобы лучше объяснить это правило, возьмем наглядные примеры.
У нас есть группа детей, между которыми надо поровну разделить мандарины. Фрукты сложены в два пакета. Возьмем условие, что количество мандаринов таково, что можно поделить их на всех детей без остатка. Можно пересыпать мандарины в один общий пакет, а потом поделить и раздать. А можно поделить сначала фрукты из одного пакета, а потом из другого. Очевидно, что и в том, и в другом случае никто не будет в обиде и все будет разделено поровну. Следовательно, мы можем сказать:
Определение 4
Результат деления суммы 2-х натуральных чисел на другое натуральное число равен результату сложения частных от деления каждого слагаемого на то же натуральное число, т.е. (a + b): c = a: c + b: c. При этом значения всех переменных – это натуральные числа, значение a можно разделить на c, и b также можно разделить на c без остатка.
У нас получилось равенство, в правой части которого первым выполняется деление, а вторым – сложение (вспомним, как правильно выполнять арифметические действия по порядку).
Докажем справедливость получившегося равенства на примере.
Пример 4
Возьмем для него подходящие натуральные числа: (18+36):6=18:6+36:6.
Теперь вычислим и узнаем, верное ли оно. Подсчитаем значение левой части: 18+36=54, и (18+36):6=54:6.
Результат мы помним из таблицы умножения (если забыли, найдите в ней нужное значение): 54:6=9.
Далее считаем правую часть: 18:6+36:6.
Вспоминаем, сколько будет 18:6=3 и 36:6=6. Значит, 18:6+36:6=3+6=9.
Получается верное равенство: (18+36):6=18:6+36:6.
Сумма натуральных чисел, которая стоит в примере в качестве делимого, может быть не только 2, но и 3 и больше. Это свойство в комбинации с сочетательным свойством сложения натуральных чисел дает нам возможность выполнять и такие подсчеты.
Пример 5
Так, (14+8+4+2):2 будет равно 14:2+8:2+4:2+2:2.
Деление разности 2-х натуральных чисел на другое натуральное число
Подобным образом можно вывести правило для разности натуральных чисел, которую мы будем делить на другое натуральное число:
Определение 5
Результат деления разности двух натуральных чисел на третье равен тому, что мы получим, отняв от частного уменьшаемого и третьего числа частное вычитаемого и третьего числа.
Т.е. (a-b): c=a: c – b: c. Значения переменных – натуральные числа, при этом a больше b или равно ему, a и b можно разделить на c.
Докажем справедливость этого правила на примере.
Пример 6
Подставим подходящие значения в равенство и вычислим: (45-25):5=45:5-25:5. 45-25=20 (о том, как находить разность натуральных чисел, мы уже писали ранее). (45-25):5=20:5.
По таблице умножения вспоминаем, что результат будет равен 4.
Считаем правую часть: 45:5-25:5. 45:5=9, а 25:5=5, в итоге 45:5-25:5=9-5=4. 4=4, выходит, что (45-25):5=45:5-25:5 – верное равенство.
Деление произведения двух натуральных чисел на другое натуральное число
Вспомним о том, какая связь существует между делением и умножением, тогда свойство деления произведения на натуральное число, равное одному из множителей, будет нам очевидно. Выведем правило:
Определение 6
Если разделить произведение двух натуральных чисел на третье, равное одному из множителей, в итоге мы получим число, равное другому множителю.
В буквенном виде это можно записать как (a·b): a=b или (a·b):b=a (значения a и b представляют собой натуральные числа).
Пример 7
Так, результат деления произведения 2 и 8 на 2 будет равен 8, а (3·7):7=3.
А как быть в случае, если делитель не равен ни одному из множителей, которые образуют делимое? Тогда здесь действует другое правило:
Определение 7
Результат деления произведения двух натуральных чисел на третье натуральное число равен тому, что получится, если разделить на это число один из множителей и результат умножить на другой множитель.
Мы получили весьма неочевидное на первый взгляд утверждение. Однако если учесть, что умножение натуральных чисел, по сути, сводится к сложению равных по значению слагаемых (см. материал об умножении натуральных чисел), то можно вывести этой свойство из другого, о котором мы говорили чуть выше.
Запишем это правило в буквенном виде (значения всех переменных – натуральные числа).
Если a мы можем разделить на c, то будет верно (a·b):c=(a:c) ·b.
Если b делится на c, то верно (a·b):c=a·(b:c).
Если и a, и b делятся на c, то можем приравнять одно равенство к другому: (a·b):c=(a:c) ·b=a·(b:c).
С учетом рассмотренного выше свойства деления произведения на другое натуральное число будут верны равенства (8·6):2= (8:2) ·6 и (8·6):2=8· (6:2).
Мы можем записать их в виде двойного равенства: (8·6):2= (8:2) ·6=8· (6:2).
Деление натурального числа на произведение 2-х других натуральных чисел
И вновь мы начнем с примера. У нас есть некоторое количество призов, обозначим его a. Их надо поровну распределить между участниками команд. Обозначим число участников буквой c, а команд – буквой b. При этом возьмём такие значения переменных, при которых запись деления будет иметь смысл. Задачу можно решить двумя разными способами. Рассмотрим оба.
1. Можно вычислить общее количество участников, умножив b на c, после чего разделить все призы на полученное число. В буквенном виде это решение можно записать как a:(b·c).
2. Можно поделить сначала призы на количество команд, а потом распределить их внутри каждой команды. Запишем это как (a:b):c.
Очевидно, что оба способа дадут нам идентичные ответы. Поэтому оба равенства мы можем приравнять друг к другу: a:(b·c)=(a:b):c. Это и будет буквенная запись свойства деления, которое мы рассматриваем в этом пункте. Сформулируем правило:
Определение 8
Результат деления натурального числа на произведение равен числу, которое мы получим, разделив это число на один из множителей и получившееся частное разделить на другой множитель.
Пример 8
Приведем пример задачи. Докажем, что справедливо равенство 18:(2·3) = (18:2):3.
Подсчитаем левую часть: 2·3=6, а 18:(2·3) – это 18:6=3.
Считаем правую часть: (18:2):3. 18:2=9, а 9:3=3, тогда (18:2):3=3.
У нас получилось, что 18:(2·3)=(18:2):3. Это равенство иллюстрирует нам свойство деления, которое мы привели в данном пункте.
Деление нуля на натуральное число
Что такое нуль? Ранее мы условились, что он означает отсутствие чего-либо. Нуль мы не относим к натуральным числам. Получается, что, если мы разделим нуль на натуральное число, это будет равнозначно попытке разделить пустоту на части. Понятно, что в итоге мы все равно получим «ничто», на сколько бы частей мы его не делили. Выводим отсюда правило:
Определение 9
При делении нуля на любое натуральное число мы получим нуль. В буквенном виде это записывается как 0: a=0, при этом значение переменной может быть любое.
Пример 9
Так, например, 0:19=0, и 0:46869 тоже будет равно нулю.
Деление натурального числа на нуль
Это действие выполнить нельзя. Давайте выясним, почему именно.
Возьмем произвольное число a и предположим, что его можно разделить на 0 и получить в итоге некое число b. Запишем это как a:0=b. Теперь вспомним, как связано между собой умножение и деление, и выведем равенство b·0=a, которое также должно быть справедливым.
Но ранее мы уже поясняли свойство умножения натуральных чисел на ноль. Согласно ему b·0=0. Если сопоставить полученные равенства, у нас получится, что a=0, а это противоречит исходному условию (ведь нуль не является натуральным числом). Выходит, что у нас получилось противоречие, которое доказывает невозможность такого действия.
Определение 10
Делить натуральное число на нуль нельзя.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Деление натуральных чисел
Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.
Рассмотрим задачу:
У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?
Пусть x яблок досталось каждому кролику, тогда мы можем сказать, что общее количество яблок равно: 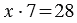 . Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно — это 4:
. Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно — это 4: 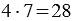 — верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
— верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением.
Данное действие записывают так: 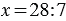 ,
, 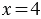 или
или 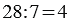 , где:
, где:
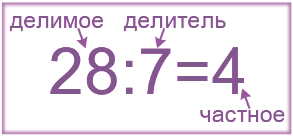
Запомните:
Делимое — это то число, которое делят. Делитель — это то число, на которое делят. Частное — это результат деления.
Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.
Из вышесказанного мы можем сделать вывод:
1. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
Пример: 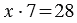 , следовательно,
, следовательно, 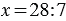 , то есть
, то есть 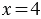 .
.
2. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Пример: 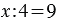 , по смыслу деления
, по смыслу деления 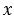 — это произведение 4 и 9, следовательно,
— это произведение 4 и 9, следовательно, 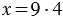 , то есть
, то есть 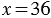 .
.
3. Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Пример: 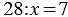 , по смыслу деления число 28 — это произведение множителей
, по смыслу деления число 28 — это произведение множителей 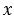 и 7, то есть мы можем записать:
и 7, то есть мы можем записать: 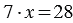 , теперь, применяя пункт 1, получаем:
, теперь, применяя пункт 1, получаем: 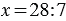 , то есть
, то есть 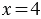 .
.
Свойства деления
Распределительные свойства:
1. Деление суммы на число: 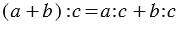
2. Деление разности на число: 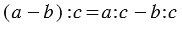
3. Деление произведения на число: 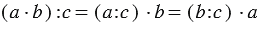
4. Деление числа на произведение: 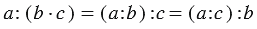
Действия с единицей и нулем
1. Деление числа на единицу: 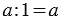 то есть,при делении числа на единицу получается само число
то есть,при делении числа на единицу получается само число
2. Деление числа на себя: 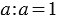 , то есть при делении числа, не равного нулю, на само себя получается единица.
, то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число: 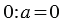 , то есть при делении нуля на любое число, не равное нулю, получаем ноль.
, то есть при делении нуля на любое число, не равное нулю, получаем ноль.
НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Свойства деления
Распределительные свойства:
1. Деление суммы на число:
У Вани и Маши 3 кролика. Маша нашла 9 яблок, а Ваня — 15. Сколько яблок досталось каждому кролику?
Решение:
а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:
1) 9 + 15 = 24 (я) — собрали Маша и Ваня вместе.
2) 24 : 3 = 8 (я) — досталось каждому кролику.
б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:
1) 9 : 3 = 3 (я) — принесла Маша каждому кролику.
2) 15 : 3 = 5 (я) — принес Ваня каждому кролику.
3) 3 + 5 = 8 (я) — досталось каждому кролику.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.
Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
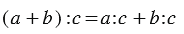
2. Деление разности на число:
Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?
а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:
1) 150 — 72 = 78 (руб.) — осталось после покупки цветов.
2) 78 : 3 = 26 (руб.) — осталось у каждого брата.
б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:
1) 150 : 3 = 50 (руб.) — получил каждый брат.
2) 72 : 3 = 24 (руб.) — потратил каждый брат.
3) 50 — 24 = 26 (руб.) — осталось у каждого брата.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (150 — 72) : 3 = 150 : 3 — 72 : 3.
Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
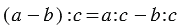
3. Деление произведения на число:
В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?
а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:
1) 12 · 6 = 72 (я) — принесли всего дети.
2) 72 : 3 = 24 (я) — досталось каждому кролику.
б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:
1) 12 : 3 = 4 (чел.) — принесли яблоки 1 кролику.
2) 4 · 6 =24 (я) — досталось каждому кролику.
б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:
1) 6 : 3 = 2 (я) — принес каждый ребенок для одного кролика.
2) 2 · 12 = 24 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.
Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
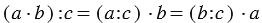
4. Деление числа на произведение:
В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?
а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:
1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:
1) 48 : 4 = 12 (я) — положат в каждую клетку.
2) 12 : 3 = 4 (я) — досталось каждому кролику.
Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:
а) 1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) 1) 48 : 3 = 16 (я) — положат в каждую клетку.
2) 16 : 4 = 4 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4
Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.
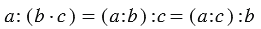
Действия с единицей и нулем
1. Деление числа на единицу:
У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?
Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:
3 : 1 = 3 (я) — достанется кролику, следовательно, мы можем сделать вывод: При делении числа на единицу получается само число: 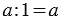
2. Деление числа на себя:
Из свойств умножения мы знаем, что: 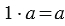 , а мы знаем, что по смыслу деления можно записать, что:
, а мы знаем, что по смыслу деления можно записать, что: 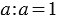 , то есть при делении числа, не равного нулю, на само себя получается единица.
, то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число:
Рассуждая аналогично пункту 2 получаем: 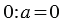 , то есть при делении ноля на любое число, не равное нулю, получаем ноль.
, то есть при делении ноля на любое число, не равное нулю, получаем ноль.
Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Это легко объяснить следующими рассуждениями: пусть мы взяли 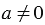 карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по
карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по 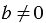 карандашей в каждой коробке:
карандашей в каждой коробке: 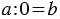 , из смысла деления
, из смысла деления 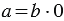 , в то же время мы знаем из свойств умножения, что:
, в то же время мы знаем из свойств умножения, что: 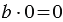 , то есть получаем, что
, то есть получаем, что 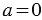 , а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
, а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 702,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1632,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1672,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 426,
Мерзляк, Полонский, Якир, Учебник
Упражнение 486,
Мерзляк, Полонский, Якир, Учебник
Упражнение 3,
Мерзляк, Полонский, Якир, Учебник
Упражнение 5,
Мерзляк, Полонский, Якир, Учебник
Упражнение 633,
Мерзляк, Полонский, Якир, Учебник
Упражнение 1077,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 16,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 28,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 30,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 48,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 66,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 67,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 124,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 273,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 409,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 424,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
