Какая функция называется обратной пропорциональностью свойства функции
Алгебра
Обратная пропорциональность-это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (аргумента) вызывает пропорциональное увеличение, либо уменьшение зависимой величины (функции).
или
где k-любое число,k≠0.
Допустим, мы пришли в магазин за тетрадями. Тетради на прилавке и ваши деньги в кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите тетрадей, тем меньше денег у вас останется.
Графиком функции является гипербола.
График функции при k>0
Гипербола состоит из 2 частей: одна находится в I четверти, где значения X и Yположительные, а вторая часть – в III четверти, где значения X и Yотрицательные.
y(x)>0, при x∈(0;+∞)
y(x)<0, при x∈(0;+∞)
Если двигаться по одной ветви гиперболы от -∞ к 0, то мы замечаем, что функция убывает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы снова видим, что функция убывает. => Функция 
, где K>0, убывает.
График функции при k<0
Гипербола состоит из 2 частей: одна находится во 2 четверти, где значения Xотрицательные, а значения Yположительные, а вторая часть – в 4 четверти, где значения Xположительные, а значения Yотрицательные.
Функция принимает положительное значение на промежутке (-∞;0),
Функция принимает отрицательные значения на промежутке (0;+∞).
Если двигаться по одной ветви гиперболы от -∞ к 0, то мы замечаем, что функция возрастает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы снова видим, что функция возрастает. => Функция , где K<0, Возрастает.
Свойства функции:
1)Область определения функции:
D(f)=(-∞;0)∪(0;+∞).
2)Область значения функции:
E(f)=(-∞;0)∪(0;+∞).
3)Наибольшего и наименьшего значения функция не имеет.
4) — нечетная функция (т.к. 
).
График симметричен относительно начала координат (0;0).
5) Функция не ограничена.
6)Функция не пересекает координатные оси (oX и oY).
Перемещение гиперболы
Если добавить константу а (где a любое число)в знаменатель, в качестве слагаемого к X, то произойдет перемещение гиперболы по оси оX (вместе с вертикальной асимптотой).
В таком случае уравнением функции станет:
Если у а стоит знак «+» (
), то график функции передвигается по оси oX влево.
Для примера возьмем уравнение 
Гипербола смещена на 2 влево.
Если у а стоит знак «–» (
), то график функции передвигается по оси oX вправо.
Для примера возьмем уравнение 
Гипербола смещена на 2 вправо.
Если добавить константу b (где b любое число) к дроби в качестве слагаемого, то произойдет перемещение гиперболы по оси oY (вместе с горизонтальной асимптотой)
В таком случае уравнением функции станет: 
Если у b стоит знак «+» (
), то график функции передвигается по оси oY вверх.
Для примера возьмем уравнение 
Если у b стоит знак «-» (
), то график функции передвигается по оси oY вниз.
Для примера возьмем уравнение 
Гипербола смещена на 2 вниз.
Сужение и расширение графика относительно начала координат.
От коэффициента K зависит, как будут вести себя ветви гиперболы, относительно начала координат.
Например, сравним 
и 
.
Мы видим, что график функции 
значительно уже графика функции 
=>Чем больше коэффициент K , тем больше расстояние между ветвями гиперболы, относительно начала координат.
Сравним 
и 
.
Мы видим, что график функции 
значительно уже графика функции =>Чем меньше коэффициент K , тем меньше расстояние между ветвями гиперболы, относительно начала координат.
Автор статьи: Мажаров Данила Михайлович
Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна
Вернутся к темам
Представим, что у нас есть тело, движущееся равномерно от города А к городу В. Время, которое наше тело затрачивает на прохождение указанного пути зависит от скорости движения. Предположим, что расстояние между А и В равно 120 м, v – это скорость движения (м/с), а t – это время движения (с). Тогда получим, что
t = 120/v.
Подставим вместо v несколько значений и получим t:
если v = 5, то t = 120/5 = 24; если v = 10, то t = 120/10 = 12;
если v = 20, то t = 120/20 = 6.
Получается, что каждому значению переменной v (v > 0) соответствует единственное значение t. Формулой t = 120/v, где v > 0, задается функция.
Обратной пропорциональностью называется функция, которую можно задать формулой вида у = k/х, где k – не равное нулю число.
Относительно переменной у говорится, что она обратно пропорциональна переменной х.
Т.к. выражение k/х при любом значении х, кроме 0, имеет смысл, то областью определения функции, задаваемой формулой у = k/х, может служить множество всех чисел, отличных от нуля, или какое-нибудь его подмножество.
Из формулы у = k/х следует, что ху = k. Верно и обратное: если ху = k (k ≠ 0), то у = k/х. Логично, что, чтобы выяснить, является ли обратной пропорциональностью функция х – у, необходимо сравнить произведения ху для всех соответственных значений х и у. Если эти произведения равны одному и тому же числу k, где k ≠ 0, то функция f является обратной пропорциональностью.
Определим, является ли обратной пропорциональностью функция m – n, заданная значениями:
если m = 1, то n = 15;
если m = 2, то n = 7,5;
если m = 3, то n = 5;
если m = 5, то n = 3;
если m = 6, то n = 2,5;
если m = 10, то n = 1,5;
если m = 15, то n = 1.
Для каждой пары (m; n) соответственных значений m и n найдем произведение mn:
если m = 1, n = 15, то mn = 15;
если m = 2, n = 7,5, то mn = 15;
если m = 3, n = 5, то mn = 15;
если m = 5, n = 3, то mn = 15;
если m = 6, n = 2,5, то mn = 15;
если m = 10, n = 1,5, то mn = 15;
если m = 15, n = 1, то mn = 15.
В результате получаем, что найденные произведения равны одному и тому же числу 15. Следовательно, функция f – обратная пропорциональность.
Решим задачу.
Пусть а – основание прямоугольника (см), b – его высота (см). Если площадь прямоугольника остается постоянной, то с изменением длины его основания должна изменяться и его высота. Является ли зависимость переменной b от переменной а обратной пропорциональностью?
Для любой пары соответственных значений переменных а и b произведение аb равно одному и тому же числу, выражающему площадь прямоугольника в см2. Следовательно, зависимость b от а – обратная пропорциональность.
Вернемся к примеру с равномерным движением тела из города А в город В. Возьмем два произвольных значения переменной v: v1 = 5 и v2 = 6. Тогда соответствующие им значения переменной t: t1 = 24 и t2 = 20.
Найдем частное v1/v2и частное t1/t2:
v1/v2 = 5/6; t1/t2 = 6/5.
Отметим, что частное v1/v2 равно числу, обратному частному t1/t2. К такому же выводу мы придем, если выберем иные значения переменных.
Т.о., если функция х → у – обратная пропорциональность и (х1; у1), (х2; у2) – пары соответственных значений переменных х и у, то х1/х2 = у2/у1.
Докажем это. Из формулы у = k/х имеем, что у1 = k/х1, у2 = k/х2, причем у1 ≠ 0, у2 ≠ 0. Отсюда
у2/у1 = (k/х2) / (k/х1) = (k/х2) ∙ ( х1/ k) = х1/х2.
Если значения переменных х и у – это положительные числа, то рассмотренное свойство обратной пропорциональности можно определить так:
с увеличением значения х в несколько раз соответствующее значение у уменьшается во столько же раз; аналогично: с уменьшением значения х в несколько раз соответствующее значение у увеличивается во столько же раз.
Применим установленное свойство к решению задач.
Задача.
Велосипедист, двигаясь со скоростью 10 км/ч, проехал расстояние от города А до города В
за 6 ч. Сколько времени затратит велосипедист на обратный путь, если будет двигаться со скоростью 12 км/ч?
Решение.
Пусть на обратный путь велосипедист затратит х ч. Т.к. время, необходимое для прохождения одного и того же расстояния, обратно пропорционально скорости движения, то х/6 = 10/12. Отсюда 12х = 60, х = 5.
Ответ: велосипедисту понадобится 5 ч.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
График какой из приведенных ниже функций изображен на рисунке?
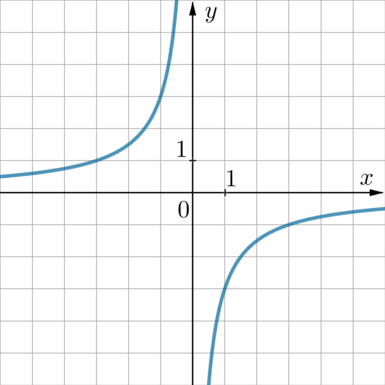
1) (y=dfrac 3xqquad ) 2) (y=-dfrac1{3x}qquad ) 3) (y=dfrac1{3x}qquad ) 4) (y=-dfrac3x)
На рисунке изображена гипербола, уравнение которой имеет вид (y=dfrac kx), причем, так как она находится во 2 и 4 четвертях, то (k<0).
Следовательно, выбираем между 2 и 4.
Данная гипербола проходит, например, через точку (x=-1, y=3). Проверкой убеждаемся, что эта точка удовлетворяет уравнению 4 (подставим: (y=-frac3{-1}=3)).
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
Ответ: 4
График какой из приведенных ниже функций изображен на рисунке?
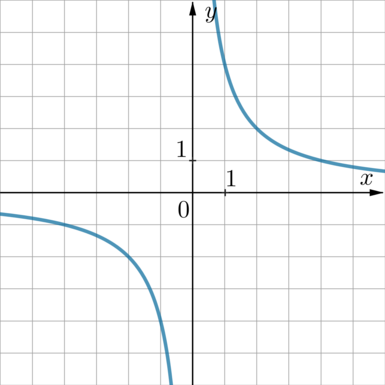
1) (y=dfrac 4xqquad ) 2) (y=-dfrac1{4x}qquad ) 3) (y=-dfrac4{x}qquad ) 4) (y=dfrac1{4x})
На рисунке изображена гипербола, уравнение которой имеет вид (y=dfrac kx), причем, так как она находится в 1 и 3 четвертях, то (k>0).
Следовательно, выбираем между 1 и 4.
Данная гипербола проходит, например, через точку (x=1, y=4). Проверкой убеждаемся, что эта точка удовлетворяет уравнению 1 (подставим (y=frac 41=4)).
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
Ответ: 1
На одном из рисунков изображен график функции (y=dfrac3x). Укажите номер этого рисунка.
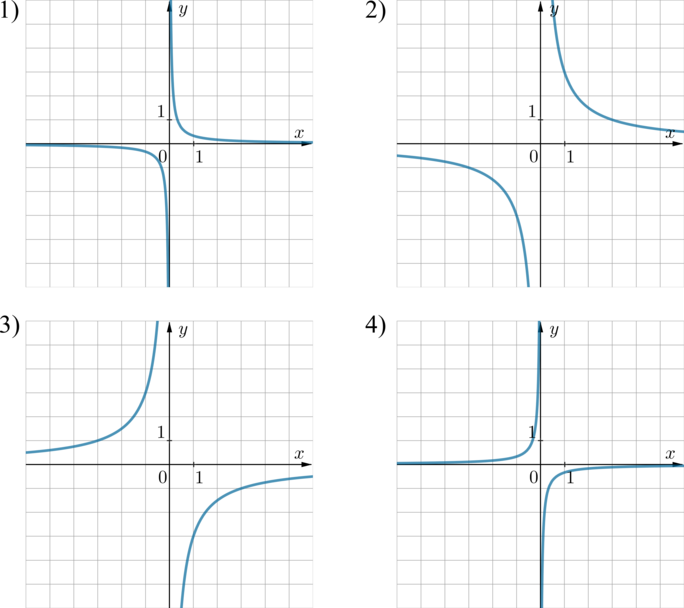
Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. В нашем случае гипербола (y=frac 3x) находится в 1 и 3 четвертях, следовательно, либо картинка 1, либо картинка 2.
Гипербола (y=frac 3x) проходит через точку (x=1, y=3). Через эту точку проходит только гипербола, изображенная на картинке 2.
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
Ответ: 2
На одном из рисунков изображен график функции (y=-dfrac5x). Укажите номер этого рисунка.
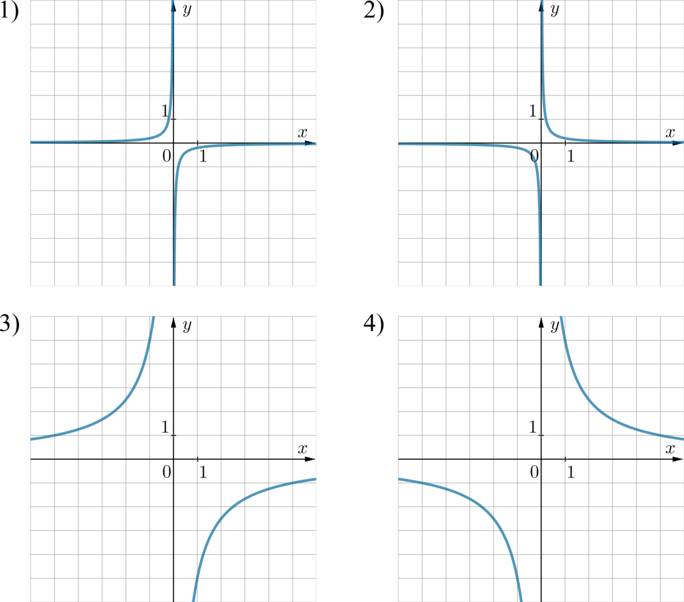
Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. В нашем случае гипербола (y=-frac 5x=frac{-5}x) находится во 2 и 4 четвертях, следовательно, либо картинка 1, либо картинка 3.
Гипербола (y=-frac 5x) проходит через точку (x=-1, y=5). Через эту точку проходит только гипербола, изображенная на картинке 3.
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
Ответ: 3
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ:
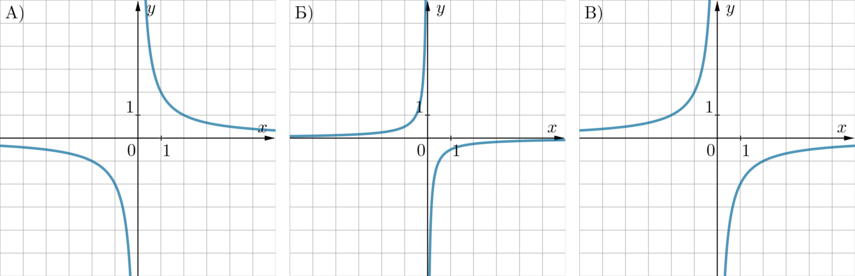
ФОРМУЛЫ:
1) (y=-dfrac 2xqquad ) 2) (y=dfrac2xqquad ) 3) (y=-dfrac1{2x})
В таблице под каждой буквой укажите соответствующий номер.
Ответ: (begin{array}{|c|c|c|} hline text{А} & text{Б} & text{В} \
hline && \ hline end{array})
Способ 1.
Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. Отсюда следует, что гиперболе А, находящейся в 1 и 3 четвертях, соответствует формула 2.
Гипербола В проходит, например, через точку (x=-1, y=2). Эта точка удовлетворяет только формуле 1. Следовательно, В – 1, Б – 3.
Ответ: (begin{array}{|c|c|c|} hline text{А} & text{Б} & text{В} \
hline 2&3&1 \ hline end{array})
В ответ запишем 231.
(Вообще говоря, в одном масштабе чем “плотнее” гипербола (y=frac kx) прижата к осям координат, тем меньше по модулю ее коэффициент (k). Например в нашем случае масштабы всех картинок одинаковы, и на картинке Б гипербола плотнее прижата к осям, следовательно, из двух формул 1 и 3 ей соответствует формула 3, так как в формуле 1 коэффициент (k=-2), а в формуле 3 коэффициент (k=-frac12).)
Способ 2.
Заметим, что формулы 1 и 2 отличаются лишь знаком, это значит, что график, задающийся формулой 2, получается из графика, задающегося формулой 1, отражением относительно горизонтальной оси. Такие графики у нас представлены на картинках А и В. Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. Отсюда однозначно: А – 2, В – 1.
Тогда Б – 3.
Ответ: 231
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ:
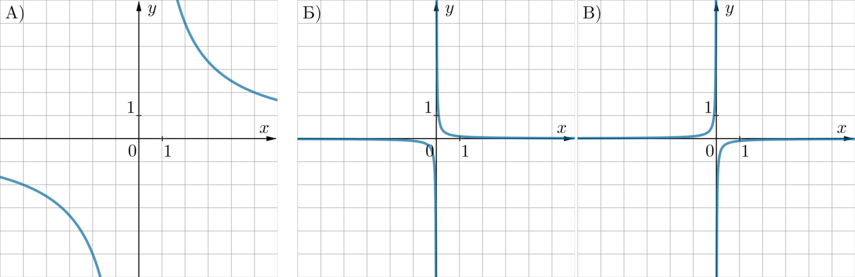
ФОРМУЛЫ:
1) (y=dfrac1{10x}qquad ) 2) (y=-dfrac1{10x}qquad ) 3) (y=dfrac{10}x)
В таблице под каждой буквой укажите соответствующий номер.
Ответ: (begin{array}{|c|c|c|} hline text{А} & text{Б} & text{В} \
hline && \ hline end{array})
Способ 1.
Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. Отсюда следует, что гиперболе В, находящейся в 2 и 4 четвертях, соответствует формула 2.
Гипербола А проходит, например, через точку (x=2, y=5). Эта точка удовлетворяет только формуле 3. Следовательно, А – 3, Б – 1.
Ответ: (begin{array}{|c|c|c|} hline text{А} & text{Б} & text{В} \
hline 3&1&2 \ hline end{array})
В ответ запишем 312.
(Вообще говоря, в одном масштабе чем “плотнее” гипербола (y=frac kx) прижата к осям координат, тем меньше по модулю ее коэффициент (k). Например в нашем случае масштабы всех картинок одинаковы, и на картинке Б гипербола плотнее прижата к осям, следовательно, из двух формул 1 и 3 ей соответствует формула 1, так как в формуле 1 коэффициент (k=frac1{10}), а в формуле 3 коэффициент (k=10).)
Способ 2.
Заметим, что формулы 1 и 2 отличаются лишь знаком, это значит, что график, задающийся формулой 2, получается из графика, задающегося формулой 1, отражением относительно горизонтальной оси. Такие графики у нас представлены на картинках Б и В. Если в уравнении гиперболы (y=frac kx) коэффициент (k>0), то она находится в 1 и 3 четвертях, если (k<0) – во 2 и 4. Отсюда однозначно: Б – 1, В – 2.
Тогда А – 3.
Ответ: 312
Найдите значение (k) по графику функции (y=dfrac kx), изображенному на рисунке.
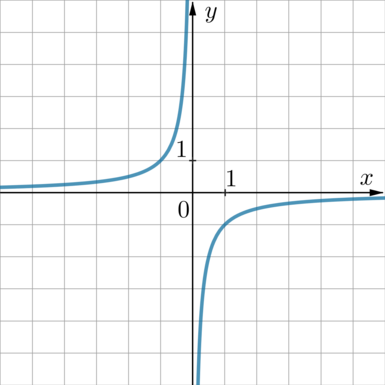
Данная гипербола проходит, например, через точку (x=-1, y=1). Следовательно, имеем: (1=frac k{-1}), откуда (k=-1).
Ответ: -1
1 урок по теме
«Функция обратной пропорциональности и её график».
Выполнила:
Телегина Л.Б.
Цель урока:
- повторить весь изученный материал по функциям.
- ввести определение обратной пропорциональности и научить строить её график.
- развивать логическое мышление.
- воспитывать внимание, аккуратность, точность.
План урока:
- Повторение.
- Объяснение нового материала.
- Физкультминутка.
- Закрепление.
- Подведение итогов, оценки, задание на дом.
Оборудование: плакаты.
Ход урока:
- Урок начинается с повторения. Учащимся предлагается разгадать кроссворд (который заранее подготовлен на большом листе бумаги).
Вопросы кроссворда:
1. Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. [Функция].
2. Независимая переменная. [Аргумент].
3. Множество точек координатной плоскости абсциссы, которых равны значениям аргумента, а ординаты – значениям функции. [График].
4. Функция, заданная формулой y=kx+b. [Линейная].
5. Каким коэффициентом называют число k в формуле y=kx+b? [Угловым].
6. Что служит графиком линейной функции? [Прямая].
7. Если k≠0, то график y=kx+b пересекает эту ось, а если k=0, то параллелен ей. Какой буквой эта ось обозначается? [Икс].
8. Слово в названии функции y=kx? [Пропорциональность].
9. Функция, заданная формулой y=x2. [Квадратичная].
10. Название графика квадратичной функции. [Парабола].
11. Буква латинского алфавита, которой часто обозначают функцию. [Игрек].
12. Один из способов задания функции. [Формула].
Учитель: Какие основные способы задания функции нам известны?
(Один учащийся получает задание у доски: заполнить таблицу значений функции 12/x по данным значениям её аргумента, а затем построить на координатной плоскости соответствующие точки).
х | -12 | -8 | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 |
у |
Остальные отвечают на вопросы учителя: (которые заранее записаны на доске)
1. Как называются следующие функции, заданные формулами: y=kx, y=kx+b, y=x2, y=x3?
2. Укажите область определения следующих функций: y=x2+8, y=1/x-7, y= 4x-1/5, y=2x, y=7-5x, y=2/x, y=x3, y=-10/x.
Затем учащиеся работают по таблице, отвечая на поставленные учителем вопросы:
1. На каком рисунке из таблицы изображены графики:
а) линейной функции;
б) прямой пропорциональности;
в) квадратичной функции;
г) функции вида y=kx3?
2. Какой знак имеет коэффициент k в формулах вида y=kx+b, которым соответствуют графики на рисунках 1, 2, 4, 5 таблицы?
3. Найти в таблице графики линейных функций, у которых угловые коэффициенты:
а) равны;
б) равны по модулю и противоположны по знаку.
(Затем весь класс проверяет, верно ли ученик, вызванный к доске заполнил таблицу и расставил точки на координатной плоскости).
2. Объяснение начинается с мотивации.
Учитель: Как известно, всякая функция описывает какие-то процессы, происходящие в окружающем нас мире.
Рассмотрим, например, прямоугольник со сторонами x и y и площадью 12см2. Известно, что x*y=12, но что будет, если начать изменять одну из сторон прямоугольника, допустим сторону длиной x?
Длину стороны y можно узнать из формулы y=12/x. Если x увеличить в 2 раза, то будет иметь y=12/2x, т.е. сторона y уменьшится в 2 раза. Если значение x увеличить в 3, 4, 5… раз, то значение y во столько же раз уменьшится. Наоборот, если x уменьшать в несколько раз, то y будет увеличиваться во столько же раз. (Работа по таблице).
Поэтому функцию вида y=12/x называют обратной пропорциональностью. В общем виде она записывается так y=k/x, где k-константа, причём k≠0.
Это тема сегодняшнего урока, записали в тетрадях. Даю строгое определение. Для функции y=12/x, являющейся частным видом обратной пропорциональности, мы уже записали в таблице ряд значений аргумента и функции и изобразим соответствующие точки на координатной плоскости. Как же выглядит график данной функции? По построенным точкам трудно судить обо всём графике, ведь точки можно соединить как угодно. Давайте попробуем вместе сделать выводы о графике функции, вытекающие из рассмотрения таблицы и формулы.
Вопросы к классу:
- Какова область определения функции y=12/x?
- Положительны или отрицательны значения y, если
а) x
б) x>0?
3. Как изменяется значение переменной y с изменением значения x?
Итак,
- точка (0,0) не принадлежит графику, т.е. он не пересекает ни оси OX, ни оси OY;
- график находится в Ι и ΙΙΙ координатных четвертях;
- плавно приближается к координатным осям как в Ι координатной четверти, так и в ΙΙΙ, причём он подходит к осям как угодно близко.
Располагая этими сведениями, мы уже можем соединить точки на рисунке (учитель это делает сам на доске) и увидеть график функции y=12/x целиком. Полученная кривая называется гиперболой, что в переводе с греческого означает «прохожу через что-либо». Эта кривая была открыта математиками древнегреческой школы примерно в 4 веке до н.э. Термин, гипербола ввёл Аполлоний из города Пергам (Малая Азия), живший в ΙΙΙ- ΙΙ в. до н.э.
Теперь рядом с графиком функции y=12/x построим график функции y=-12/x. (Учащиеся выполняют это задание в тетрадях, а один ученик — у доски).
Сравнивая оба графика, учащиеся замечают, что второй занимает 2 и 4 координатные четверти. К тому же, если график функции y=12/x отобразить симметрично относительно оси ОУ, то получится график функции y=-12/x.
Вопрос: Как зависит расположение графика гиперболы y=k/x от знака и от значения коэффициента k?
Учащиеся убеждаются, что если k>0, то график расположен в Ι и ΙΙΙ координатных четвертях, а если k
- Физкультминутку проводит учитель.
- Закрепление изучаемого проходит при выполнении №180, 185 из учебника.
- Подводится итог урока, оценки, задание на дом: п.8 № 179, 184.
2 урок по теме
«Функция обратной пропорциональности и её график».
Выполнила:
Телегина Л.Б.
Цель урока:
- закрепить навык построения графика функции обратной пропорциональности;
- развивать интерес к предмету, логическое мышление;
- воспитывать самостоятельность, внимание.
План урока:
- Проверка выполнения домашнего задания.
- Устная работа.
- Решение задач.
- Физкультминутка.
- Разноуровневая самостоятельная работа.
- Подведение итогов, оценки, задание на дом.
Оборудование: карточки.
Ход урока:
- Учитель объявляет тему урока, цели и план занятия.
Затем двое учащихся выполняют на доске заданные на дом номера 179, 184.
- Остальные учащиеся работают фронтально, отвечая на вопросы учителя.
Вопросы:
- Дать определение функции обратной пропорциональности.
- Что является графиком функции обратной пропорциональности.
- Как зависит расположение графика гиперболы y=k/x от значения коэффициента k?
Задания:
- Среди функций, заданных формулами назвать функции обратной пропорциональности:
а) y=x2+5, б) y=1/х, в) y= 4x-1, г) y=2x, д) y=7-5x, е) y=-11/x, ж) y=x3, з) y=15/x-2.
2. Для функций обратной пропорциональности назвать коэффициент и указать в каких четвертях лежит график.
3. Найти область определения для функций обратной пропорциональности.
(Затем учащиеся карандашом проверяют друг у друга выполнение домашнего задания по проверенному учителем решениям номеров на доске и выставляют оценку).
Фронтальная работа по учебнику № 190, 191, 192, 193 (устно).
- Выполнение в тетрадях и на доске из учебника № 186(б), 187(б), 182.
4. Физкультминутку проводит учитель.
5. Самостоятельная работа даётся в трёх вариантах различной сложности (раздаётся на карточках).
Ι в. (облегчённый).
Постройте график функции обратной пропорциональности y=-6/x с помощью таблицы:
Используя график, найти:
а) значение у, если х = — 1,5; 2;
б) значение х, при котором у = — 1; 4.
ΙΙ в. (средней трудности)
Постройте график функции обратной пропорциональности y=16/x, предварительно заполнив таблицу.
Используя график, найти при каких значениях х у >0.
ΙΙΙ в. (повышенной трудности)
Постройте график функции обратной пропорциональности y=10/x-2, предварительно заполнив таблицу.
Найти область определения данной функции.
(Листы с построенными графиками учащиеся сдают на проверку).
6. Подводится итог урока, оценки, задание на дом: № 186 (а), 187 (а).