Граф с какими свойствами называют деревом
Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
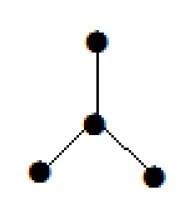
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
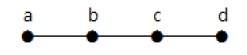
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
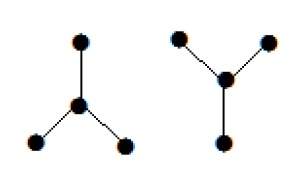
Охватывающие деревья
Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —
- H это дерево
- H содержит все вершины G.
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
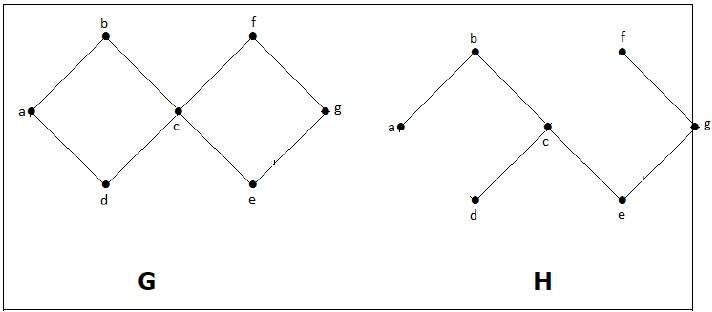
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график —
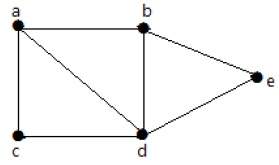
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
Тогда ранг цепи
G = m – (n – 1)
= 7 – (5 – 1)
= 3
пример
Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
n ∑ i = 1 градус (V i ) = 2 | E |
6 × 3 = 2 | E |
| E | = 9
Схема ранг = | E | — (| V | — 1)
= 9 — (6 — 1) = 4
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
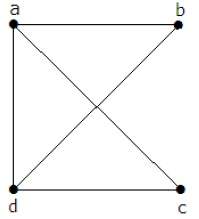
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
2. Назовите элементы, составляющие следующие системы: автомобиль, молекула воды, компьютер, магазин. Солнечная система, семья, футбольная команда, армия. Обоснуйте взаимозависимость элементов этих систем.
Автомобиль: кузов, двигатель, шасси (без чего-либо из этого автомобиль не поедет)
Молекула воды: два атома водорода, атом кислорода (атомы соединены химическими связями)
Компьютер: корпус, системная плата, периферийные устройства (корпус содержит системную плату, к системной плате прикрепляются периферийные устройства)
Магазин: продавцы, товар (продавцы продают товар)
Солнечная система: планеты, спутники планет, Солнце, кометы, астероиды, … (объекты действуют друг на друга гравитацией)
Семья: родители, дети, родственники мужа, родственники жены (все связаны родственными связями)
Футбольная команда: игроки, тренеры, обслуживающий персонал (тренер тренирует игроков, персонал поддерживает игроков, технику, поля в форме)
Армия: военные, оружие, техника (военные управляют оружием и техникой)
3. Что такое граф? Какую информацию он может нести в себе?
Граф — объект, содержащий набор вершин и рёбер, соединяющих вершины. Граф может содержать различную информацию о взаимоотношениях между объектами, например, маршруты между городами, родственные связи, результаты матчей и т.д.
4. Как на графе изображаются элементы системы и отношения между ними?
Элементы системы изображаются вершинами графа, взаимоотношения — рёбрами.
5. Что значит «симметричное отношение», «несимметричное отношение»? Как они изображаются на графе? Приведите примеры.
Симметричное отношение — такое, в котором оба объекта равноценны, т.е. если А находится в отношении с Б, то и Б находится в отношении с А. На графе симметричные отношения неориентированные рёбра и или пары противоположно направленных рёбер. Пример симметричного отношения: быть супругом, быть сестрой, давать в сумме с числом 1000.
Несимметричное отношение — отношение, не являющееся симметричным, на графе обозначается направленными рёбрами. Примеры: влюблённость, отношения порядка (например, «больше»).
6. Дайте имена возможным связям между следующими объектами и изобразите связи между ними в форме графа: брат и сестра; ученик и школа; Саша и Маша; Москва и Париж; министр, директор, рабочий; Пушкин и Дантес; компьютер и процессор.
Брат — сестра (родственники), школа -> ученик (местоположение), Саша — Маша (имена, оканчивающиеся на одинаковые буквы), Москва — Париж (города разных стран), министр -> директор -> рабочий (подчинение), Пушкин <- Дантес (кто умер позже), компьютер -> процессор (входит в состав)
7. Граф с какими свойствами называют деревом? Что такое корень дерева, ветви, листья?
Деревом называют связный граф без циклов. Корень дерева — вершина, не имеющая родителей, ветви — имеющая родителей и потомков, листья — не имеющие потомков.
8. Какие системы называют иерархическими?
Отношения между элементами которых можно представить в виде дерева.
9. Можно ли систему файлов в MS Windows (и ей подобных) назвать иерархической? Какой смысл имеют связи между ее элементами? Что в ней является листьями, ветвями, корнем?
Можно, отношение — «находится в», листья — файлы, ветви — папки, корень — диск или «Мой компьютер»
10. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения):
дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
С Дашей, Маша и Гриша дружат друг с другом и могут проболтаться.
Билет6
1 В теории графов, дерево — связный (ориентированный или неориентированный) граф, не содержащий циклов (для любой вершины есть один и только один способ добраться до любой другой вершины). Древовидная структура — тип организации, в котором каждый объект связан с хотя бы одним другим.
Степень узла — количество поддеревьев узла
Концевой узел (лист) — узел со степенью нуль.
Узел ветвления — неконцевой узел.
Уровень узла определяется рекурсивным образом:
Уровень корня дерева T равен нулю
Уровень любого другого узла на единицу выше, чем уровень корня ближайшего поддерева дерева T, содержащего данный узел.
Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
Ориентированное дерево — это ориентированный граф без циклов, в котором в каждую вершину, кроме одной, называемой корнем ориентированного дерева, входит одно ребро. В корень ориентированного дерева не входит ни одного ребра (входящая степень равна 0). Иногда, термин «ориентированное дерево» сокращают до «дерева».
N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.
Свойства
Дерево не имеет кратных ребер и петель.
Любое дерево с n вершинами содержит n − 1 ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда B − P = 1, здесь B — число вершин, P — число рёбер графа.
Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственным элементарным путём.
Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.
Любое дерево является двудольным графом. Любое дерево, содержащее счётное количество вершин, является планарным графом.
Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.(гамильтонов)
Простой цикл — цикл, не проходящий дважды через одну вершину
Цикл — замкнутая цепь. Для орграфов цикл называется контуром.
Цикл (простой цикл) в орграфе — это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине.
Цикломатическое число графа — число компонент связности графа плюс число рёбер минус число вершин.
2
Чи́сла Фибона́ччи — элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
n | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Fn | -55 | 34 | -21 | 13 | -8 | 5 | -3 | 2 | -1 | 1 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть
, а также ,
где матрицы имеют размер , i — мнимая единица.
- Числа Фибоначчи можно выразить через многочлены Чебышёва:
- Для любого n,
· Следствие. Подсчёт определителей даёт
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример — . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 — x — 1 имеет корни и .
- Отношения являются подходящими дробями золотого сечения φ и, в частности, .
- Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Производящей функцией последовательности чисел Фибоначчи является:
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т.д.
.Рекуррентные соотношения
Последовательность чисел или функций, в которой каждый следующий член выражается через предыдущий, называется рекуррентной, а формулы, устанавливающие эту связь, — рекуррентными соотношениями. Рекуррентные соотношения удобно использовать при составлении алгоритмов вычисления величин, при этом нет необходимости хранить все промежуточные значения. В выражении следующего значения некоторой величины через ее предыдущие значения и состоит суть метода рекуррентных соотношений.
Если последовательность чисел или функций конечна, то для нахождения значений функций (например, суммы, произведения или n-ого члена ) используется арифметический цикл, т.е. цикл, в котором заранее известно число повторений. Трудность при решении таких задач представляет нахождение самой рекуррентной формулы. Я предлагаю ученикам общий подход к получению рекуррентной формулы, опираясь на метод математической индукции.
Вывод рекуррентной формулы
При решении задач на вычисление сумм (произведений) членов конечных или бесконечных последовательностей, вычисления пределов последовательностей наибольшую трудность представляет получение рекуррентной формулы. Далеко не во всех задачах закономерность, связывающая предыдущий и последующий члены последовательности, очевидна, как, например, в последовательности
Любой член последовательности можно выразить как предыдущий умноженный на , т. е. аn+1=аn .
А вот в последовательности
выражение, связывающее следующий член с предыдущим, уже не так очевидно. В таком случае я показываю общую схему получения рекуррентной формулы.
Запишем формулу для любого члена последовательности (2)
Тогда n-ый член последовательности принимает вид:
. Разделим (n+1)-ый член на n-ый.
В результате получим знаменатель последовательности, т.е. тот множитель, который связывает следующий член последовательности с предыдущим.
Следовательно, рекуррентная формула имеет вид
Правильность полученной формулы доказывается индукцией.
Проверим, действительно ли по этой формуле получаем члены последовательности, идущие подряд.
При n=1
При n=2
При n=3 и т.д.
Полученная формула действительно формирует члены последовательности.
4.3. Деревья и лес
Свойства деревьев
Определение 4.12. Граф
называется
деревом, если он связный и не имеет циклов.
Лесом называют граф, связные компоненты которого являются деревьями.
В частности, дерево не может иметь петель и кратных ребер.
Вершину графа, инцидентную только одному его ребру,
называют концевой (или висячей) вершиной,
а ребро, инцидентное концевой вершине, будем называть концевым ребром
графа.
Среди различных деревьев выделяют два важных частных
случая: последовательное дерево, представляющее собой простую
цепь, и звездное дерево (или куст), в котором одна из вершин
(центр) смежна со всеми остальными вершинами.
Пусть множество содержит вершин. Связав эти вершины
ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее
данное множество вершин. Для двух вершин существует одно покрывающее дерево
— сами вершины и ребро, их связывающее. С увеличением
число различных
деревьев быстро
увеличивается:
.
Деревья считаются существенно
различными, если они не изоморфны. Всего деревьев с четырьмя вершинами
16, из них существенно различных только 2; деревьев с шестью вершинами 1296,
а существенно различных всего 6, но уже при насчитывается около миллиона существенно различных
деревьев.. На рис. 4.34 приведены существенно различные деревья с четырьмя и
с шестью вершинами:
Среди графов n-го порядка (с n вершинами) без кратных
ребер полный граф имеет наибольшее количество ребер, а дерево
(n-го порядка) — наименьшее. Дерево содержит минимальное количество
ребер, необходимое для того, чтобы граф был связным.
Теорема 4.9. Каждое
дерево с вершинами
имеет в точности ребро.
► Действительно, две
вершины связываются одним ребром, и для связи каждой добавляемой вершины с
одной из уже имеющихся вершин необходимо еще одно ребро. Если же добавить
два ребра, то есть соединить новую вершину с двумя вершинами, из уже рассмотренных
вершин, то обязательно образуется цикл. Следовательно, для минимальной связи
вершин необходимо
и достаточно ребер. ◄
Нетрудно убедиться в справедливости
следующих теорем.
Теорема 4.10. Граф
является деревом тогда и только тогда, когда каждая пара различных вершин
графа соединяется одной и только одной простой цепью.
Теорема 4.11. У
каждого дерева найдется висячая вершина.
Теорема 4.12. При
удалении любого ребра дерева
оно распадается на связные компоненты, являющиеся либо изолированными вершинами,
либо деревьями. При добавлении в дерево любого нового ребра в нем образуется
простой цикл, и оно перестает быть деревом.
Дерево на рис. 4. 35 при
удалении ребра распадается
на лес из двух деревьев и , а после добавления ребра превращается в циклический
граф .
Рассматриваются также
деревья с ориентированными ребрами (дугами). Ориентированное дерево называется
прадеревом с корнем ,
если существует простой путь между вершиной и любой
другой его вершиной (рис. 4.36). Прадерево может иметь только один корень.
Типы вершин
дерева и его центры
Рассмотрим
дерево с
вершинами. Назовем его
концевые вершины вершинами типа 1. Теперь удалим все вершины типа
1 и концевые ребра. В результате получим связный граф без циклов , то есть опять дерево,
но с уже меньшим количеством вершин. Концевые вершины дерева назовем вершинами типа
2 в дереве .
Аналогично определяются вершины типов 3, 4 и т. д. Легко видеть, что дерево
может иметь либо одну вершину максимального типа, либо две таких вершины.
Типы вершин дерева ,
изображенного на рис. 4. 37, записаны рядом
с соответствующими вершинами. Здесь же показаны последовательные этапы процедуры,
позволяющей их определить. Это дерево имеет две вершины максимального типа.
Если у дерева удалить
одну из вершин типа 2 и ребра, ей инцидентные, то получившееся при этом
дерево будет иметь уже только одну вершину максимального типа.
Пусть вершина типа k
есть вершина максимального
типа. Из определения типа вершин дерева следует, что эксцентриситет
единственной вершины максимального типа равен ее типу, то есть равен
k, а
эксцентриситет каждой из двух вершин максимального типа равен k-1. При этом эксцентриситет
любой вершины не максимального типа будет обязательно больше. Поэтому
центрами любого дерева являются его вершины максимального типа, следовательно,
дерево имеет либо один, либо два центра. Нетрудно убедиться, что диаметральные
цепи в деревьях проходят через его центр или через оба центра, если
их два. В первом случае длина диаметральной цепи равна
2k-2, а во втором 2k-1.
