Что такое объем и какими свойствами он обладает

Данный урок посвящён важному математическому понятию – объему тела. Это одна из главных величин, связанная с геометрическими телами, она измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. В уроке будут названы основные свойства объёма тела. Вы узнаете, что такое «аддитивность», разберётесь в доказательстве важнейшего следствия, которое будет использоваться при доказательстве формул объёма параллельного параллелепипеда и призмы.
Введение
Рис. 1. Примеры, в которых речь заходит об объеме
Сколько воды нужно, чтобы наполнить бассейн? Сколько сока поместится в кружке? И как определить, золотая корона или нет? (См. Рис. 1.)
Все это и многое другое относится к понятию объема.
Всегда при изучении такой темы возникают сложности: все и так понимают, что такое объем, ведь понятие объема появляется еще в начальной школе… Но проблема в том, что тогда всё формулировалось исключительно на интуитивном уровне. Например, объем стакана – это сколько воды в нем поместится или объем комнаты – сколько в ней воздуха.
Теперь мы можем ввести строгое определение и в соответствии с ним вывести заново некоторые уже известные формулы, а заодно доказать неизвестные.
Рассказ про Архимеда и Эврику
Однажды сиракузский царь Гиерон II поручил своему ювелиру изготовить золотую корону. После изготовления сего абсолютно необходимого для царей предмета в голову Гиерону закралась естественная для руководителя мысль: «А не обманул ли меня мой ювелир? Не подмешал ли он в корону значительную часть серебра вместо золота и не прибрал ли ювелир золото к рукам?»
Проверить это было поручено Архимеду. Нужно было выяснить, содержит ли корона серебро вместо золота, не разрушая при этом само ювелирное изделие. Поиски истины были трудны, над составом сплава великий математик трудился долго и безуспешно, пока, наконец, случайно, во время купанья, погруженный в мысли о вычислении объема сложного тела, Архимед погрузил свое тело в воду… и решение задачи было найдено.
Легенда гласит, что Архимед пришел в полный восторг от этого открытия и голый с криком: «Эврика!» побежал из купальни, чтобы проверить свою теорию.
Великий математик пришел к Гиерону II и попросил предоставить ему слиток золота и слиток серебра точно такого же веса, что и корона. Потом он наполнил доверху сосуд и положил в него слиток серебра. Вполне понятно, что каков был объем серебряного слитка, такое количество воды и вытекло.
Затем, вынув слиток, он долил в этот сосуд точное количество вытесненной воды, измеряя этот объем секстарием. Таким образом, Архимед определил, какой вес серебра соответствует какому количеству воды.
Затем, он опустил золотой слиток в сосуд и тем же способом, при помощи секстариев, великий математик выяснил, насколько меньший объем занимает слиток золота по сравнению со слитком серебра аналогичного веса.
После чего, опять наполнив сосуд и опустив в него корону, Архимед определил, что при погружении короны вытекло больше воды, чем при погружении в сосуд золотой массы того же веса.
Заключение Архимеда было следующим. Так как короной вытеснялось большее количество воды, чем золотым слитком, то в золоте, из которого изготовлена корона, содержится примесь серебра.
Что стало с ювелиром, история умалчивает.
Аналогия с понятием площадь
Рис. 2. Площади фигур на плоскости
Понятие объема в пространстве аналогично понятию площади на плоскости. В курсе планиметрии говорилось, что у каждой фигуры на плоскости есть площадь – положительная величина, которая определяет, сколько места занимает данная фигура на плоскости (см. Рис. 2).
Свойства площади
1. Площадь – величина положительная: .
Рис. 3. Равные фигуры
2. Равные фигуры (см. Рис. 3) имеют равные площади: .
Рис. 4. Фигура из нескольких
3. Если фигура состоит из нескольких частей (см. Рис. 4), то ее площадь равна сумме площадей этих частей: .
Рис. 5. Квадрат со стороной 1
4. Площадь квадрата (см. Рис. 5) равна квадрату его стороны: (для квадрата со стороной ).
Аналогичными свойствами обладает и объем.
Понятие объема
Рис. 6. Ящик объемом 1
Объемом фигуры в пространстве называется положительное число, соответствующее количеству места, занимаемое фигурой в пространстве. Иначе говоря, объем – это такая функция, которая ставит в соответствие каждой фигуре некоторое положительное число, и это число показывает, сколько места в пространстве занимает фигура.
Понятно, что число это без выбора единицы измерения ничего не значит. Например, если объем ящика равен , то он большой или маленький (см. Рис. 6)?
Если , то большой (см. Рис. 7), а если , то размером с спичечный коробок (см. Рис. 8).
Так что перед тем как говорить о числе, необходимо задать единицу измерения (, , и т. д.)
Рис. 9. Куб со стороной 1 см
Почему кубические? Потому что мы будем отталкиваться от куба, то есть все фигуры будем представлять через объем куба. Соответственно, если у куба была сторона см (см. Рис. 9), то его объем будет равен одному кубическому сантиметру: .
Рис. 10. Коробка объемом
Тогда дальше мы будем пытаться понять, из скольки кубиков состоит какая-либо заданная фигура. Например, если взять коробку, которую можно заполнить кубиками, каждый из которых имеет объем , ее объем будет равен (см. Рис. 10).
Объем измеряется не только кубическими единицами, а еще и литрами, галлонами, пинтами, баррелями и так далее, но они не являются базовыми.
Можно измерять не только «кубиками», но и другими объектами, например «бочками» или «кружками» и т. д. Просто кубиками (и вообще прямоугольными параллелепипедами) можно приблизить фигуру сколь угодно точно – поэтому чаще используют именно «кубики».
Предположим, что есть фигура, объем которой равен кубическим сантиметрам. Это значит, что фигура состоит из двух кубиков, каждый из которых имеет объем . Причем фигура не обязательно должна иметь вид двух стоящих рядом или друг на друге кубиков, но тем не менее она должна занимать столько же места в пространстве, сколько в сумме занимают два кубика со стороной см. Обозначается это так: .
Система мер
Удобно, когда везде единые системы обозначения. Если, например, один магазин продает воду литрами, другой – кубическими сантиметрами, третий – пинтами ( пинта литра), то как сравнить, где выгоднее? Можно все свести к одной единице измерения, но это довольно долго и неудобно. С другой стороны, не все удобно измерять в тех же литрах: скажем, нефть обычно измеряют в баррелях, так как, во-первых, получается меньшее число ( баррель литров). Тем не менее, люди стараются одни и те же вещи измерять одинаково: напитки – литрами, материалы (песок, цемент) – кубометрами, нефть – баррелями и т. д. Очень многое зависит и от страны проживания. Так, например, в Британии объем жидкостей чаще измеряется пинтами, у нас – литрами.
Приближенное вычисление площади
Рис. 11. Площадь
Как разбить фигуру на кубики? На самом деле, в качестве аналогии можно вспомнить, как площадь подграфика функции заполняется прямоугольниками (См. Рис. 11).
Рис. 12. Заполнение фигур пространства маленькими
Так мы задавали определенный интеграл. Аналогично заполняются и фигуры в пространстве (см. Рис. 12). Так мы приблизим объем данной фигуры к сумме объемов маленьких кубиков.
Буква V в геометрии
Вы уже привыкли, что объем обозначается буквой , но почему именно это буква? Площадь обозначают от слова Square (площадь). А объем?
Буква в данном случае значит Volume, то есть с латинского – «объем», «наполнение».
Свойства объема
Рис. 13. Равные фигуры
1. Равные фигуры (см. Рис. 13) имеют равные объемы: .
Рис. 14. Пакет молока и кубик одинакового объема
Обратное неверно. Объем может быть одинаков и при разной форме. Например, литровый пакет молока имеет тот же объем, что и кубик со стороной дм (, но фигуры не равны (равными называют, как и на плоскости, те фигуры, которые совмещаются при наложении) (см. Рис. 14).
Рис. 15. Фигура из 3 кубиков
2. Если некоторое тело в пространстве составлено из нескольких тел (без наложений) (см. Рис. 15), то объем исходного тела равен сумме объемов тех тел, из которых оно составлено: .
Сформулированные два свойства обычно называют основными свойствами объемов.
Кроме этого иногда выделяют отдельно третье свойство.
3. Объем единичного куба равен единице: .
Рис. 16. Единичный куб
Эти три свойства нами не доказаны – и доказаны не будут: как и в случае с площадями, они сформулированы как аксиомы объема, а затем уже на их базе будем абсолютно строго выводить различные формулы.
Следствия из третьего свойства
Рис. 17. Куб со стороной
Следствие 1. Объем куба со стороной (см. Рис. 17) равен : .
Доказательство. Пусть , (см. Рис. 18).
Рис. 18. Сторона куба равна
Разобьем куб на маленькие кубики со стороной 1. Раз , то каждая сторона разобьется на частей (см. Рис. 19).
Рис. 19. Разбиение куба на маленькие
Найдем количество кубиков. Очевидно, что слоев будет (см. Рис. 20).
Рис. 20. Разбиение куба на слоев
В каждом слое помещается кубиков. Значит, всего кубиков будет . Объем каждого из них равен 1 (по третьему свойству). Тогда объем всего куба равен (по второму свойству). Имеем, . Что и требовалось доказать.
Следствие 2. Объем куба со стороной () равен :
Рис. 21. Единичный куб
Доказательство. Пусть . Рассмотрим единичный куб (см. Рис. 21).
Рис. 22. Разбиение единичного куба плоскостями
Разобьем его плоскостями (как в следствии 1), а каждую сторону на частей. Соответственно, если сторона равна 1, то каждый образовавшийся отрезок равен (см. Рис. 22).
Количество кубиков, которые помещаются в куб, будет равно . Но объем каждого из них неизвестен, а известен лишь объем большого куба (по третьему свойству). Учитывая то, что единичный куб состоит из маленьких одинаковых кубиков, чьи объемы равны (по первому свойству), то общий объем равен . Тогда . Что и требовалось доказать.
Следствие 3. Объем куба равен кубу его стороны: .
Объем единичного куба. Доказательство Следствия 3
Разберем 3 случая.
— Если сторона куба – натуральное число (, ). Тогда мы получаем следствие 1, которое уже было доказано ранее.
Рис. 23. Разбиение куба на частей
— Если сторона куба – дробное число. Пусть ; . Разобьем каждую сторону на частей. Получаем кубиков, сторона каждого из которых равна (см. Рис. 23).
А тогда объем каждого маленького кубика (по следствию 2). Тогда искомый объем . Что и требовалось доказать.
— Если сторона куба – произвольное вещественное число. Рассмотрим 2 последовательности, они будут строиться следующим образом. Сначала возьмем два соседних целых числа, между которыми заключено число (сторона куба): , . Теперь оценим с точностью до десятых , где . Теперь оценим до сотых , где и т. д.
Соответственно, объем куба со стороной будет больше, чем объем куба со стороной , и меньше, чем объем куба со стороной : , где (; ; ; ; ; и т. д). Если устремить к бесконечности, то мы получим, что левая и правая часть неравенства сколь угодно близки, то есть и стремятся к одному и тому же числу. Таким образом, если перейти к пределу, то получим, что , то есть . Что и требовалось доказать.
Заключение
На этом уроке было введено понятие объема, выяснено, какими свойствами обладает объем, и сформулировано важное следствие . В дальнейшем из полученных свойств и следствий мы выведем формулы объемов для основных фигур в пространстве.
Список литературы
- Геометрия. Учебник для 10–11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
- В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Uztest.ru (Источник).
- School-collection.edu.ru (Источник).
- Yaklass.ru (Источник).
Рекомендованное домашнее задание
- Сколько литров воды вмещает бак, имеющий форму куба с ребром дм?
- Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
- Площадь поверхности куба равна . Найдите его объем.
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Понятие объема
Понятие объема
Подобно тому, как для фигур на плоскости вводится понятие площади, для тел в пространстве вводится понятие объема. Сначала рассмотрим только простые тела. Тело называется простым, если его можно разбить на конечное число треугольных пирамид.
Для простых тел объем — это положительная величина, численное значение которой обладает следующими свойствами:
1. Равные тела имеют равные объемы.
2. Если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей.
3. Объем куба, ребро которого равно единице длины, равен единице.
Если куб, о котором идет речь в определении, имеет ребро 1 см, то объем будет в кубических сантиметрах; если ребро куба равно 1 м, то объем будет в кубических метрах; если ребро куба равно 1 км, то объем будет в кубических километрах и т. д.
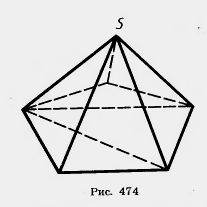
Примером простого тела является любой выпуклый многогранник. Его можно разбить на конечное число треугольных пирамид следующим образом. Отметим какую-нибудь вершину S многогранника. Разобьем на треугольники все грани многогранника, не содержащие вершину S. Тогда треугольные пирамиды, для которых основаниями являются эти треугольники, а общей вершиной — точка S, дают разбиение многогранника на На рисунке 474 показано такое разтреугольные пирамиды биение для произвольной пирамиды.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
![]() конспект урока
конспект урока
![]() опорный каркас
опорный каркас
![]() презентация урока
презентация урока
![]() акселеративные методы
акселеративные методы
![]() интерактивные технологии
интерактивные технологии
Практика
![]() задачи и упражнения
задачи и упражнения
![]() самопроверка
самопроверка
![]() практикумы, тренинги, кейсы, квесты
практикумы, тренинги, кейсы, квесты
![]() домашние задания
домашние задания
![]() дискуссионные вопросы
дискуссионные вопросы
![]() риторические вопросы от учеников
риторические вопросы от учеников
Иллюстрации
![]() аудио-, видеоклипы и мультимедиа
аудио-, видеоклипы и мультимедиа
![]() фотографии, картинки
фотографии, картинки
![]() графики, таблицы, схемы
графики, таблицы, схемы
![]() юмор, анекдоты, приколы, комиксы
юмор, анекдоты, приколы, комиксы
![]() притчи, поговорки, кроссворды, цитаты
притчи, поговорки, кроссворды, цитаты
Дополнения
![]() рефераты
рефераты
![]() статьи
статьи
![]() фишки для любознательных
фишки для любознательных
![]() шпаргалки
шпаргалки
![]() учебники основные и дополнительные
учебники основные и дополнительные
![]() словарь терминов
словарь терминов
![]() прочие
прочие
Совершенствование учебников и уроков
![]() исправление ошибок в учебнике
исправление ошибок в учебнике
![]() обновление фрагмента в учебнике
обновление фрагмента в учебнике
![]() элементы новаторства на уроке
элементы новаторства на уроке
![]() замена устаревших знаний новыми
замена устаревших знаний новыми
Только для учителей
![]() идеальные уроки
идеальные уроки
![]() календарный план на год
календарный план на год
![]() методические рекомендации
методические рекомендации
![]() программы
программы
![]() обсуждения
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Геометрия, 11 класс
Урок №11
Понятие объёма
Перечень вопросов, рассматриваемых на уроке:
Понятие объёма.
Свойства объёмов.
Объём прямоугольного параллелепипеда.
Формула объёма прямоугольного параллелепипеда.
Тезаурус
Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.
Основные свойства объёма:
— равные тела имеют равные объёмы;
— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Основная литература:
Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.
Теоретический материал для самостоятельного изучения
С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.
Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.
Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.
Объём обозначается заглавной латинской буквой V.
Пример:
Объём книги400 кубических сантиметров запишут: V = 400см3.
Рассмотрим свойства объёмов.
Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Следствие из основных свойств объёмов.
Объём куба с ребром 1/n равен 1/n3
Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см3). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n3.
Объём прямоугольного параллелепипеда
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Доказательство
Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.
Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.
Случай второй.
Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: an, bn, cn, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, an ≤ a ≤ an’, где an’ = an+1 : 10n. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение anbncn ≤ abc ≤ an’bn’cn’, где bn’= bn+1 : 10n, cn’ = cn+1 : 10n
По доказанному в первом случае, левая часть неравенства представляет собой объём Vn прямоугольного параллелепипеда Pn с измерениями an, bn, cn, а правая часть – это объём Vn’ прямоугольного параллелепипеда Pn’ с измерениями an’, bn’, cn’. Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Примеры и разбор решения заданий тренировочного модуля.
№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
 №2.
№2.
Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см3, AB = 8 см, АА1= 20 см.
Варианты ответов:
220 см2
100 см2
400 см2
200 см2
Решение.
Найдём длину АD:
AD = 960 : 8 : 20 = 6 см
Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.
Ответ: площадь закрашенной фигуры 200 см2.
Верный ответ: 200 см2.
