Что такое идеальный газ какими свойствами он обладает

Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма — частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
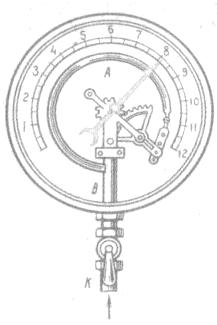
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
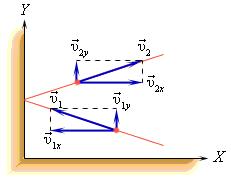
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
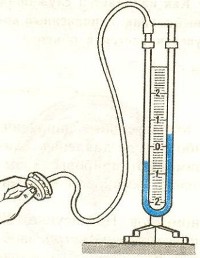
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый — для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

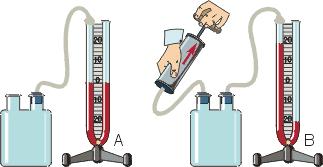
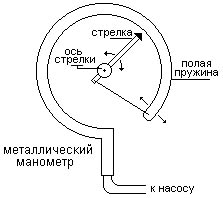
Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 — масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 — средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
![]()
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим ![]() или
или ![]()
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
![]()
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
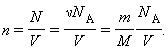
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
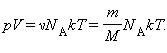
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
![]()
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Анна Кустова · 22 декабря 2016
14,5 K
Физик-теоретик, PhD студент в Университете Уппсалы, Швеция
На этом примере мы можем детально рассмотреть, как математические модели трансформируются в физические модели.
Прежде всего, идеальный газ — это математическая модель газа. И с математической точки зрения, идея очень проста: атомы (или молекулы) этого самого газа «не видят» друг друга. То есть каждая частица воспринимает сосуд как совершенно пустой. Такие частицы могут проходит друг сквозь друга. Из этого следует, например, что все частицы могут собраться в одной пространственной точке.
С другой стороны идеальный газ — это физический термин. А значит, нам надо понять, какая физика отвечает такой математической модели.
а) Итак, во-первых, чтобы атомы «не видели» друг друга надо чтобы между ними не было потенциальных сил взаимодействия, то есть сил зависящих от расстояния между частицами. В терминах энергии это требование звучит так: » потенциальная энергия взаимодействия частиц равна нулю». Такое строгое равенство нулю, это все еще математика, в физике мы можем смягчить это условие, сказав «потенциальная энергия взаимодействия частиц много меньше …». Чего? Энергию можно сравнивать только с энергией, а системе движущихся частиц наибольший вклад дает кинетическая энергия. И вот наше первое условие:
1) Потенциальная энергия взаимодействия частиц газа много меньше их кинетической энергии.
б) В математической модели молекулы представляются математическими точками, то есть без размера. В реальном мире такого требовать мы не можем. Как же нам сформулировать это условие физически? Зачем нам безразмерные молекулы? Для того чтобы они не сталкивались друг с другом. Мы не можем запретить соударение частиц ненулевого размера без ввода в систему сил отталкивания. Но силы отталкивания мы исключили первым пунктом. Тогда нам придется разрешить столкновения в системе, но с наложением 3 условий: редко, быстро и без потерь энергии. И вот еще 3 пункта:
2) Средняя длина свободного пробега частиц (то есть расстояние проходимое между двумя последовательными столкновениями) много больше их размера.
3) Время столкновения пренебрежимо мало.
4) Все столеновения происходят без потерь энергии.
Пункты 3) и 4) мы распространим и на соударение со стенками сосуда. Если все четыре требования выполнены, то мы можем считать наш газ идеальным.
в) Еще одна интересная деталь. Кое-что наши столкновения в систему все же вносят. А именно, изменения скоростей. Причем модуля и направления. Так что какое бы распределение скоростей не было в самом начале, после множества столкновений они уже будут распределены по Максвеллу. По этому, строго говоря, нам надо потребовать, чтобы уже изначально распределение скоростей было таким. Тогда наши столкновения не будут влиять на изначальную физику системы:
5) Частицы в системе имеют случайные скорости, распределенные по закону Максвелла.
В неявном виде мы уже потребовали применимость закон Ньютона в системе (для закона сохранения импульса, например):
6) В системе действуют законы Ньютона.
Последний пункт всегда подразумевается, так что его можно опустить. А предпоследний можно опустить, так как система сама придет к нему, если первые четыре пункта выполнены.
Но! Если вы будете моделировать идеальный газ на компьютере, например, и захотите сделать его математически идеальным, т.е. без столкновений, то вам необходим пункт 5)! Иначе вы не получите правильной физики. И наоборот, если вы будете моделировать физическую систему, т.е. в соотвествии с первыми четырьмя пунктами, то как я писала ранее, через какое-то время система сама придет к пункту 5).
Вы всё очень хорошо описываете и мне нравятся ваши ответы , но мне кажется можно было бы привести в пример… Читать дальше
Идеальным называют газ размерами молекул которого и взаимодействием между ними можно пренебречь . Большинство газов вплоть до давления приблизительно 10 атм. можно рассматривать как идеальные. Создана данная идеальная абстракция для упрощения расчётов и выделения основных параметров таких как давление , объём , температура .
Так же думаю стоит… Читать далее
Если очень просто, то это упрощенное видение любого газа, используемое для расчета. Все объекты, что находятся в материальном мире, испытывают воздействия многочисленных сил и являются участниками многочисленных процессов. Однако большая часть этих сил и процессов оказывают слишком малое влияние на состояние объекта и если перед физиком не стоит… Читать далее
Объясните принцип неопределённости Гейзенберга простыми словами?
Не устроили меня предыдущие ответы. Попытаюсь объяснить принип неопределенности простыми словами и без формул.
1) Принцип неопределенности не связан с процессами измерений. Хотя для его доказательства, естественно, необходимо производить опыты и измерения.
2) Я считаю, что лучше всего его можно понять, рассматривая волны де Бройля — волны вероятности (или амплитуды вероятности). Т.к. в этом случае исключаются всякие спекуляции, которые приводят к зависимости поведения физической системы от состояния наблюдателя. Но и здесь, конечно, существует оговорка. Если наблюдатель действует достаточно грубо (к примеру, в известном двухщелевом эксперименте, подсматривая за частицей), то воздействием измерительного прибора пренебречь нельзя. И здесь лучше ознакомиться с таким понятием, как «слабое измерение», что не является темой нашего исслелования.
Иными словами, произведенные измерения влияют на поведение квантовой системы всегда ПОСЛЕ измерений, и никогда ДО.
Рассмотрим принцип неопределенности для координат и импульсов частицы.(Хотя принцип неопределенности существует и для других сопряженных физических величин).
Согласно гипотезе де Бройля, описание поведения частицы можно проводить рассматривая некие волны-волны вероятностей.(так можно говорить и о пси-функции). Квантовая механика говорит о том, что поведение частицы не является определенным(детерменированным), а вот вероятности, напротив, вполне детерменированы(подчиняются ур.Шредингера).
Если частица(ее поведение) есть волновой процесс, то для математического описания необходимо использовать некую периодическую функцию(в принципе, любую). А что же будет аргументом этой функции? Конечно время. Но нам оно сейчас не понадобится. А что еще? Еще — наверное, координата. Но просто так мы не можем записать ее в качестве аргумена. Аргумент должен быть безразмерным! Значит есть еще какая-то физическая величина с размерностью обратной координате, на которую домножим координату. Эта величина называется волновым вектором. И тоже является характеристикой волны. Таким образом волна(любая!) описывается координатой и сопряженной величиной — волновым вектором (впомните, это так же как частотой и временем. И тут же забудьте, т.к. это сейчас неважно).
Теперь вернемся опять к нашей частице(и ее поведению). Она не может быть представлена просто в виде волны(хотя бывает). Т.к. волна, вообще говоря бессконечна в пространстве. А про частицы мы знаем, что где-то они все-таки находятся (где-то в пространстве вероятность их обнаружения больше). Поэтому для описания частицы нам подойдет такой объект как «волновой пакет». А как мы можем его соорудить. Здесь нам приходит на помощь преобразования Фурье, которое говорит, что волновой пакет можно составить из нескольких волн, с немного различающимися волновыми векторами. Обратите внимание: волновой пакет — это цельный объект у которого физическая величина «волновой вектор» как бы немножко размазана (неточно определена). Но и точной координаты у волнового пакета нет — у него есть некая ширина. И тут оказывается, что если мы умножим ширину неопределенности волнового вектора на ширину неопределенности координаты, то мы получим ровно 2 пи.
Но тут есть один подвох. Мы же складывали волны простирающиеся в бесконечность. А получили конечный волновой пакет. И должны понимать, что это не совсем так. Даже за пределами пакета колебания тоже будут, но очень маленькие. Поэтому вместо равенства двум пи, мы дожны написать знак больше либо равно.
А в квантовой механике импульс частицы есть волновой вектор (умноженный на постоянную Планка, деленную на 2 пи). Отсюда мы и получаем соотношение неопределенности.
Вот так это выглядит при простейшем рассмотрении. Да, константы немного будут отличаться от более точного вычисления в квантовой механики для среднеквадратичных отклонений. Но это совсем не принципиально.
Частица определяется только своим поведением и ничем больше — это поведение недетеминировано (вероятно) — вероятности же напротив вполне определены (детерменированы) — средние значения сопряженных физических величин, описывающих поведение частицы подчиняются принципу неопределенности.
Прочитать ещё 4 ответа
Объясните мне простым языком, что такое «теория Эфира»?
физик-теоретик в прошлом, дауншифтер и журналист в настоящем, живу в Германии
Существование «эфира» (или нескольких разных «эфиров») — это физическая ГИПОТЕЗА, которая в конечном итоге НЕ ПОДТВЕРДИЛАСЬ. Сам эфир — это невидимая и неощутимая обычными способами субстанция, которая, якобы, заполняет все пространство (или, как вариант, ту часть пространства, где нет обычного вещества).
Идею эфира использовали по следующим причинам (одной, или нескольким сразу):
- из-за умозрительной философской идеи, что в природе, якобы, не бывает абсолютной пустоты;
- как особую субстанцию, служащую для передачи дальнего взаимодействия (например, гравитационного) через незаполненное веществом пространство;
- как особую субстанцию, изменение свойств которой, влияет на распространение частиц света в корпускулярной его теории и помогает объяснить некоторые эффекты (дифракцию и преломление света, например);
- как особую субстанцию, колебания которой (продольные, или поперечные) являются электромагнитными волнами (и светом, в частности) — наподобии того, как колебания обычного вещества порождают механические волны.
Иногда предполагалось существование разных видов эфира — для объяснения разных эффектов, взаимодействий и волн.
От идеи эфира отказались из-за ее непродуктивности: все реально наблюдаемые явления удалось объяснить другими способами, а ожидаемые следствия «существования» эфира («эфирный ветер», например) не удалось экспериментально обнаружить.
- По п. 1 — не было никаких реальных причин верить в эту идею за рамками взаимодействий и/или волн.
- По п. 2 — так и не была создана сколь-нибудь внятная и продуктивная (предсказывающая какие-то новые экспериментально-подтвержденные эффекты) теория гравитационного взаимодействия посредством «эфира». Эйнштейновская ОТО (общая теория относительности) объяснила природу гравитации иным способом (без эфира), а противоречия ОТО с квантовой физикой не устраняются возрождением идеи эфира.
- По п. 3 — эфир помогал устранить проблемы классической корпускулярной теории света с объяснением явлений дифракции и преломления, дополняя теорию идеей о разной плотности эфира в разных областях пространства. Мол, плотность эфира влияет на скорость движения корпускул — отсюда разная скорость света в разных веществах (а разная скорость ведет к преломлению на границе раздела). И дифракция, мол, тоже связана с переменной плотностью эфира и обусловленной ею переменной скоростью корпускул. Но после открытия явления интерференции света, корпускулярная теория умерла, а ее «эфирный» костыль стал ненужен.
По п. 4 — эфир сначала был «нужен» теоретикам как носитель «волны» света. После объяснения электромагнитных волн на основе уравнений Максвелла, эта нужда отпала. Зато эфир стали «прилаживать» для объяснения преобразований Лоренца в классическрй электродинамике, позволяющих изменять систему координат без изменения вида уравнений Максвелла. Мол, это эфир имеет такие свойства и так влияет на свет, что КАЖЕТСЯ, будто расстояния и время становятся для света относительными. Создание эйнштейновской СТО (специальной теории относительности: это как ОТО без искривления пространства-времени и без гравитации) сделало гипотезу «эфира» ненужной и в этой роли: в разных системах отсчета расстояния и время ДЕЙСТВИТЕЛЬНО отличаются — и не только для электромагнитных волн, а для всех объектов.
Итак, эфир стал не нужен для ОБЪЯСНЕНИЯ чего-либо. Но, может, он на самом деле все же существует «сам по себе»? Увы, но не удалось обнаружить никаких прямых доказательств взаимодействия эфира с веществом или электромагнитным полем. Значит, «эфир» не взаимодействует ни с чем реально существующим и его нельзя приспособить для «объяснения» чего-то необъясненного другими способами, более логичными и продуктивными (уравнения Максвелла, СТО, ОТО). Так зачем он нужен и почему в его существование надо верить? Если нечто (эфир, или бог, или гипотетический чайник_Рассела на околосолнечной орбите, например) никак себя не проявляет, значит этого нечто, скорее всего, вообще не существует.- *
Зато определенный АНАЛОГ покойного «эфира» позже появился в квантовой теории поля. Только это уже не нечто вовсе неведомое, (не «эфир»), а все те же элементарные частицы (фотоны, электроны, позитроны и прочие), но ВИРТУАЛЬНЫЕ (возникающие на короткое время из ничего — в нарушение закона сохранения энергии — и почти сразу же исчезающие). Как и «эфир» виртуальные частицы, наполняющие все пространство, невозможно НАПРЯМУЮ наблюдать. Как и эфир, они служат переносчиком взаимодействия (причем всех видов взаимолействий, или — почти всех видов, кроме — возможно — гравитационного) Но, в отличие от эфира, гипотеза существования виртуальных частиц не просто задним числом позволила кое-что объяснить, но и предсказала множество новых эффектов, большинство которых ПОДТВЕРЖДЕНЫ экспериментально. (Последним по времени стало рассеяние фотонов на фотонах, экспериментально зарегистрированное только в этом году, а теоретически предсказанное аж 70 лет назад!) Поэтому нет оснований особо сомневаться в РЕАЛЬНОСТИ этих «виртуальных» частиц.
Прочитать ещё 6 ответов
Что такое физика?
Сусанна Казарян, США, Физик
Физика это язык на котором общаются физики. Грамматикой этот язык не отличается от обычного языка общения людей, но у нормального человека (не-физика), даже пол-часа проведенные на семинаре по теоретической физике, вызывает непроизвольную зевоту и последующий сон. В случаях же головной боли или головокружения, обычно советуют обратиться к парапсихологу.
Прочитать ещё 1 ответ
Есть утверждение, что Вселенная постоянно расширяется. А куда она расширяется? Что за границей Вселенной?
75 лет, ХГУ , астроном, учитель,пенсионер.
Если представить себе двумерное пространство в виде резинового листа, а на него положить тяжелый шар — то лист прогнется.
Но в области прогиба плоской Вселенной от гравитирующей массы пространство уже не плоская двухмерная поверхность, это уже трехмерная сферическая поверхность! Гравитирующая масса вещества воздействует на окружающее пространство преврашая его в n+1 пространство. Если продолжить в центре наращивать массу тела — эта масса начнет все больше сворачивать пространство в сферу
Мы получили сферу из плоскости. И если раньше равнодействующая на все тела была равно нулю, то на поверхности сферы на каждую точку будет направлена в центр сферы.
Так что ответ на ваш вопрос таков — вселенная будет расширятся в центр сферы, пока сфера не превратится в шар. Внутрь расширятся будет а не наружу как вы думаете, и как думают остальные.
А поскольку наша Вселенная трехмерная , то она расширяется в четвертое измерение пространства, которое мы пока не видим и не воспринимаем. Пока не видим.
Прочитать ещё 4 ответа
Объясните, пожалуйста, первый закон Рауля простыми словами?
Researcher, Institute of Physics, University of Tartu
Значит так, во-первых, мы имеем дело с парами, которые описываются моделью идеального газа. Как известно, давление идеального газа при данной температуре зависит только от его мольного количества, но не от состава. То есть, давление (1 моля газа А) = давление (0.5 моля газа А + 0.3 моля газа Б + 0.2 моля газа В).
Теперь перейдем к жидкостям. Над любой жидкостью есть некоторое давление пара, равновесное при данной температуре. Мы считаем эти пары идеальными газами (см. выше). Тогда первый закон Рауля гласит, что равновесное давление паров смеси нескольких жидкостей будет равно сумме равновесных давлений паров каждого компонента этой смеси, домноженного на мольную долю этого компонента в смеси. То есть, представим себе что у нас есть жидкость А с равновесным давлением паров Ра, жидкость Б с равновесным давлением паров Рб и жидкость В с равновесным давлением паров Рв. Если они взяты в чистом виде, то равновесное давление паров над ними будет равно 1*Ра, 1*Рб и 1*Рв, соответственно, поскольку доля жидкости в чистой жидкости равна 1.
Теперь возьмем смесь — 0.5 жидкости А, 0.3 жидкости Б и 0.2 жидкости В. Тогда общее давление паров (не забываем про идеальность! см. начало, если забыли) над этой смесью (раствором) будет равно: Робщ. = 0.5*Ра + 0.3*Рб + 0.2*Рв. Вот и всё. Это означает, что если в какой-то смеси, например, 99.9% нелетучего компонента и 0.1% летучего, то суммарное давление все равно будет почти как у нелетучего, несмотря, что, может, у летучего давление паров в 10 раз выше, чем, у нелетучего.
Соблюдается первый закон Рауля не очень часто, я бы сказал. Это должны быть достаточно близкие по химической природе жидкоти, они не должны давать заметных тепловых эффектов и заметного изменения объема при смешении, они не должны быть слишком полярные и т.д. и т.п. Но в целом как не очень точное приближение он хорошо работает в большинстве случаев.
